※ 2016.07.27追記
もう少し複雑なサンプルを使った解析と、
ここで使われているダーバージェンスという情報量に関する記事を追加しました。
0. 前振り
言葉の解析をしたい。
ある文章と、ある文章は近いか?という距離を測りたい。
対象となるデータは離散化された「文字」が「順序」を持って並んでいるとする。
ここでは、「遷移確率」を考える。
このページの例をパクると、
- いちごじゃむを食べる。
- いちごが好き。
- いちごのジャムを作る。
この3文の中で、「い」と「ち」と「ご」の出現数は同一であるが、
「い→ち」遷移確率:100%
「ち→ご」遷移確率:100%
「ご→を」「ご→が」「ご→の」遷移確率:33%
という事になっている。
つまり、文節や単語の切れ目では遷移確率が下がる。
文字列から遷移確率を出し、文字列間の距離を定量してクラスタ化できるだろうか?
1. サンプルデータ
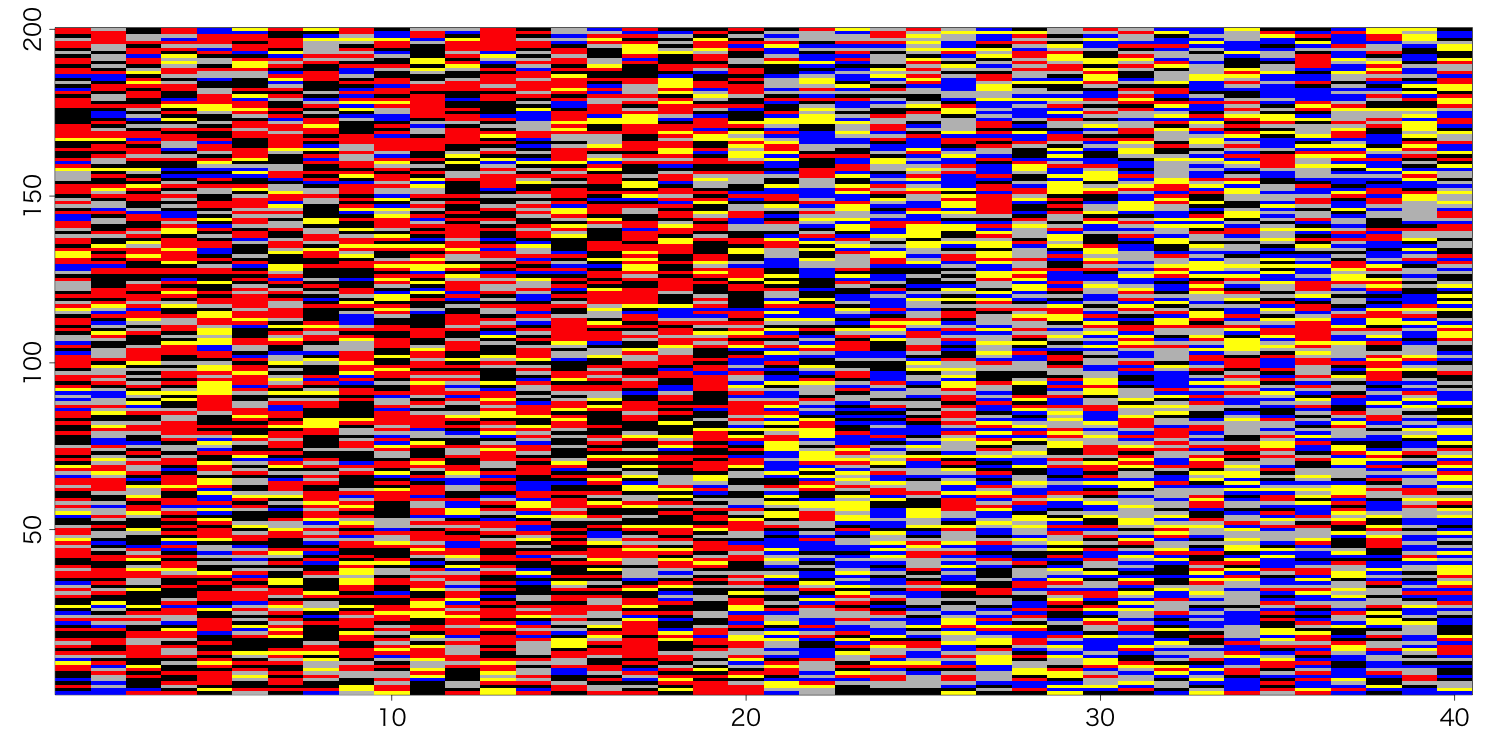
5つの文字(A, B, C, D, E)からなる文字列を考える。
文字には色を与えておく。

これを1カラムとして、40サンプルを横に並べる。
ただし、最初の20サンプルと、後の20サンプルでは、語の出現頻度を偏らせておく。
set.seed(1)
dat <- NULL
for(i in 1:20){
dat <- cbind(dat, sample(c(1:5, 2, 4, 4, 4, 5, 5), 200, replace = T))
}
for(i in 1:20){
dat <- cbind(dat, sample(c(1:5, 1:5, 2, 3), 200, replace = T))
}
2. 遷移確率マトリックス
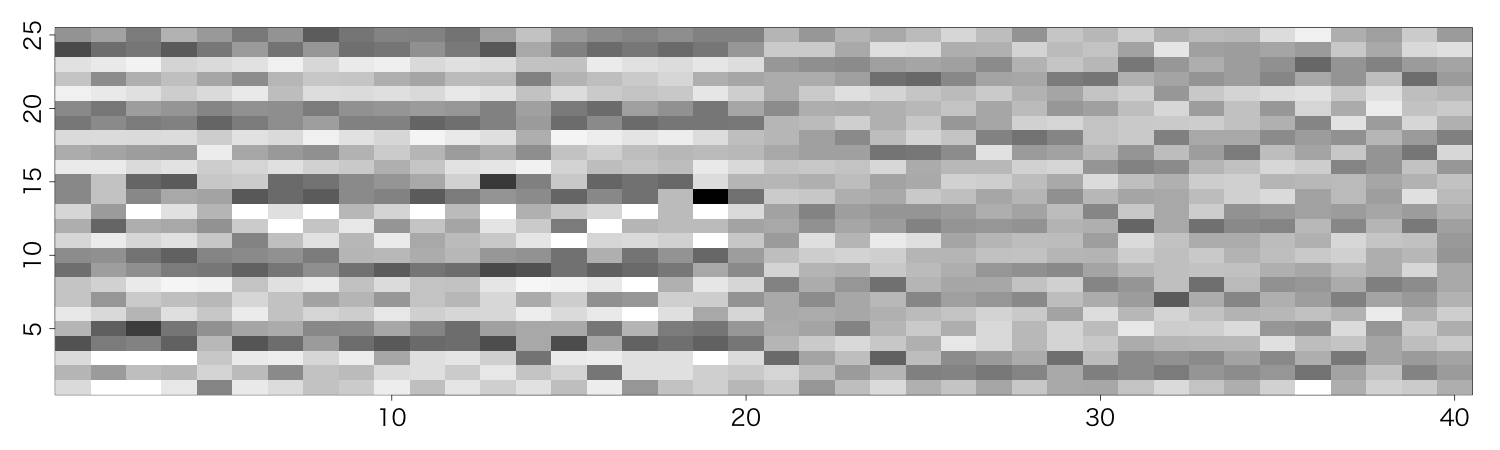
横軸はサンプル番号。
縦軸は、「A→A」「A→B」「A→C」..「E→E」という組み合わせ。25種類。
遷移確率=最小値だと白、=最大値だと黒。
この場合、
range(Result)
[1] 0.00 0.75
最初の20サンプルは"D"と"E"が多いので、それに対する遷移に偏っている。
後の20サンプルは、緩やかに"B"と"C"が多くなっているので、パタンが分かれている。
いや、まぁ、どうやっても書けるんですが。
200文字列の、「1~199番目」をdat1に、「2~200番目」をdat2に入れて、
table(dat1, dat2)
とすれば「遷移数」は出るかな、と考える。
ただし、「5種類」が全て出現するとは限らないので、factor(hoge, levels=c(1:5))としているのはそのため。
割り算は、まぁなんとなくapply。
もっと格好良く書けるはず。
Result <- NULL
for(i in 1:ncol(dat)){
dati <- factor(dat[,i], levels=c(1:5))
dat1 <- dati[1:(length(dati)-1)]
dat2 <- dati[2:length(dati)]
a <- function(a){a/table(dati)}
tpi <- apply(table(dat1, dat2), 2, a)
Result <- cbind(Result, c(t(tpi)))
}
3. Jensen-Shannon Divergence
元のデータだと「文字が何番目に現れるか」という情報を持つ。
サンプル1とサンプル2の「N番目」が同じ意味を持つかどうかがよく分からないため、比較していいのかよく分からない。
遷移確率マトリックスに直すと「A→Bの確率」というサンプルを超えて比較可能な情報に変換されているため、比較しやすい。
あとはこの確率のセットをどうやって比較するか、という事になる。
クラスタ化を遠目に見ているので、「対称」で「距離」として使える情報がいい。
エントロピーを規格化して対称になるように補正したJS divergenceを使おう。
これを求めるには、非対称なKullback-Leiber dicergenceを求めて、補正する。
KL divergenceはentropy::KL.pluginで求められる。
もう、for文でいいですよね?
library("entropy")
matJSD <- matrix(0, ncol(Result), ncol(Result))
for(i in 1:ncol(Result)){
for(k in 1:ncol(Result)){
a <- Result[,i]
b <- Result[,k]
JSD_ik <- try(sum(KL.plugin(b,(a+b)/2),
KL.plugin(a,(a+b)/2))/2, silent=F)
if(class(JSD_ik)!="try-error"){
matJSD[i, k] <- JSD_ik
}
}
}
警告は、確率0のlogを取ると計算不能になるのを回避するため。
っという事で、
白ければ白いほど、JSDが小さい。
4 clustering
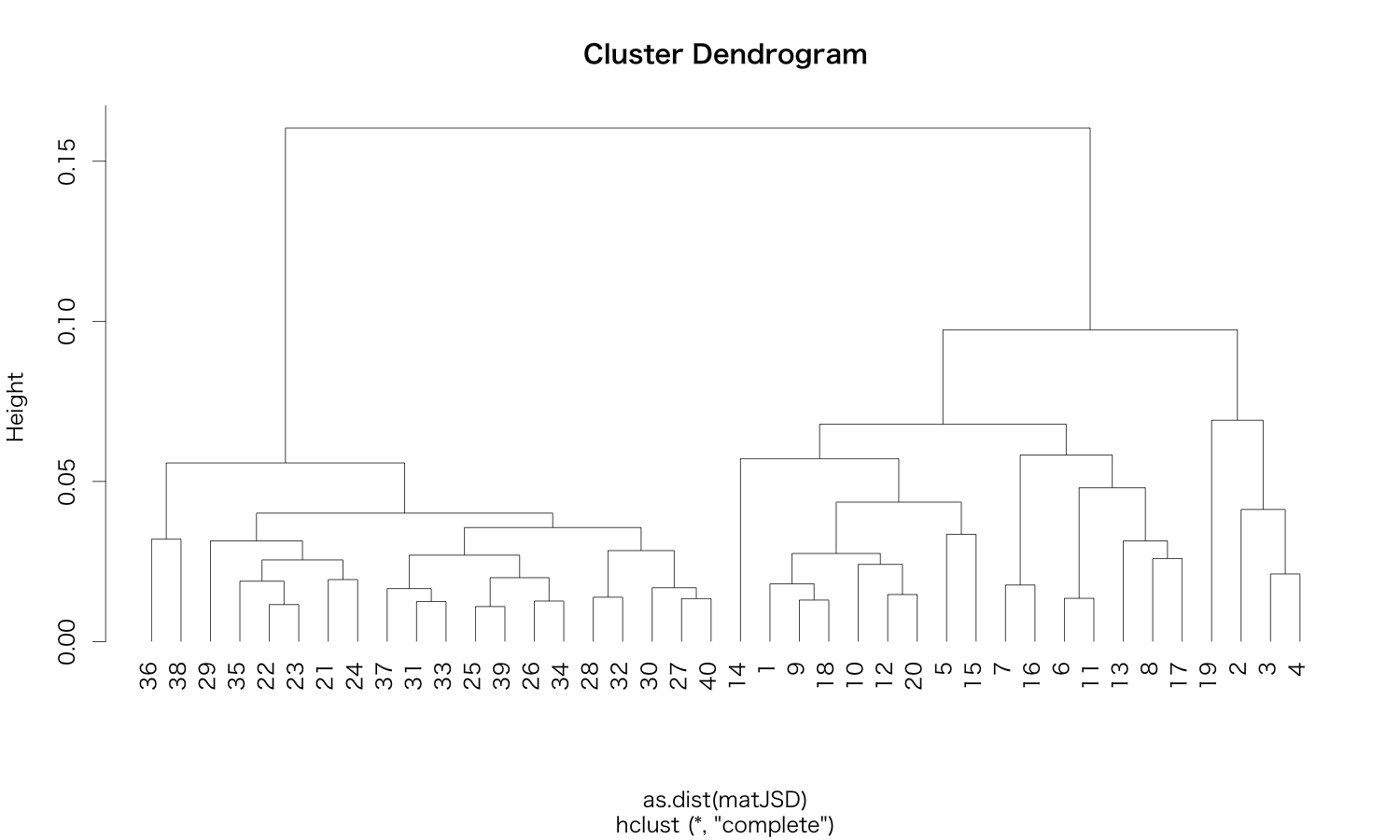
これはもう説明不要でしょう。
plot(hclust(as.dist(matJSD)), hang=-1)
っという事で、メデタシ。