統計をこれから学ぼうという方にとって、非常に重要な概念ですが理解が難しいものに「標準偏差」があると思います。「平均」くらいまでは馴染みもあるし、「わかるわかるー」という感じと思いますが、突如現れる「標準偏差」
\sigma = \sqrt{ {1 \over n} \sum_{i=1}^n(x_i - \bar{x})^2}
の壁。結構、この辺りで、「数学無理だー」って打ちのめされた方もいるのではないでしょうか。
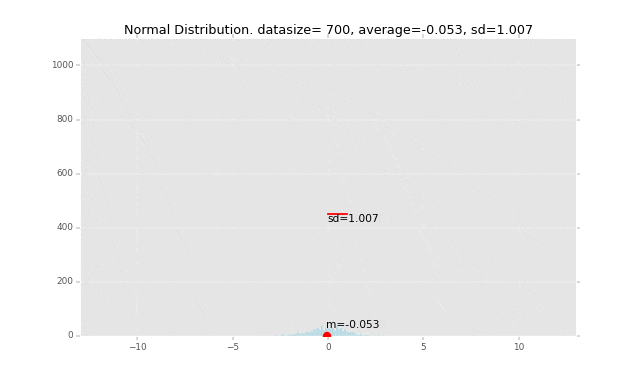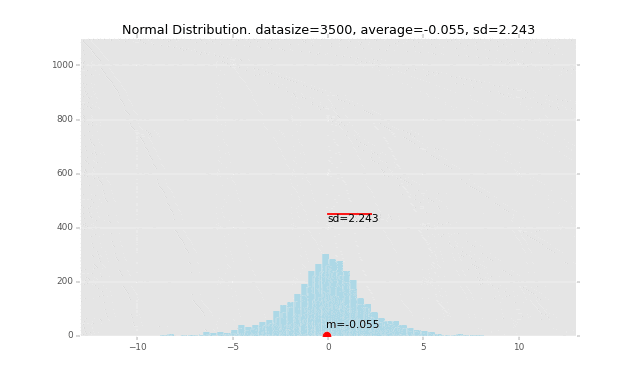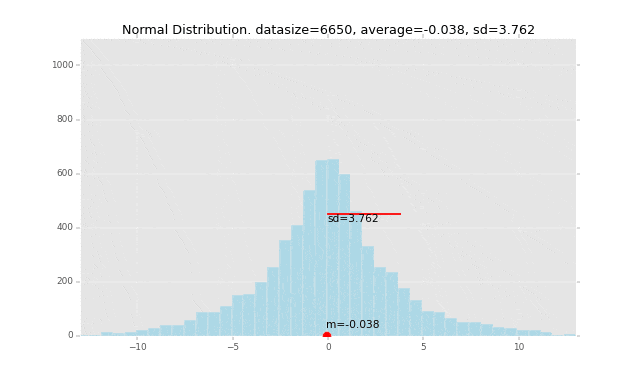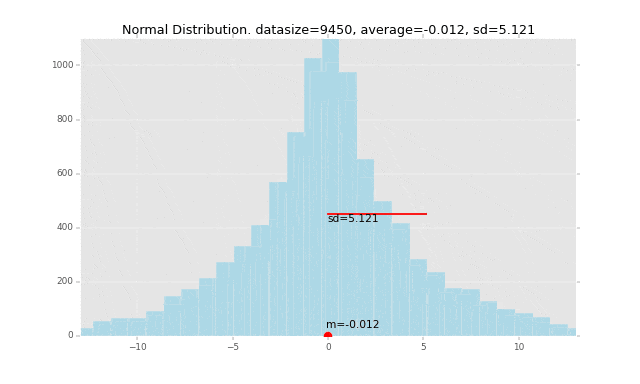
先にグラフのイメージを掲載すると、下記の赤い線の長さが「標準偏差」です。なぜこの長さが標準偏差なのか、ということも解き明かしていきます。
(code is here)
本記事では数学が得意でない方にもわかるように1から標準偏差とはなにか、を説明してみようという記事です。
数式はわかるけど、イマイチ「標準偏差」の意味わからんという方にも直感的な理解がしてもらえるような説明もしていきますので、ぜひご覧ください。
(※ この記事では標準偏差の分母に $n$を使用しています。$n-1$を使用するケースもあり、分析するケースにより使い分けますが、ここでは表記が少しでも簡単な方の $n$をつかって説明します。)
0.記号について
数学が馴染みがない方がつまずくのが、やっぱりまず数学の記号。
「$x_i$」ってなんやねん、とか
\sum_{i=1}^n x_i
なんてさっぱりという方への説明です。
この辺りの数学記号がOKな方は次の節へジャンプしてください。
まず$x_i$から紐解いていきます。
みなさんExcel使いますよね。まず、こんなテストのデータがあったとします。
| 名前 | 数学 |
|---|---|
| 田中 |
96 |
| 高橋 |
63 |
| 鈴木 |
85 |
| 渡辺 |
66 |
| 清水 |
91 |
| 木村 |
89 |
| 山本 |
77 |
合計すると、
合計点数 = 田中(数学) + 高橋(数学) + 鈴木(数学) + 渡辺(数学) + 清水(数学) + 木村(数学) + 山本(数学)
\\
= 96 + 63 + 85 + 66 + 91 + 89 + 77 = 567
と計算できます。
名前ではなくIDが使われているとすると、
| ID | 数学 |
|---|---|
| 1 | 96 |
| 2 | 63 |
| 3 | 85 |
| 4 | 66 |
| 5 | 91 |
| 6 | 89 |
| 7 | 77 |
合計点数 = {\rm ID}:1(数学) + {\rm ID}:2(数学) + {\rm ID}:3(数学) + {\rm ID}:4(数学) + {\rm ID}:5(数学) + {\rm ID}:6(数学) + {\rm ID}:7(数学)
\\
= 96 + 63 + 85 + 66 + 91 + 89 + 77 = 567
です。点数を数字ではなく変数に置き換えてみます。ID:1の人の点数は$x_1$になります。右下の数字がIDを表しています。すると先ほどの点数の合計の式は
合計点数 = {\rm ID}:1(数学) + {\rm ID}:2(数学) + {\rm ID}:3(数学) + {\rm ID}:4(数学) + {\rm ID}:5(数学) + {\rm ID}:6(数学) + {\rm ID}:7(数学)
\\
= x_1 + x_2 + x_3 + x_4 + x_5 + x_6 + x_7
\\
= 96 + 63 + 85 + 66 + 91 + 89 + 77 = 567
と表されます。ここまではデータが7個だったので地道に上記のように足し算を並べればよかったのですが、データが1000個あったときは、とてもじゃないけど書ききれないですね。
そこで便利なのが先ほどの $\sum$なのです!
点数の合計 = {\rm ID}:1(数学) + {\rm ID}:2(数学) + {\rm ID}:3(数学) + {\rm ID}:4(数学) + {\rm ID}:5(数学) + {\rm ID}:6(数学) + {\rm ID}:7(数学)
\\
= x_1 + x_2 + x_3 + x_4 + x_5 + x_6 + x_7
\\
= \sum_{i=1}^7 x_i
\\
= 96 + 63 + 85 + 66 + 91 + 89 + 77 = 567
のように表されます。つまり、

ということで
\sum_{i=1}^7 x_i = x_1 + x_2 + x_3 + x_4 + x_5 + x_6 + x_7
になります。こうするとデータが1000個あった時も
\sum_{i=1}^{1000} x_i = x_1 + x_2 + \cdots + x_{1000}
と表すことができて便利なので使われているのです。
そもそも、個数が事前に決まっていれば、気合で1000個書き並べることも不可能ではないのですが、データの個数が現時点で分かっておらず、とりあえず$n$個、と仮置きした時も、
\sum_{i=1}^{n} x_i
と、決まっていない場合でも書けてしまうのです!便利!
ちなみにコードで表した方がわかる方は、下記の処理であると言った方がすぐわかるかもしれません。$\sum$記号というものは、for文で回して足し合わせるという処理のことですね。
x = [96, 63, 85, 66, 91, 89, 77]
total = 0
for i in range(len(x)):
total += x[i]
print total
1.何はともあれ、まずは平均
改めて「平均」を考えてみましょう。平均も種類があって「算術平均」・「幾何平均」・「調和平均」とかあるのですが、いわゆる馴染みのある「平均」は「算術平均」です。
データを全て足し合わせて、その数で割ったものですね。統計学ではこの「平均」を $\bar{x}$と表し、定義は下記です。データの数は $n$とします。前項の数学のテストの例だと、7人の生徒のデータなので $n=7$になります。
\bar{x} = {1 \over n} \sum_{i=1}^{n} x_i
(もし記号の意味がよく分からない場合は、前項を確認してみてください)
グラフで表すと下記のようになります。これは直感通りですね ![]()
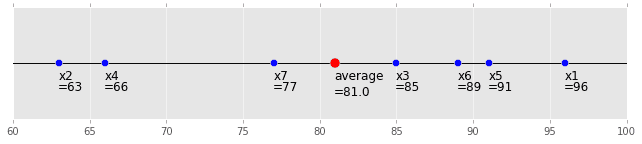
(code is here)
2.「偏差」とは?
さて次に、「偏差」という概念の説明です。「標準偏差」と、あるように少し核心に近づきます。
偏差とは下記のように、各データと平均の差のことです。
| ID | 点数 | 偏差 |
|---|---|---|
| 1 | 96 | 96-81= 15 |
| 2 | 63 | 63-81= -18 |
| 3 | 85 | 85-81= 4 |
| 4 | 66 | 66-81= -15 |
| 5 | 91 | 91-81= 10 |
| 6 | 89 | 89-81= 8 |
| 7 | 77 | 77-81= -4 |
これもグラフで表してみます。赤い線の部分が各データの偏差です。
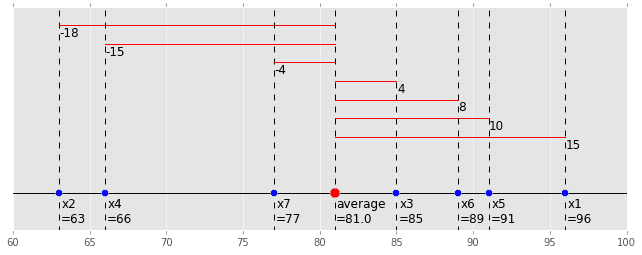
(code is here)
3.平均偏差
さて、標準偏差に移る前に、直感的な理解がしやすい「平均偏差」を紹介します。
前項で説明した「偏差」の平均です。つまり
| ID | 偏差 |
|---|---|
| 1 | 15 |
| 2 | -18 |
| 3 | 4 |
| 4 | -15 |
| 5 | 10 |
| 6 | 8 |
| 7 | -4 |
の平均を考えるのですが、ただ1つ問題がありまして、これ、全部足すと0になっちゃうのです。
やりたいのは

の赤い線の長さの平均なので、マイナスを抜いてしまいます。
| ID | 偏差の絶対値 |
|---|---|
| 1 | 15 |
| 2 | 18 |
| 3 | 4 |
| 4 | 15 |
| 5 | 10 |
| 6 | 8 |
| 7 | 4 |
この「偏差の絶対値」の平均値をとると 10.57 になり、この値が「平均偏差」と呼ばれます。
これは、
- 平均値からの距離の平均
- 平均からどのくらい離れているかの指標
と、考えられます。
今回の例で言うと、平均点81点に対し、平均して10.57点くらい離れている、ということになります。
この概念がほとんど標準偏差の考えといっても過言ではありません。計算のアプローチが少し違うだけです。
なので、「標準偏差」と言ったらこの「平均からどのくらい離れているかの平均」というイメージをしてもらえればと思います。
数式を使ってこれを表現します。
まず、絶対値の記号ですが、$|x|$のように表現し、マイナスの数字は$|-4| = 4$のようにマイナスが除去され、プラスの数字は$|4|=4$のように変化しません。
グラフで書くとこのように表され、$x$がマイナスの領域で値がプラスになるように傾きが反転しています。
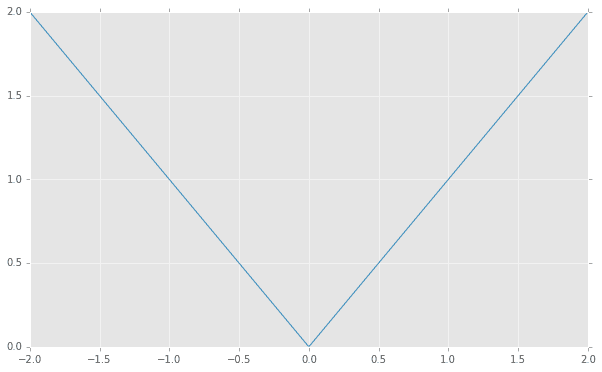
(code is here)
数式で表すとこうなります。

データの値から平均を引いて偏差を作り、絶対値をとることでマイナスを除去して、それの平均を取っている、と解釈できます。
Pythonコードで表すとこのようになります。
x = [96, 63, 85, 66, 91, 89, 77]
ave = np.average(x)
total = 0
for i in range(len(x)):
total += abs(x[i] - ave)
print total/len(x)
4.標準偏差
さて、最後に本記事の主役、「標準偏差」です。
「平均偏差」では、絶対値を使ってマイナスをプラスに変える操作をしましたが、「標準偏差」では二乗してマイナスを取る、という方式に変えたものです。
つまり、考え方は全く同じで、マイナスの除去方法が違うだけです。
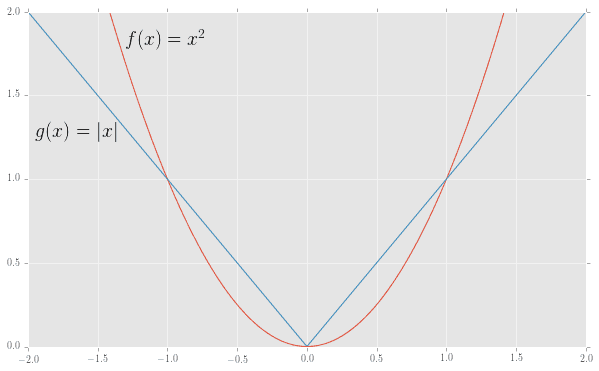
下記のように、原点を折り返しポイントとして左右対称で、マイナスの値をプラスに変えているという類似点がありますね。
(code is here)
(青い線が絶対値関数$g(x)=|x|$、赤い線が二乗の関数で$f(x)=x^2$です)
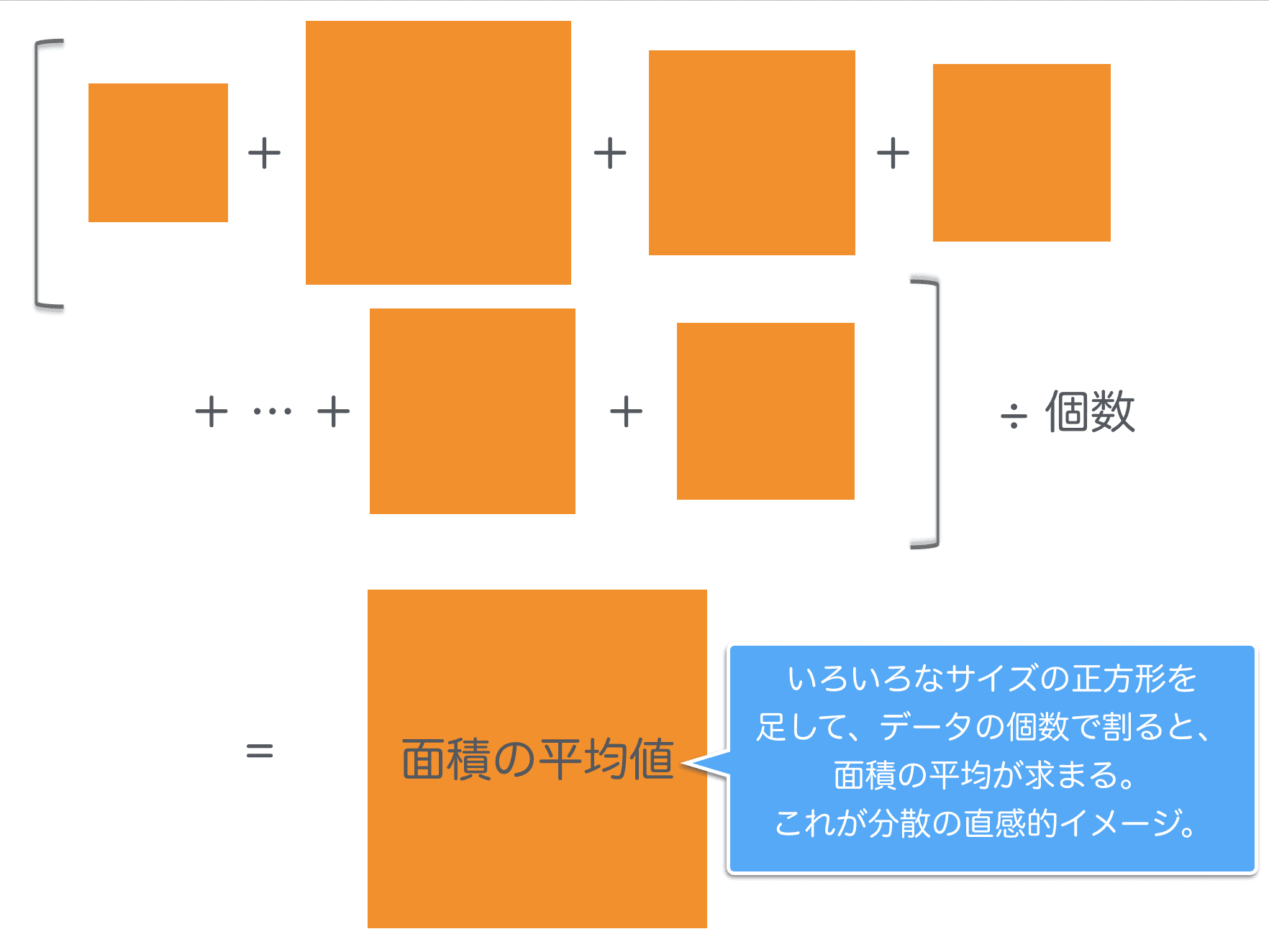
前項では下記の図のように、平均値からの差を線の長さで表現していましたが、
今度はこちらのように正方形の面積で、平均値からの離れ具合を評価するのが、二乗で差を評価するイメージです。
これを数式で表すと、

この、平均からの偏差を二乗したものを足し合わせて平均を取ったものを「分散」と言います。
ここまでくると、「標準偏差」あと一歩です。
本記事の冒頭で示した式を再掲すると下記になります。
\sigma = \sqrt{ {1 \over n} \sum_{i=1}^n(x_i - \bar{x})^2}
「分散」との違いはルートの計算をするかどうか、の違いです。
「分散」でもデータの散らばりの具合の指標にはなりますが、面積で考えてしまっているので単位が変わってしまっています。そこでルート$\sqrt{\ \ }$をとることで、面積を長さに戻すことができます。
ルート$\sqrt{\ \ }$は二乗したらその値になるもの、という定義で、$\sqrt{9} = \sqrt{3^2} = 3$とか、$\sqrt{25} = \sqrt{5^2} = 5$の関係を表します。 $3^2 = 9$の逆の計算ですね。$25$ は $5\times5$の正方形の面積と考えることができるので、

数式で書くとこうなります。分散全体に対してルート$\sqrt{\ \ }$の計算をします。上記の面積の平均値に対して、「辺の長さを取り出す操作」と考えられますね。
つまり、標準偏差は
標準偏差 = \sqrt{分散}
となるのです。
Pythonコードで表すとこのようになります。
x = [96, 63, 85, 66, 91, 89, 77]
ave = np.average(x)
total = 0
for i in range(len(x)):
total += (x[i] - ave)**2
print np.sqrt(total/len(x))
また、なぜ「絶対値」ではなく「二乗」に変えたのか、の理由は少し難しいのですが、平均偏差に使われる絶対値の処理が、数学的に扱いが難しいため、扱いやすい二乗を採用した、という点がひとつ。あとは、距離の概念としては二乗してルートをとることが三平方の定理からわりと自然であることも理由の一つと考えています。
まとめると
- 数学的な取り扱いが便利になる
- そもそも距離の概念が、二乗してルートをとるとして定義できるため
と考えます。(もう少し詳細な説明はそのうち別記事で考えます ![]() )
)
5.例1:グラフで理解
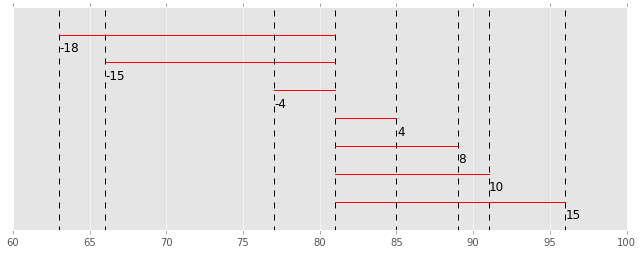
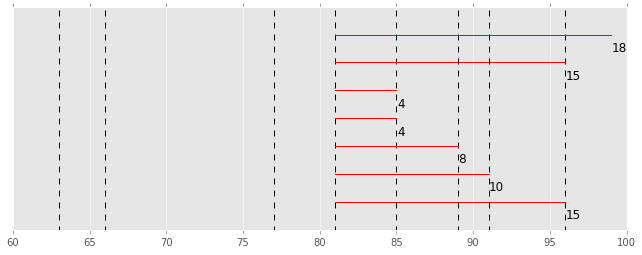
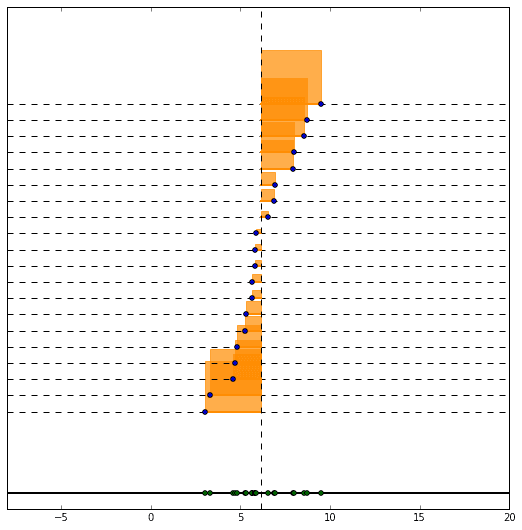
冒頭にも掲載しましたが、例を一つグラフで書いてみます。
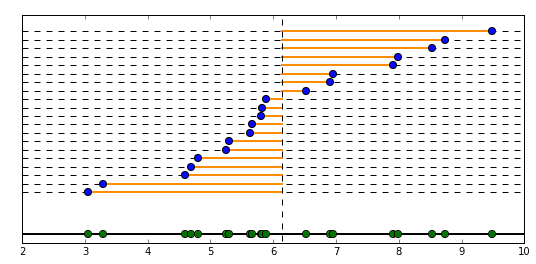
このデータの平均を赤い丸で表し、1つ1つのデータの平均からの偏差を計算して、そこからさらに標準偏差を計算して赤い棒の長さで表現しています。
全データの平均値からの距離の平均がこの赤い棒の長さになるイメージです。
段々広範囲にデータが発生するように作っているので、標準偏差の棒の長さも長くなっていきます。

(code is here)
6.例2:偏差値
大学受験等でおなじみ偏差値ですが、この偏差値も「標準偏差」を元に作られています。
テストを受けた全員のデータから平均、標準偏差を計算して求めます。そして、
- 平均点の人が偏差値50
- 平均より標準偏差1つ高い点数を取った人を偏差値60
- 平均より標準偏差1つ低い点数を取った人を偏差値40
のように計算します。つまり、
偏差値 = { (点数 - 平均) \over 標準偏差} \times 10 + 50
のように計算された値なのです。
前項のグラフの赤い棒の長さ分だけ平均より点数が高いと、偏差値60ということですね!
#最後に
いかがでしたでしょうか?自分の中で可能な限り丁寧に説明してみましたが、改めて整理してみると結構多彩な要素が絡み合って構成されている概念であることが自分でも再認識できました。ですが、一つ一つの要素をきちんと理解できれば、全体の直感も持つことができるではと考えています。
この標準偏差の理解で「統計学面白い!」と思ってもらい、データ分析に興味を持つ人が増えてくれたら幸いです!
(※もし、「イマイチわからん」という部分がありましたらコメント欄にてお願いします!)
また、「統計学の基礎の基礎」という記事(スライド)も書きましたので、よければこちらも関連記事としてご参照ください。
http://qiita.com/kenmatsu4/items/5a59a7375140f29b31c2