LoginSignup
64
70

More than 5 years have passed since last update.

@kenmatsu4(まつ けん)

【機械学習】「異常検知と変化検知」 Chapter 1の図をPythonで描いてみる。

Last updated at Posted at 2015-08-22

ウワサの赤い本、機械学習プロフェッショナルシリーズ「異常検知と変化検知」(http://ide-research.net/book/support.html#kodansha) 第1章のグラフをPythonで書いてみる、という記事です。

こんな感じで、アニメーションで標本精度とROC曲線を描いたりしています。

ROC_curve2.gif

コードの全体はこちら

解説は簡易的なものしかここでは記載していませんので、詳細を知りたい方は是非本をご購入ください！

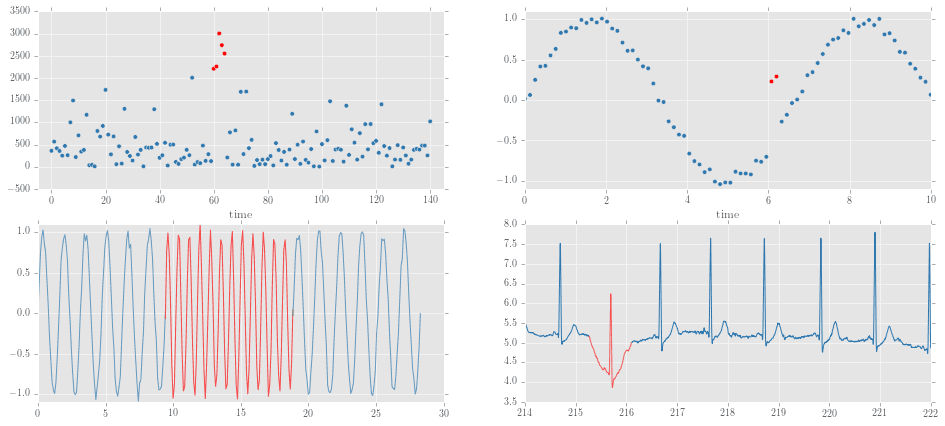
図1.1 時系列データの様々な異常の例

全く同じデータではなく、似たようなデータをPythonで生成、もしくはデータを探してplotしました。
（特に心電図データ1は探すのが一苦労でした・・・ :sweat_smile: ）

anomaly_detection_1.1-compressor.png
これを描画するコード全体はこちら

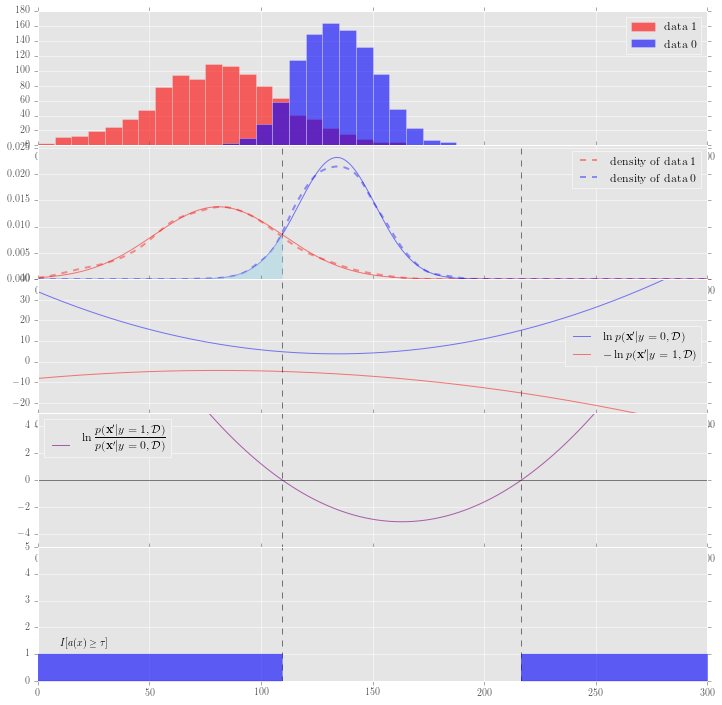
図1.2 ラベル付きデータについての異常判定の説明

図1.2から異常度、指示関数をつなげて描画して関連性を可視化してみました。

  1. ２つの正規分布に従う乱数からデータ生成し、青を正常データ、赤を異常データとしてplot
  2. 1.のヒストグラムから平均、標準偏差を算出し、正規分布の密度関数を描画。（分布からカーネル密度推定したものも点線で描画）
  3. $\ln p({\bf x}'|y=0,\mathcal{D})$、$-\ln p({\bf x}'|y=1,\mathcal{D})$を別々に描画。
  4. 異常度$a(x') \ln{ p({\bf x}'|y=1,\mathcal{D})\over p({\bf x}'|y=0,\mathcal{D})} $を描画
  5. 指示関数 $I[a(x) \ge \tau]$ を描画

さらに、分岐点閾値を密度関数の値が同じになる点として計算し、その場合の$\tau$を4つ目のグラフの横棒で表しています。

anomaly_detection_1.2.png
これを描画するコード全体はこちら

Pythonコード

# 乱数生成
rd.seed()
n = 1000
d_0 = rd.normal(135, 18, n)  # 正常データ
d_1 = rd.normal(80, 30, n)   # 異常データ

# 平均、標準偏差の算出
m_0  = np.mean(d_0)
sd_0 = np.sqrt(np.var(d_0))
m_1  = np.mean(d_1)
sd_1 = np.sqrt(np.var(d_1))

# X軸データ生成
xx = np.linspace(0,300, 5000)

# 正規分布の密度関数
density_0 = st.norm.pdf(xx, m_0, sd_0)
density_1 = st.norm.pdf(xx, m_1, sd_1)

# 異常度の計算
abnormaly_score = np.log(density_1) - np.log(density_0)

def balance_position(x_min, x_max, f1, f2, EPS=0.00001):
    if abs(f1(x_max) - f2(x_max)) > EPS:
        center = (x_min + x_max)/2.
        if np.sign(f1(x_max) - f2(x_max)) * np.sign(f1(center) - f2(center)) < 0:
            x_min = center
        else:
            x_max = center
        x_max = balance_position(x_min, x_max, f1, f2)
    else:
        return x_max
    return x_max

mark = balance_position(0, 200, lambda x:st.norm.pdf(x, m_0, sd_0), lambda x: st.norm.pdf(x, m_1, sd_1)) 
print "mark:", mark

tau_pos = np.argsort(np.abs(xx - mark))[0]
print "tau pos:", tau_pos

tau = abnormaly_score[tau_pos]
print "tau:", tau

tau2_pos = np.max(np.argsort(np.abs(abnormaly_score - tau))[0:2])
print "tau2_pos:",tau2_pos

tau2 = abnormaly_score[tau2_pos]
print "tau2:",tau2

mark2 = xx[tau2_pos]
print "mark2:",mark2

#---------------- 描画処理 -----------------#
n_row = 5                         # グラフの行数

plt.subplots(n_row, 1, sharex=True,figsize=(12,12)) 
gs = gridspec.GridSpec(n_row, 1, height_ratios=[3,3,3,3,3])

axs = [plt.subplot(gs[i]) for i in range(n_row) ]
# 1つ目のエリア描画
axs[0].hist(d_1, bins=40, color="r", alpha=0.6, range=(0,300), label="data 1")
axs[0].hist(d_0, bins=40, color="b", alpha=0.6, range=(0,300), label="data 0")
axs[0].legend(loc='best')

# 2つ目のエリア描画
axs[1].plot(xx, get_density(d_1, xx), "r--", alpha=.4 , lw=2, label=r"density of data 1")
axs[1].plot(xx, get_density(d_0, xx), "b--", alpha=.4 , lw=2, label=r"density of data 0")
axs[1].legend(loc='best')
axs[1].plot([0,300],[0,0],"k")
axs[1].plot(xx, density_1, c="r", alpha=.5 )
axs[1].plot(xx, density_0, c="b", alpha=.5 )
axs[1].fill_between(xx[0:tau_pos], density_0[0:tau_pos], color="lightblue", zorder = 500, alpha=.6)
axs[1].set_ylim(0,np.max(density_0)*1.1)
axs[1].plot([mark ,mark],[-100,200], "k--", lw=.5)
axs[1].plot([mark2 ,mark2],[-100,200], "k--", lw=.5)

# 3つ目のエリア描画
axs[2].plot(xx, -np.log(density_0), c="b", alpha=.5,  label=r"$\ln p({\bf x}'|y=0,\mathcal{D})$")
axs[2].plot(xx,  np.log(density_1), c="r", alpha=.5, label=r"$-\ln p({\bf x}'|y=1,\mathcal{D})$")
axs[2].plot([mark ,mark],[-110,200], "k--", lw=.5)
axs[2].plot([mark2 ,mark2],[-110,200], "k--", lw=.5)
axs[2].set_ylim(-25,40)
axs[2].legend(loc='best')

# 4つ目のエリア描画
axs[3].plot(xx, abnormaly_score, c="purple", alpha=.6, label=r"$$ \ln{ p({\bf x}'|y=1,\mathcal{D})\over  p({\bf x}'|y=0,\mathcal{D})} $$")
axs[3].set_ylim(-5,5)
axs[3].plot([mark ,mark],[-100,200], "k--", lw=.5)
axs[3].plot([mark2 ,mark2],[-100,200], "k--", lw=.5)
axs[3].plot([0 ,300],[tau, tau], "k", lw=.5)
axs[3].legend(loc='best')

# 5つ目のエリア描画
axs[4].fill_between(xx[0:tau_pos], np.ones_like(xx[0:tau_pos]), color="blue", zorder = 500, alpha=.6)
axs[4].fill_between(xx[tau2_pos:], np.ones_like(xx[tau2_pos:]), color="blue", zorder = 500, alpha=.6)
axs[4].plot([mark, mark],[-110,200], "k--", lw=.5)
axs[4].plot([mark2, mark2],[-110,200], "k--", lw=.5)
axs[4].text(10, 1.3, r"$I[a(x) \ge \tau]$")
axs[4].set_ylim(0,5)

# すべてのエリアでxの範囲を固定
for ax in axs:
    ax.set_xlim(0,300)

plt.subplots_adjust(hspace=0)

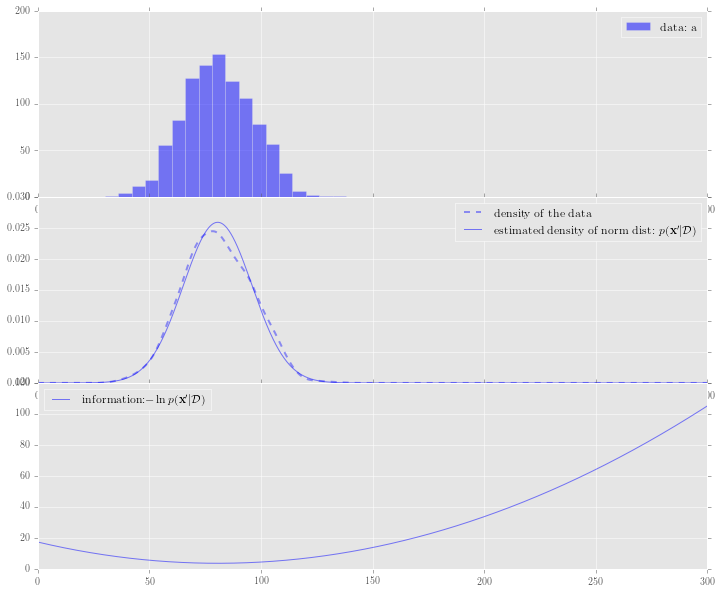
図1.3 ラベルなしデータについての異常度の定義

図1.2と同様、ヒストグラム、カーネル密度、平均・分散から推定した正規分布の密度関数を描き、「情報量」のプロットをしています。異常度は単純にデータの平均から離れるほど高くなる形となっています。

anomaly_detection_002.png
これを描画するコード全体はこちら

Pythonコード

# ラベルなしデータの場合
# 乱数生成
n = 1000
data = rd.normal(80, 15, n)

# 平均、標準偏差の算出
m  = np.mean(data)
sd = np.sqrt(np.var(data))

# X軸データ生成
xx = np.linspace(0,300, 5000)

# 正規分布の密度関数
density = st.norm.pdf(xx, m, sd)

#---------------- 描画処理 -----------------#
n_row = 3                         # グラフの行数
xx = np.linspace(0,300, 5000)     # X軸データ生成

plt.subplots(n_row, 1, sharex=True,figsize=(12,10)) 
gs = gridspec.GridSpec(n_row, 1, height_ratios=[3,3,3])

axs = [plt.subplot(gs[i]) for i in range(n_row) ]

# 1つ目のエリア描画
axs[0].hist(data, bins=50, range=(0,300), label="data: a", color="b", alpha=0.5)
axs[0].set_ylim(0,200)
axs[0].legend(loc='best')

# 2つ目のエリア描画
axs[1].plot(xx, get_density(data, xx), lw=2, linestyle="--", label="density of the data", color="b", alpha=0.4)
axs[1].plot(xx, density, lw=1, label=r"estimated density of norm dist: $p({\bf x}'|\mathcal{D})$", color="b", alpha=0.5)
axs[1].legend(loc='best')

# 3つ目のエリア描画
axs[2].plot(xx, -np.log(density), lw=1, label=r"information:$-\ln p({\bf x}'|\mathcal{D})$", color="b", alpha=0.5)
axs[2].legend(loc='best')


# すべてのエリアでxの範囲を固定
for ax in axs:
    ax.set_xlim(0,300)

plt.subplots_adjust( hspace=0)

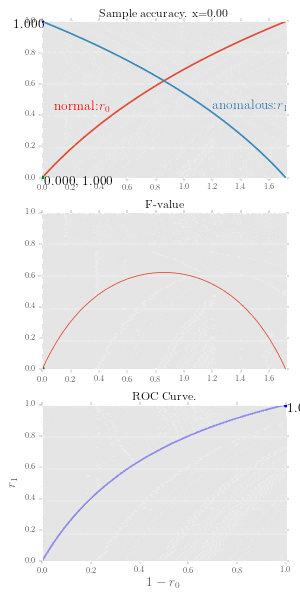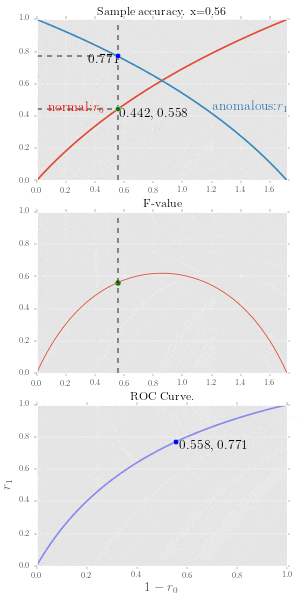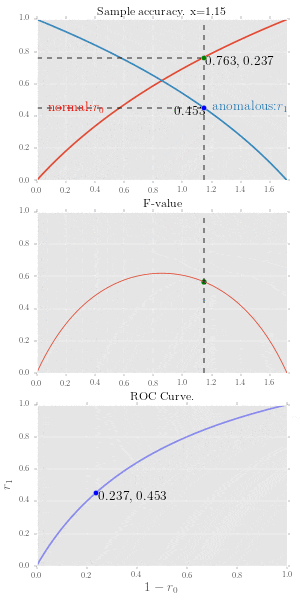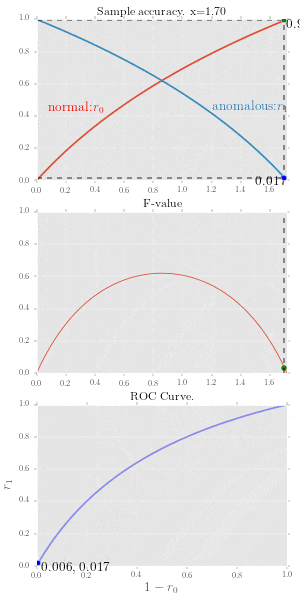
図1.4, 図1.5 正常標本精度、異常標本精度とROC曲線

正常標本精度、異常標本精度とROC曲線の関係をアニメーションにしてみました。
また、ROC曲線の詳細については以前に「統計学】ROC曲線とは何か、アニメーションで理解する。
」という記事も書いていますのでよければご参考ください。

この図では標本精度が下記で表せていたとして描いています。

r_0 = \log(1 + x) \\
r_1 = \log(e -x)

2段目のグラフはF値を表現しており定義は下記です。

f  \equiv　{ 2r_0 r_1 \over r_0 + r_1 }

ROC曲線は $(X, Y) = (1 - r_0(\tau),\ r_1(\tau))$なので、赤い線をなぞる点のy座標値は$1-y$を使います。座標をアニメーション上に表示していますが、二つあるうちの右側の数字がこれにあたります。

ROC_curve2.gif
これを描画するコード全体はこちら

Pythonコード

def animate(nframe):
    global num_frame
    sys.stdout.write(str(int(float(nframe)/num_frame*100)) + "%, ") 

    plt.clf()

    # xの最小値、最大値
    xmin = 0
    xmax = np.e -1

    # xの分割数
    sx = num_frame * 2

    # 現在位置
    pos = nframe * 2

    # x軸生成
    xx = np.linspace(xmin, xmax, sx)

    # 標本精度
    cx1 = np.log(1+xx)
    cx2 = np.log(np.e -xx)

    # 1つ目のグラフ描画 -----------------------
    plt.subplot(311)
    plt.title("Sample accuracy. x={0:.2f}".format(xx[pos]))
    plt.xlim(xmin, xmax)
    plt.ylim(0,1)

    # 曲線の描画
    plt.plot(xx,cx1,linewidth=2)
    plt.plot(xx,cx2,linewidth=2)

    # 点と座標値の描画
    plt.scatter(xx[pos],cx1[pos], c="g", s=40, zorder=100)
    plt.text(xx[pos]+.01,cx1[pos]-.05,"{0:.3f}, {1:.3f}".format(cx1[pos], 1-cx1[pos]), size=16)
    plt.scatter(xx[pos],cx2[pos], c="b", s=40, zorder=100)
    plt.text(xx[pos]-.20,cx2[pos]-.05,"{0:.3f}".format(cx2[pos]), size=16)

    # 点線の描画
    plt.plot([xx[pos], xx[pos]], [0,1], "k--", alpha=.5, lw=2 )
    plt.plot([0, xx[pos]], [cx1[pos],cx1[pos]], "k--", alpha=.5, lw=2 )
    plt.plot([0, xx[pos]], [cx2[pos],cx2[pos]], "k--", alpha=.5, lw=2 )

    plt.text(.08, .42, r"normal:$r_0$", color="r", size=16)
    plt.text(1.2, .42, r"anomalous:$r_1$", color="#2F79B0", size=16)

    # 2つ目のグラフ描画 -----------------------
    plt.subplot(312)
    plt.title("F-value")
    plt.xlim(xmin, xmax)
    plt.ylim(0,1)
    F = 2*cx1*cx2/(cx1+cx2)
    F_pos = 2*cx1[pos]*cx2[pos]/(cx1[pos]+cx2[pos])
    plt.scatter(xx[pos], F_pos, c="g", alpha=1, s=50)
    plt.plot(xx, F)
    plt.plot([xx[pos], xx[pos]], [0,1], "k--", alpha=.5, lw=2 )
    plt.tight_layout()

    # 3つ目のグラフ描画 -----------------------
    plt.subplot(313)

    plt.title("ROC Curve.")
    plt.xlim(0,1)
    plt.ylim(0,1)

    # 曲線と点の描画
    plt.plot(1-cx1, cx2, linewidth=2, color="b", alpha=.4)
    plt.scatter(1-cx1[pos],cx2[pos], c="b", s=40, zorder=100)
    plt.text(1-cx1[pos]+.01,cx2[pos]-.05, "{0:.3f}, {1:.3f}".format(1-cx1[pos], cx2[pos]), size=16)

    plt.xlabel(r"$1-r_0$", size=16)
    plt.ylabel(r"$r_1$", size=16)
    plt.tight_layout()

num_frame = 50
fig = plt.figure(figsize=(5,10))
anim = ani.FuncAnimation(fig, animate, frames=num_frame, blit=True)
anim.save('ROC_curve2.gif', writer='imagemagick', fps=3, dpi=60)

参考図書

「異常検知と変化検知」　井手剛、杉山将著　（機械学習プロフェッショナルシリーズ）
　　http://ide-research.net/book/support.html

  1. 異常にした赤い部分は加工したものなので、正しい心電図データではないことにご注意ください。データの取得先URLについては、GitHubの方に記載してあります。 ↩

64
70
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
64
70