統計学、パターン認識等で、ROC(Receiver Operating Characteristic;受信者動作特性)曲線という概念が出てきます。また、データ分析・予測のコンペティションサイトKaggleでも、提出されたアルゴリズムの識別性能評価にこのROC曲線に基づくAUC(Area Under the Curve)というものを使っています。(例えばココ)
このROC曲線、ちょっとわかりにくいので、まとめてみました。また、アニメーションでグラフを動かしてイメージを付けるということもやってみます。
1. ROC曲線に至る前説
まず、例として健康に関するとある検査数値データがあったとします。
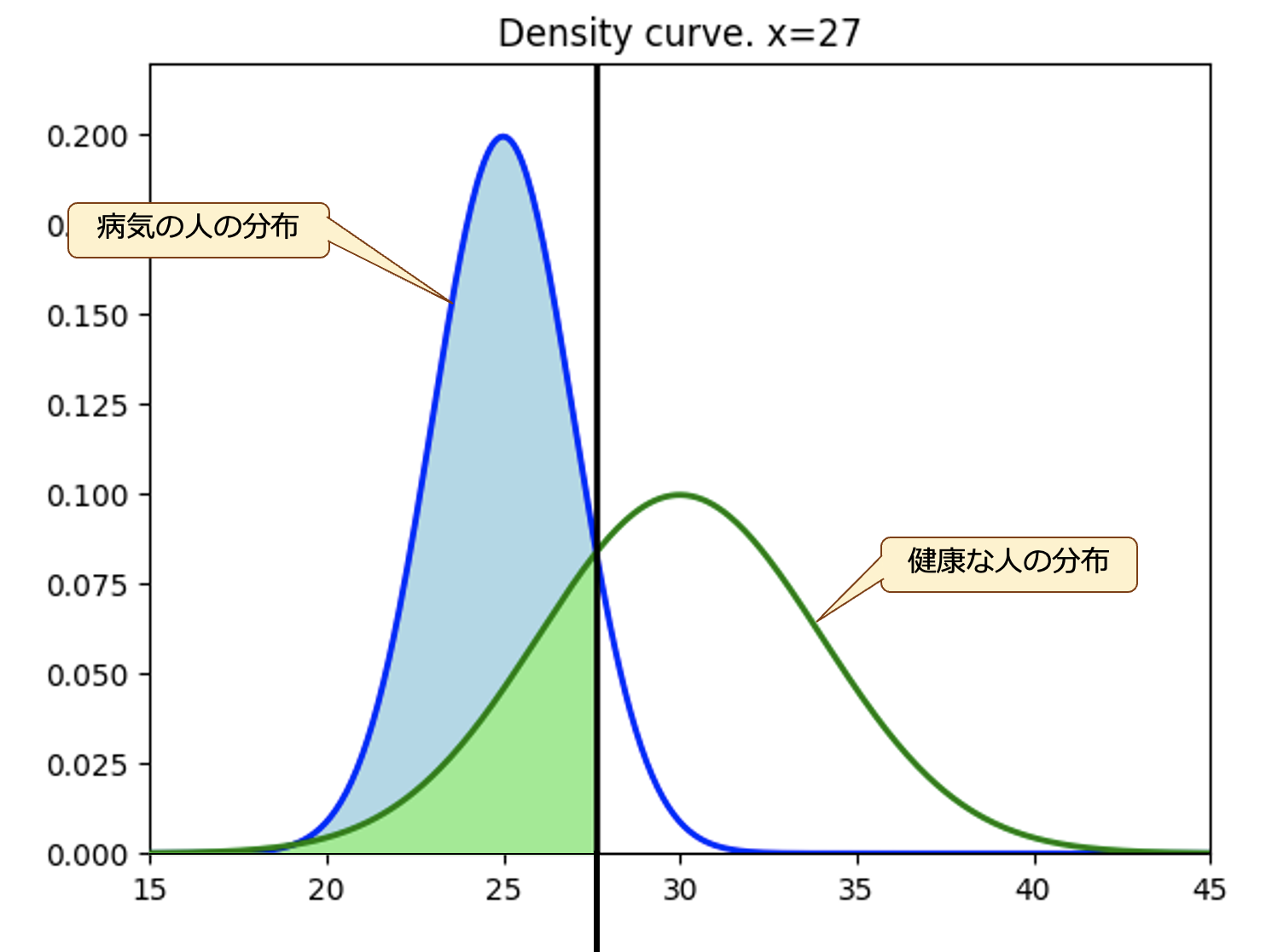
この検査数値は健康な人は平均25, 標準偏差2の正規分布に従い分布しています。(下記図の緑の曲線)
病気の人は平均30、標準偏差4の正規分布に従い分布しています。(下記の図の青の曲線)
グラフにすると下記のような関係になります。
このようなデータを持っているときに、この検査数値でその人が健康なのか、病気なのかを識別したい、というような問題を考えます。
例えば、「この検査数値が27未満の場合は病気、27以上の場合は健康」、と判断するという基準を設定するとします。
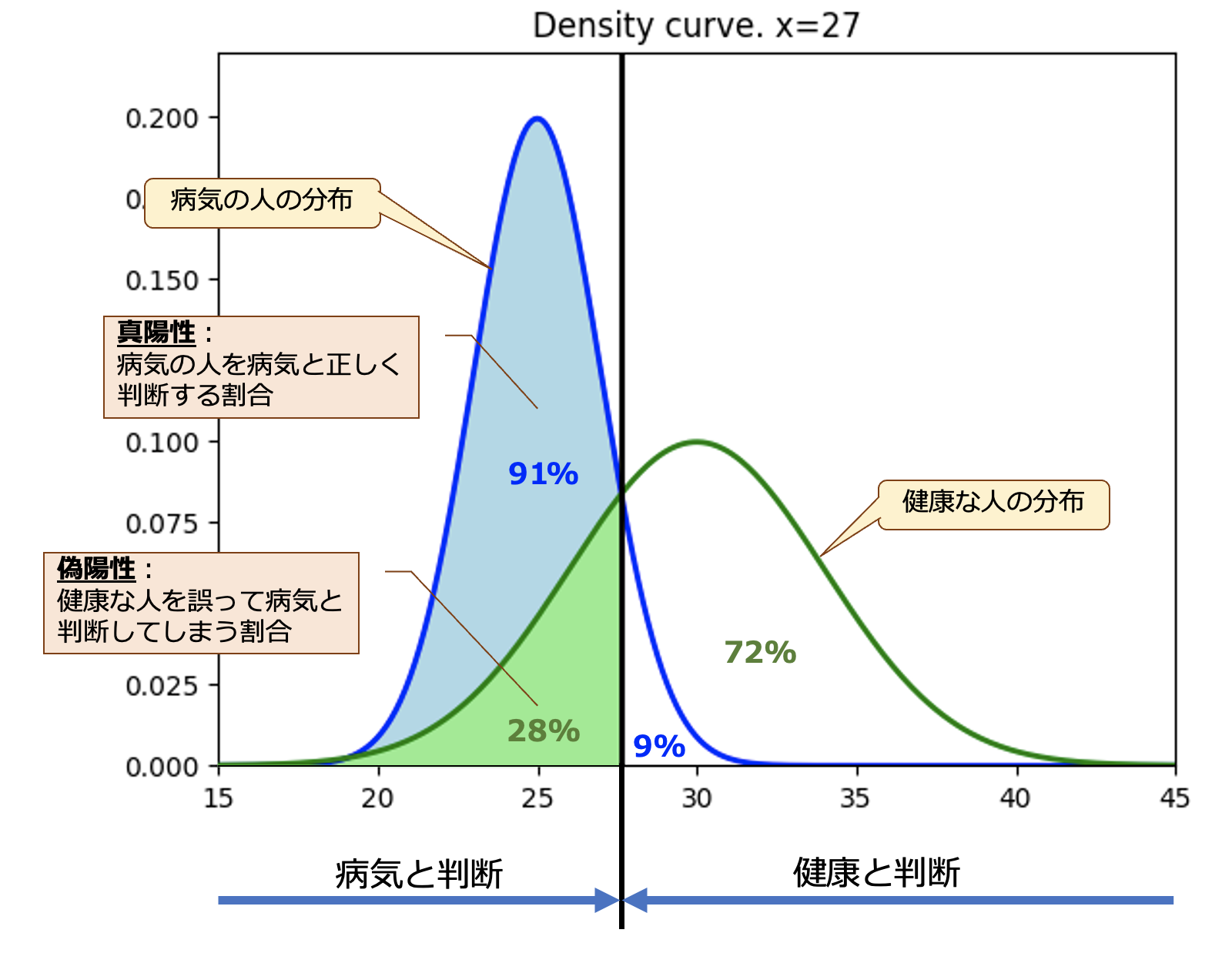
その時、上記のグラフに照らし合わせると青い線で表される面積と水色で塗りつぶされた面積の割合つまり、数値が27となっている部分の黒い縦線より左の面積は約0.91となり、病気の人たちのグループのうち91%を正しく「病気」と判断し、残りの9%の達は実際は病気だけれども、「健康」と判断されますね。
同じく、緑の曲線、健康な人達のグループを考えると27の黒い縦線より左の緑色の面積は約0.28、つまり28%の人達は、実際は健康にもかかわらず「病気」と判断されてしまいます。
また、残りの72%の人達は実際は健康で、判断結果も「健康」と正しく判断されます。
| 判定結果 | |||
|---|---|---|---|
| 病気と判断 | 健康と判断 | ||
| 真の状態 | 病気の人グループ | 真陽性 (91%) | 偽陰性 ( 9%) |
| 健康な人グループ | 偽陽性 (28%) | 真陰性 (72%) | |
なので、水色の面積(真陽性:病気の人を「病気」と判断)をなるべく大きくして、緑の面積(偽陽性:健康な人を「病気」と判断してしまう)を小さくすると、識別の性能が高いと言えます。
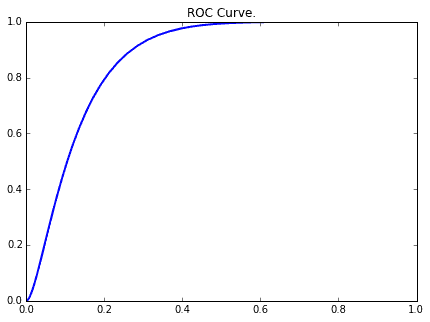
以上のデータからROC曲線を描くと下記のグラフになります。
これがどういうものかを、次項より説明していきます。
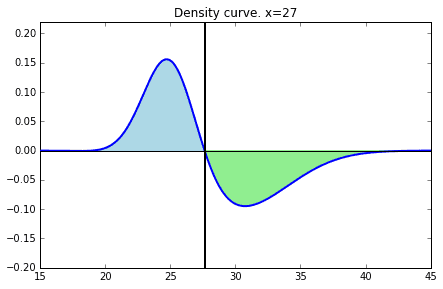
また、今回識別境界をx=27においていますが、これが良い境界であることは最初のグラフの2つの分布を引き算したグラフを描いてみるとわかります。正しい判定(水色面積:病気の人を病気と判断)を増やし、誤った判断(健康な人を病気と判断)を少なくするので、水色の面積は+、緑色の面積はーとなります。水色から緑を引いた曲線を描き、左から順に識別境界を右にずらして考えると、x=27のところより右はマイナスにしかならないので、面積が最大のところは下記のとおりx=27のところということがわかります。
2. ROC曲線の書き方
分布の密度関数、累積密度関数、ROC曲線、と3つのグラフの関係性からまず説明したいと思います。
1段目のグラフは先ほどと同じ病気の人と、健康な人の検査数値の分布です。
識別境界が27の場合、水色の面積が真陽性の割合を表し0.909です。緑の面積が偽陽性の割合で0.280です。
その面積をグラフにしたのが2段目のグラフで、累積密度関数のグラフになっています。1段目の面積と2段目の点が連動しています。
で、3段目はというと、この真陽性=0.909と偽陽性=0.280を1つの点としてプロットしたものになっています。(0.280, 0.909)の点としてプロットしています。
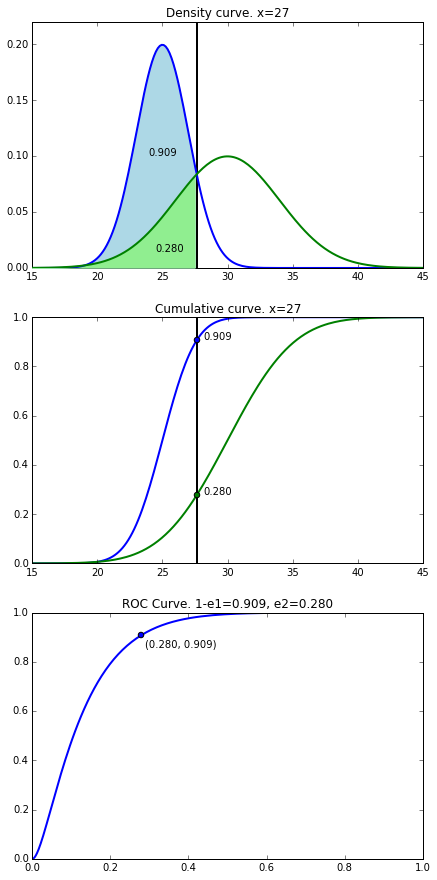
これをさらに分かりやすいようにアニメーションでグラフを書いてみます。この動いている縦線が識別境界を表しており、この線の左側は病気の人と判断、右側は健康な人と判断、というのは前項と同じです。3段目のグラフに着目すると、この動いている点それぞれに対して全てプロットして繋いだ時にできる曲線が3つ目のROC曲線になるのです。
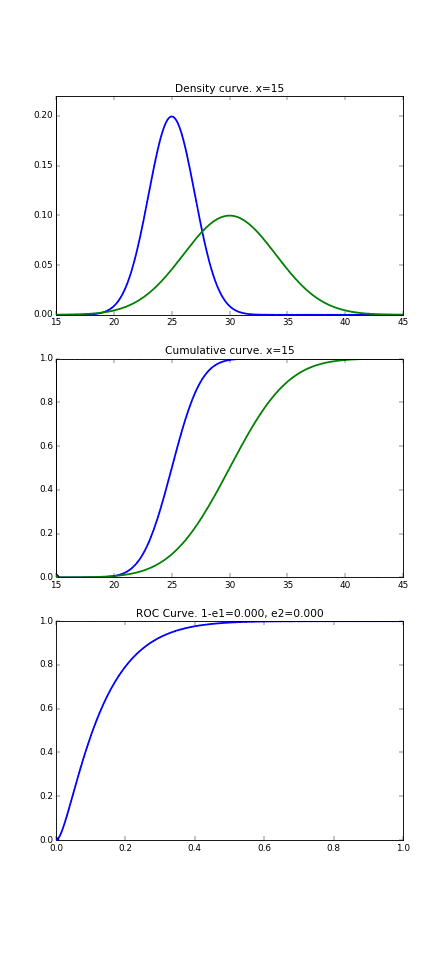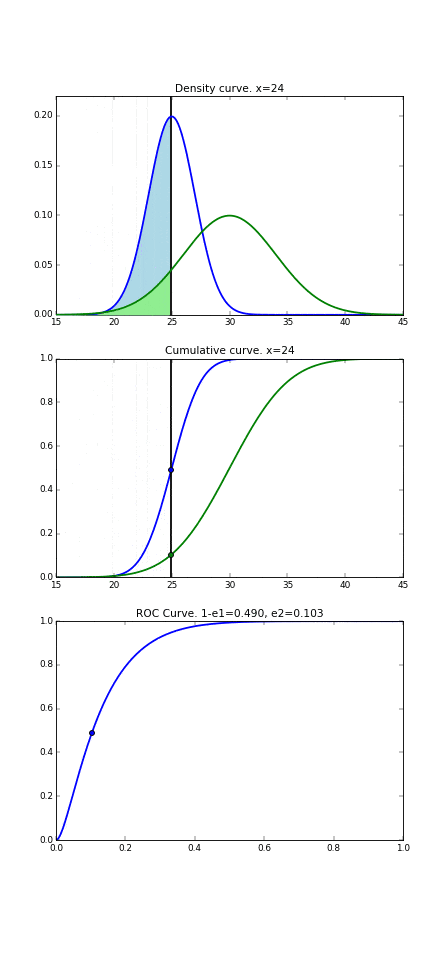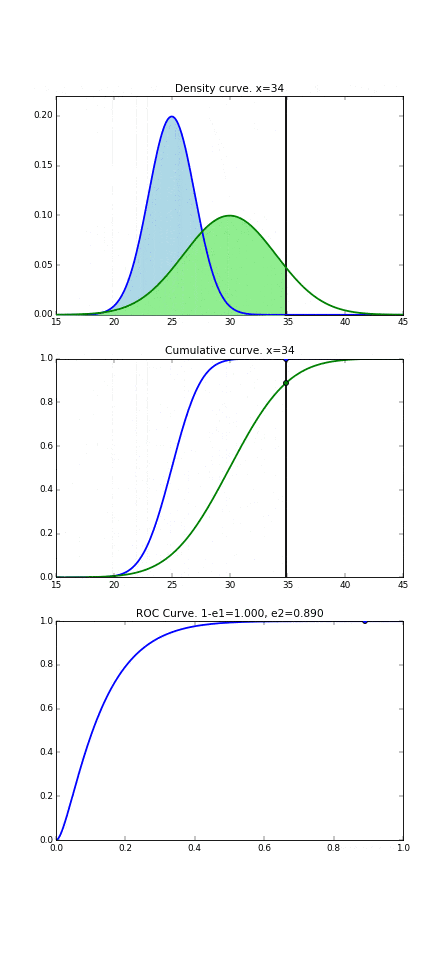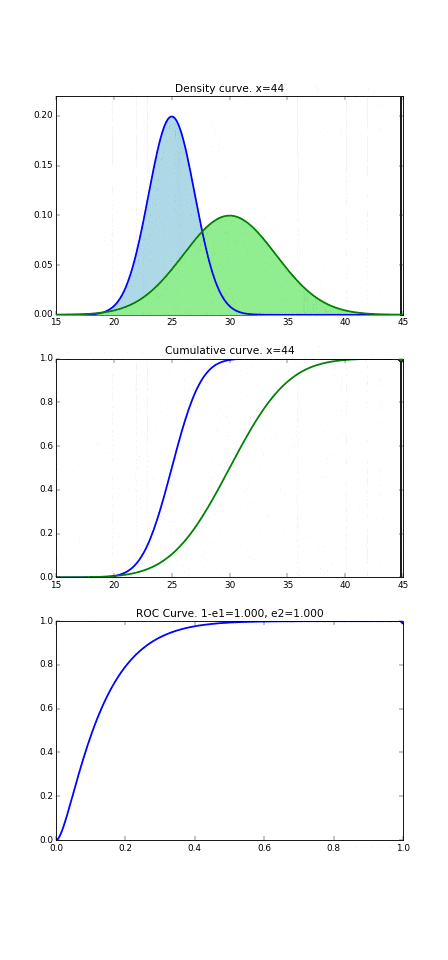
3. ROC曲線の形状の考察
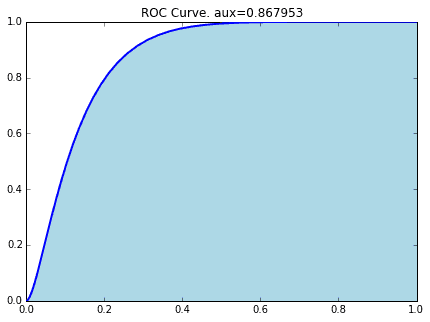
このROC曲線は、2つの密度関数の重なりが少ないほど、形状が左上方向にシフトします。この重なりが少ないほど識別境界の性能が良くなります。この曲線の面積(下記の図の水色の面積)をAUC(Area under the curve)と呼び、曲線が左上にシフトするほど大きくなります。下記の例はAUC=0.867953です。
次にROC曲線の形状が、何によって変化するのかを見ていきます。
最初に、分布の形状が同じで、平均のみ異なる場合です。2つの曲線が完全に一致するときに、ROC曲線が直線になります。
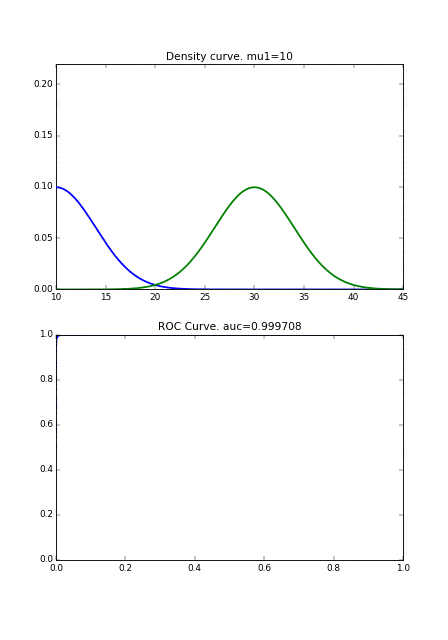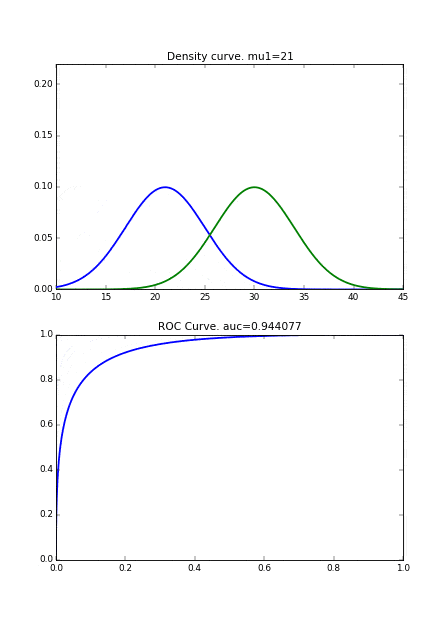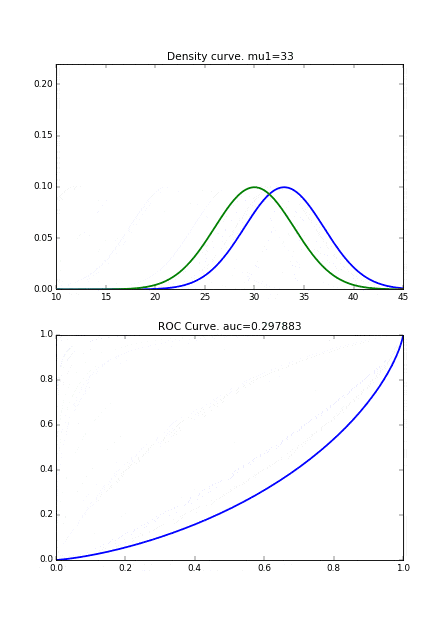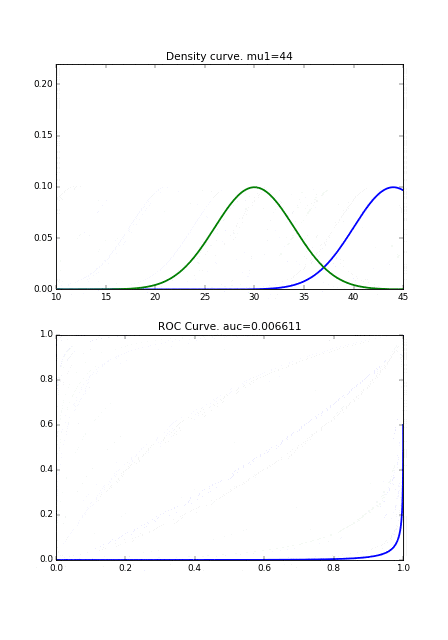
次に分布の形状が異なる場合です。完全に直線にはなりませんが、 2つの曲線同士が近づくとROC曲線が右下にシフトしていることがわかります。
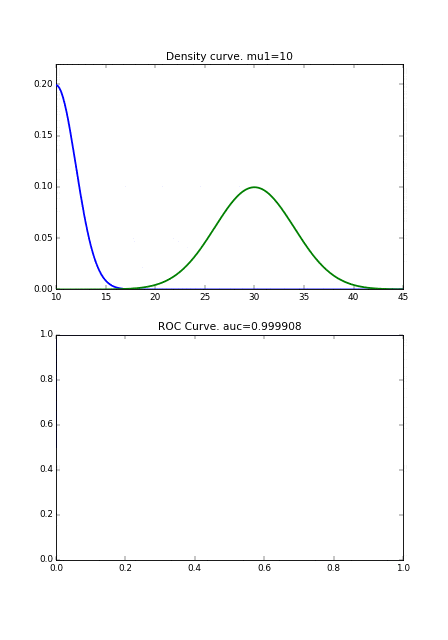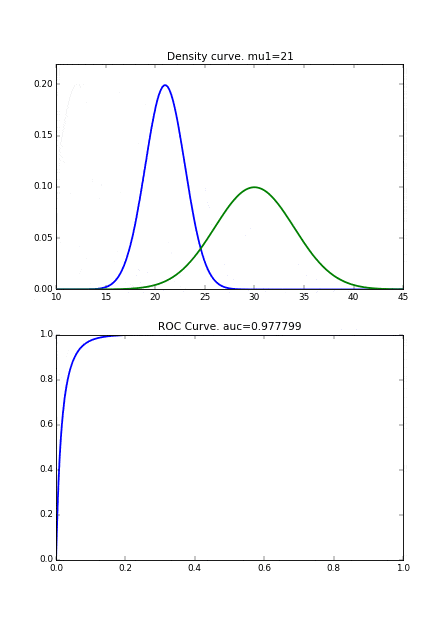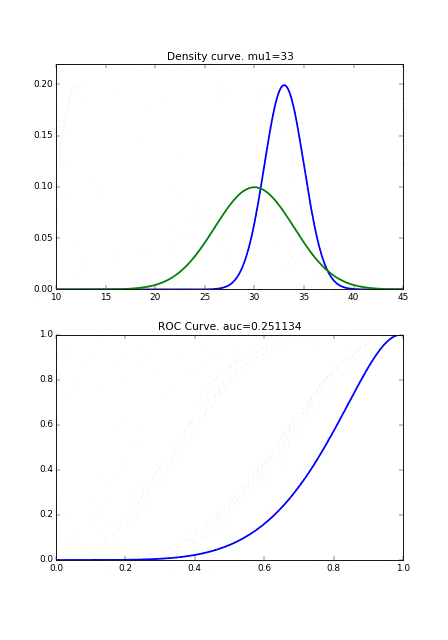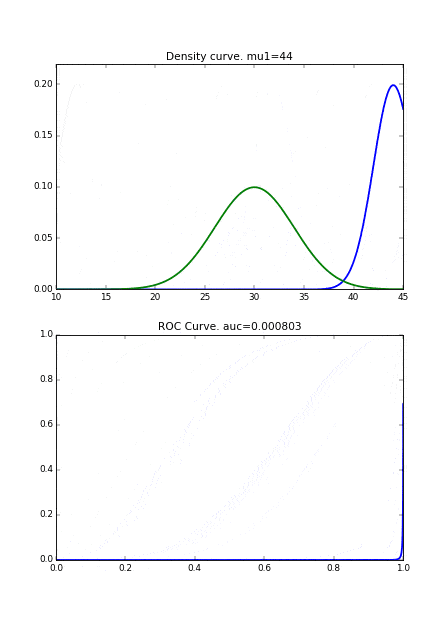
また、もし病気の人の分布の分散が小さければ、それだけ健康な人の分布と重なり合う面積が減るので、それによってもAUCの値が良くなります。
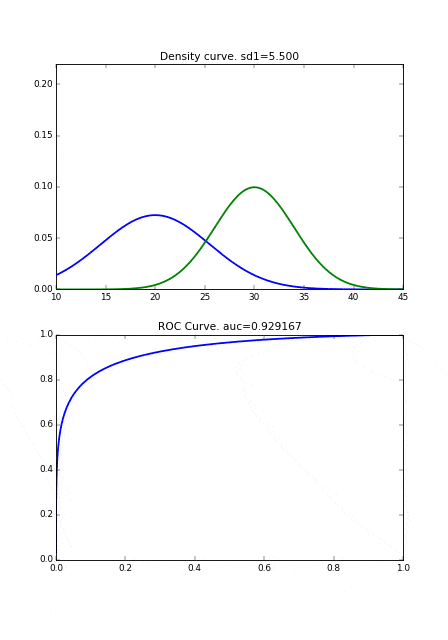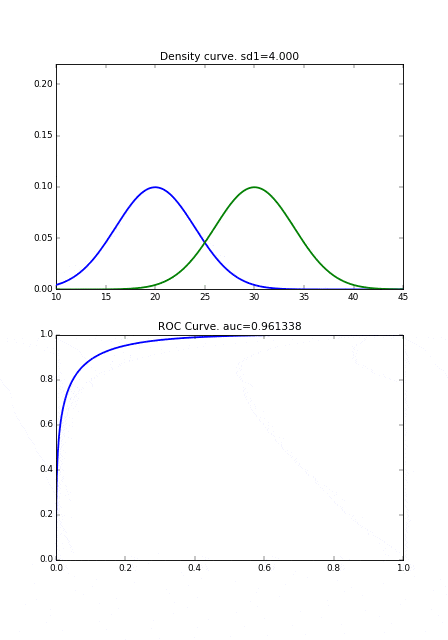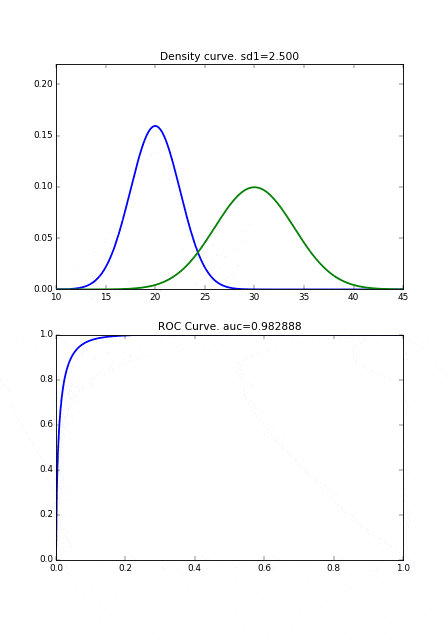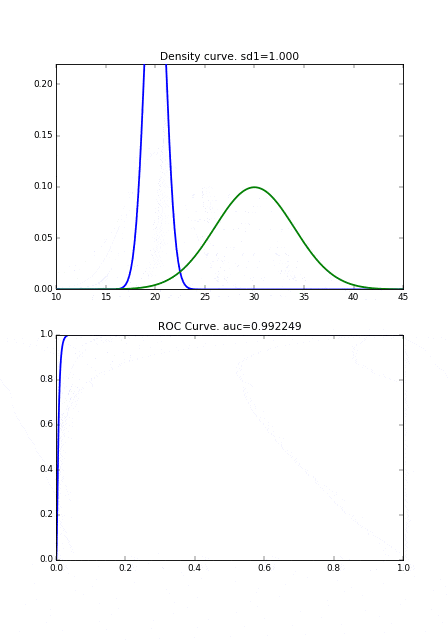
Pythonコード
今回のグラフを書いたPythonコードの一部をGistにアップしています。
###参考###
書籍
「はじめてのパターン認識」平井 有三