今回は前回のROC曲線に続き、統計学検定2級の公式教科書に掲載されている、Q-Qプロットの意味についてアニメーショングラフを用いて解説する記事を書きます。これもちょっとクセのあるグラフといいますか、理解にコツが必要と思いますので解説を試みたいと思います。
RでもqqnormでQ-Qプロットが書けますが、なんだかブラックボックスでその仕組みがイマイチわからないので、Pythonで自力で書いてみました。
1. 今回利用するデータについて#
ということで利用するデータは同教科書にあるマンションの家賃データを使います。
こんなデータです。
Mansion2.data
| Walk_min | distance | Price | Type | Area | Direction | Year | |
|---|---|---|---|---|---|---|---|
| 0 | 8 | B | 7900 | 1K | 30.03 | 南 | 3 |
| 1 | 9 | B | 8500 | 1K | 21.9 | 南 | 5 |
| 2 | 10 | B | 10800 | 1K | 27.05 | 南 | 4 |
| 3 | 10 | B | 10800 | 1K | 29.67 | 南 | 4 |
| ... | ... | ... | ... | ... | ... | ... | ... |
このデータのダウンロードはこちらの統計学検定2級の公式教科書のページ中程にある「ダウンロード用データ」のリンクより行えます。ダウンロードしたzipファイルを解凍し[第2章]-[本文]フォルダにあるMansion2.dataが今回使用するデータです。
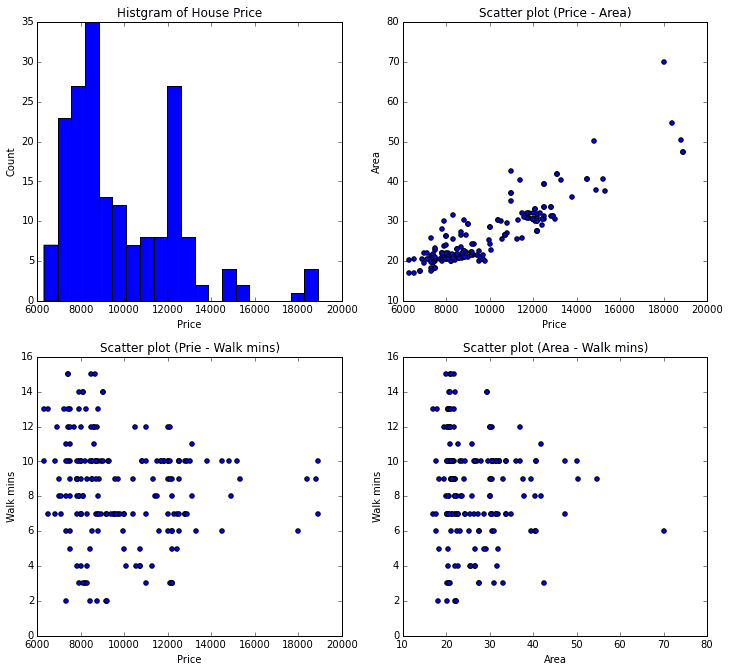
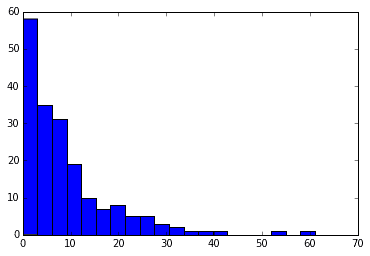
そしてデータを手に入れたらやはり、まずはグラフを書いてデータのイメージをつけたいと思います![]()
価格帯は左側に寄っていて、右に裾が長いタイプのヒストグラムになってます。また、価格と広さには相関がありそうなことが読み取れます。
今回のQ-Qプロットは価格に着目して進めるので、価格についてもう一歩踏み込んでグラフを解釈を試みます。
それは、「この分布が正規分布に従っているか否か」、です。
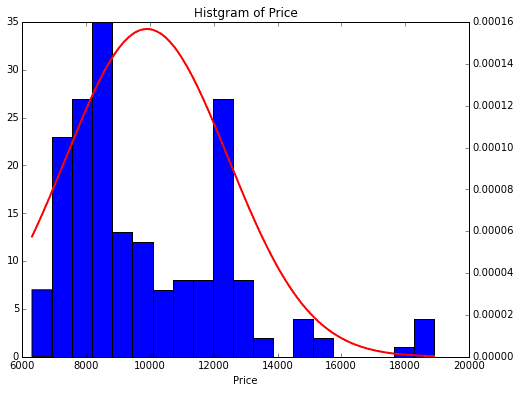
まぁ実は下記の通りこのデータから得られた平均、標準偏差を元に正規分布の密度関数を当てはめてみると明らかに合っていないのですが、それは気にせず進めますw
上記の一連のグラフを描画するPythonコードはこちらです。
2. Q-Qプロットとは何か?
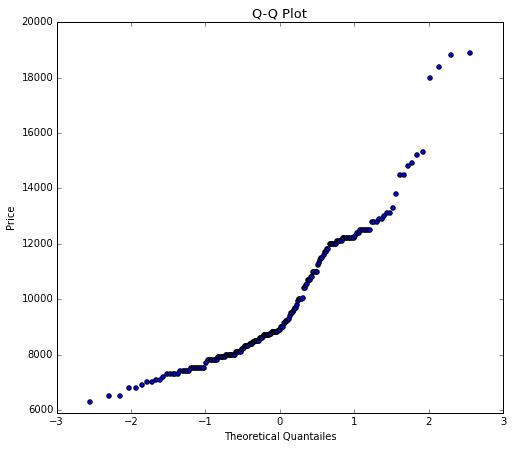
まぁ何はともあれ、Q-Qプロットのグラフそのものを見てみます。
はい、これが今回の対象とするデータ"Price"、つまり家賃のデータに対してQ-Qプロットを作図したものです。ぱっと見、何を示しているグラフかよくわからないですね。
教科書的な説明をすると、「Q-Qプロットとは得られたデータと理論分布を比較し、その類似度を調べるためのグラフ」となります。類似していればプロットした点が直線に並ぶ、そうです。
では、上記のグラフはどう解釈すれば良いのでしょう?
上記のFig.4は、Fig.2の形を変えたものと考えられます。つまり、得られた家賃のデータと、理論分布である正規分布密度関数がどれくらい類似しているかを、直線になっているかどうかの具合で視覚的に理解できるグラフなのです。
3. Q-Qプロットの成り立ち#
さて、このグラフは直線具合で理論分布との類似度を図るということなのですが、なぜそのように言えるかは、このグラフの書き方を理解しないとならないと思いますので、その説明をします。
それではまた家賃データを使って説明していきます。分布の形はこれですね。
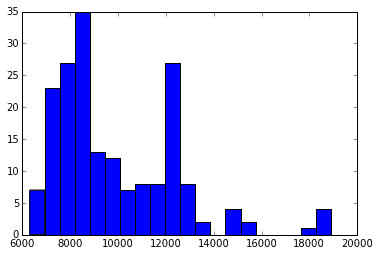
Fig.5
ここからQ-Qプロットを作成するにあたり中間生成物的なグラフを2つ用います。
1つめに使うのが、この家賃データを1つ1つ小さい順に並べて点を打ってグラフを描きます。全部で188個のデータであり、それを0から1の間に均等に並べています。
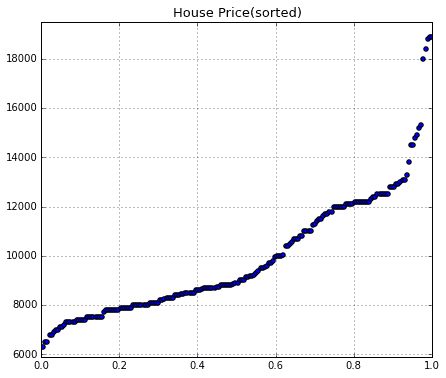
Fig.6
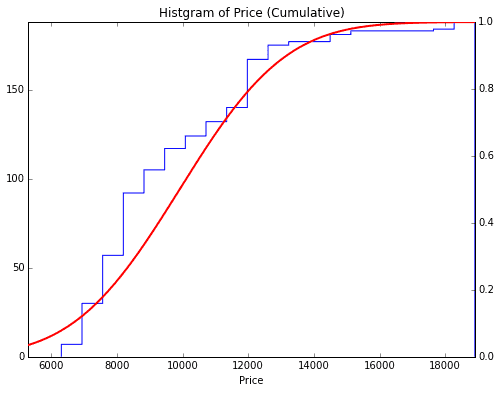
2つめのグラフとして、今回、理論分布として正規分布を仮定するので、正規累積分布関数のグラフを書いて使います。これも、家賃データと同数の188個の点で累積密度関数を表現します。
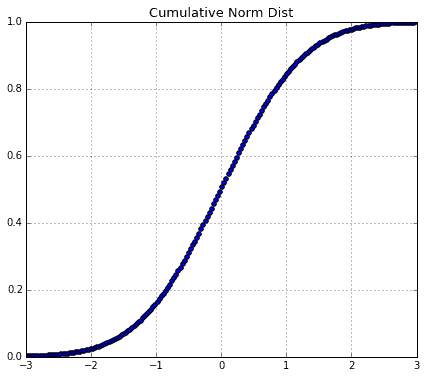
Fig.7
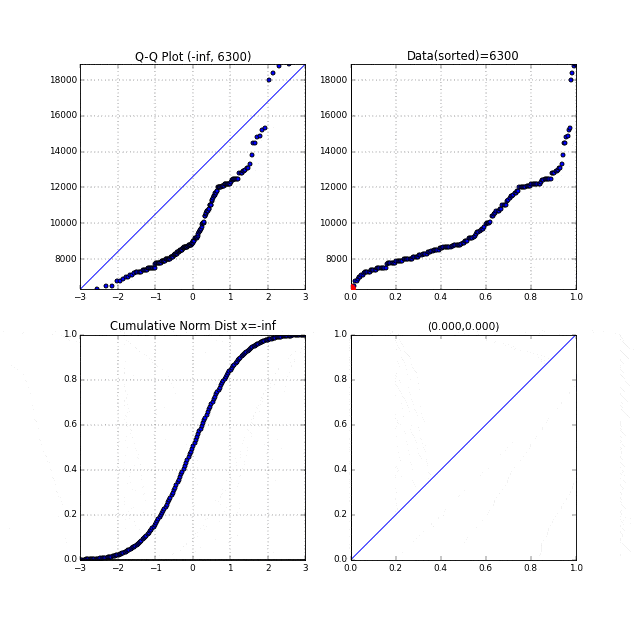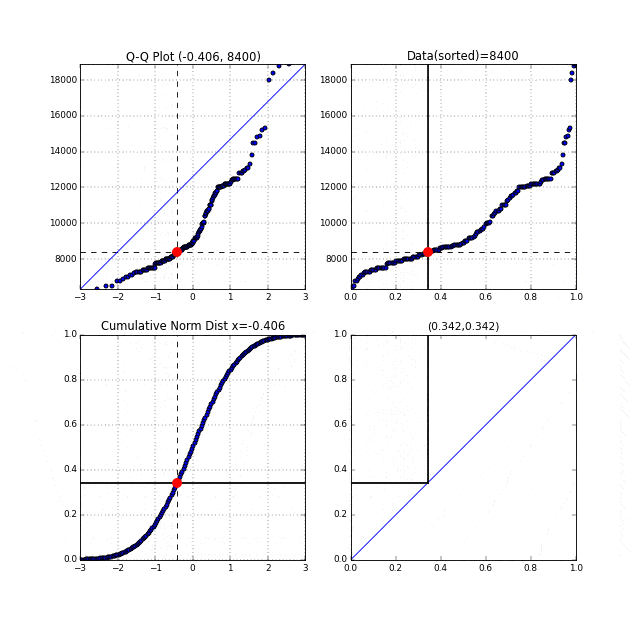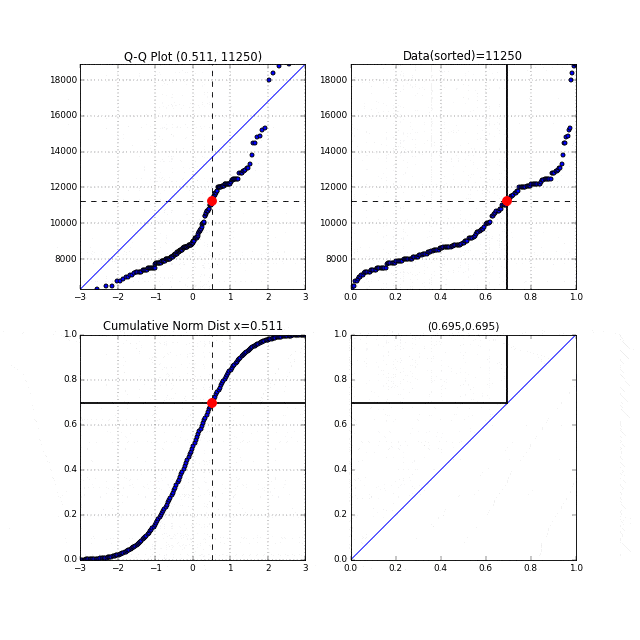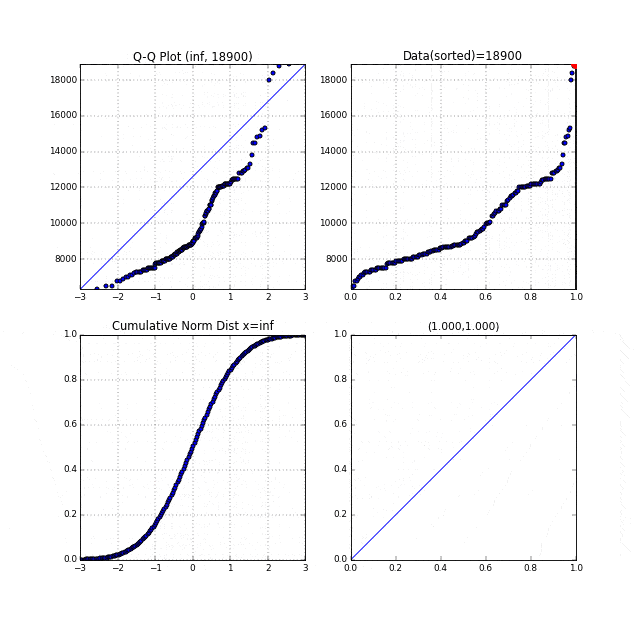
この2つのグラフを組み合わせることで、Q-Qプロットのグラフが書けるのです。それをアニメーショングラフで見てみましょう。
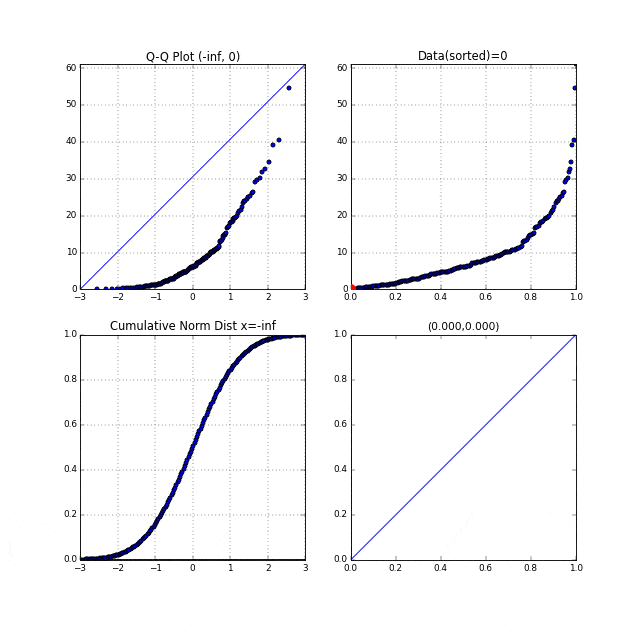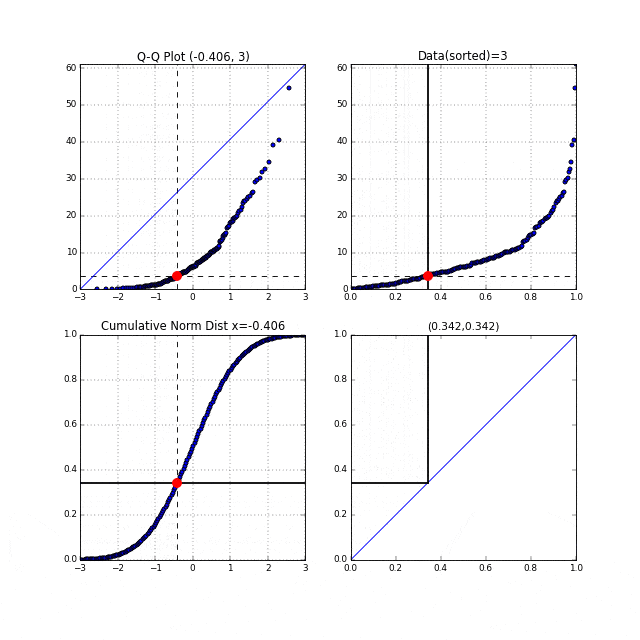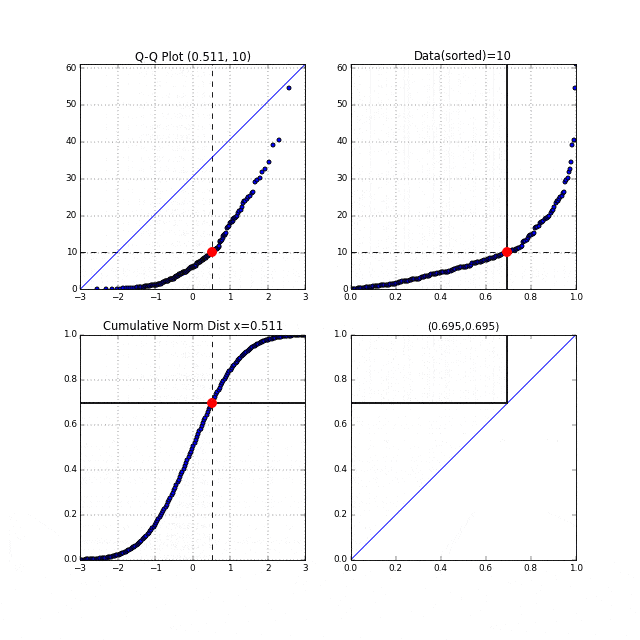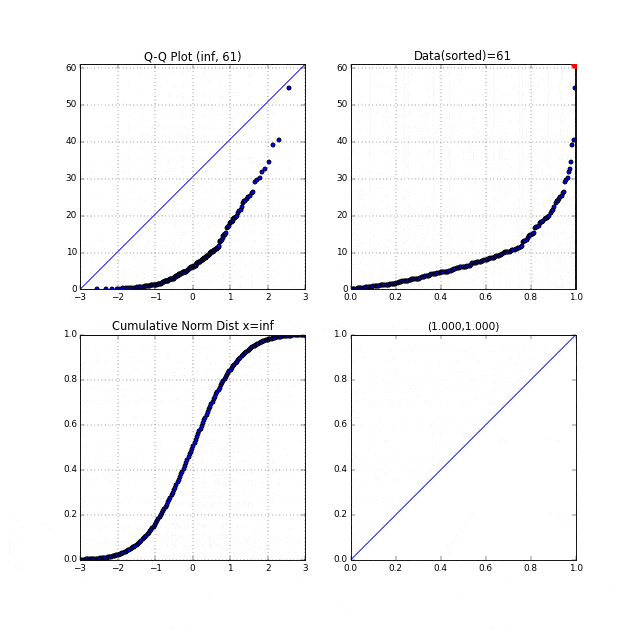
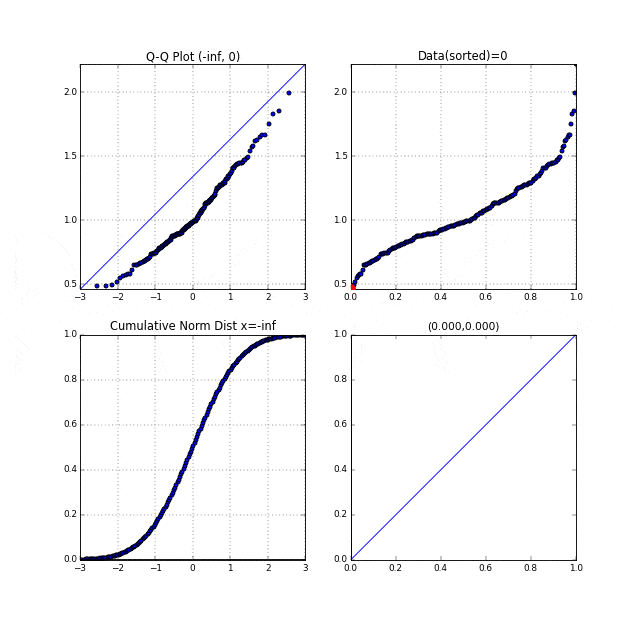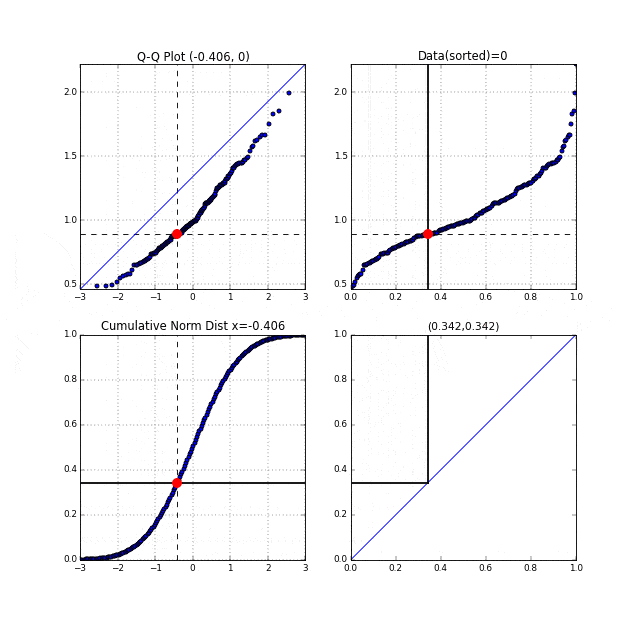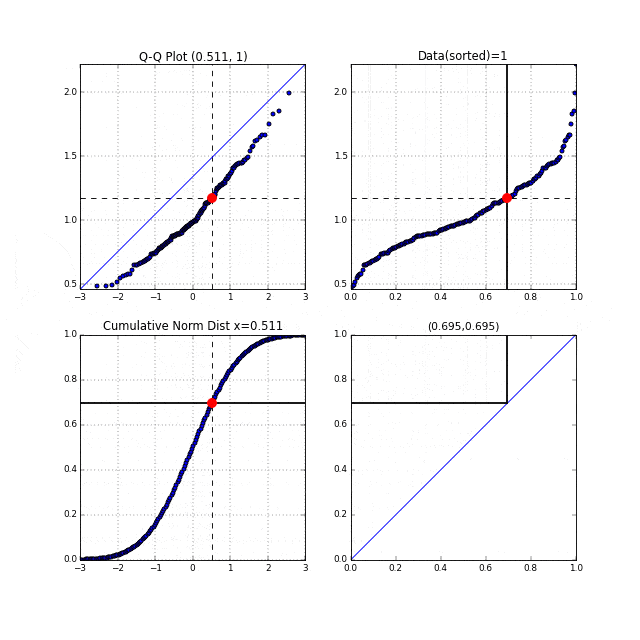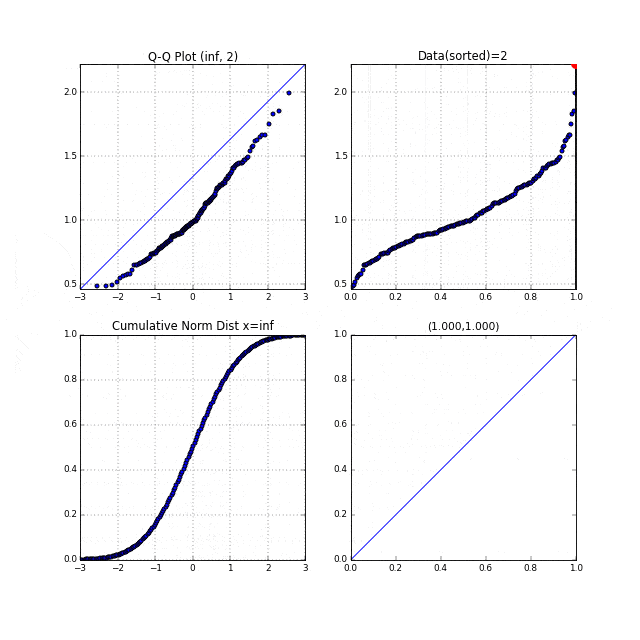
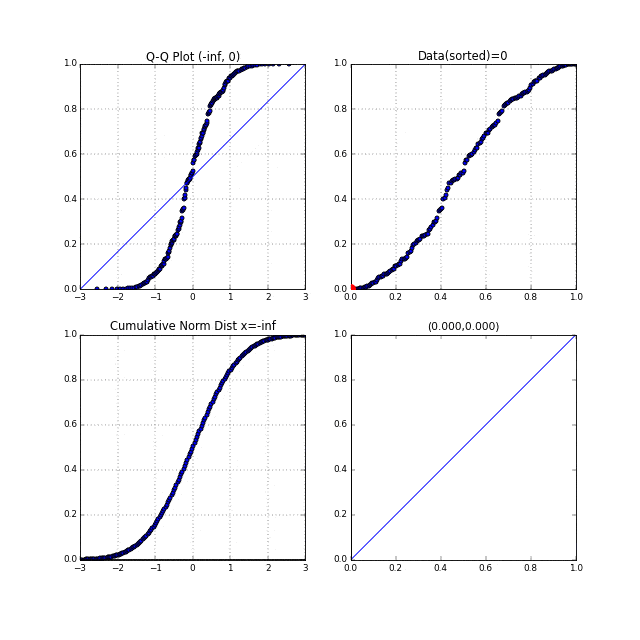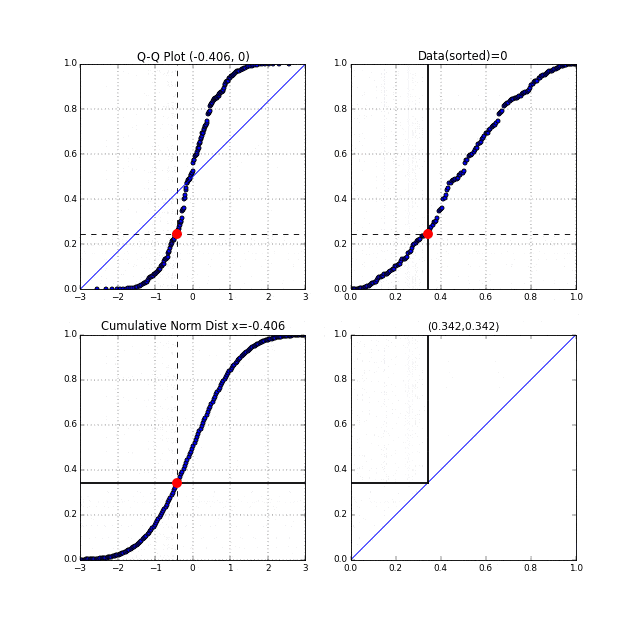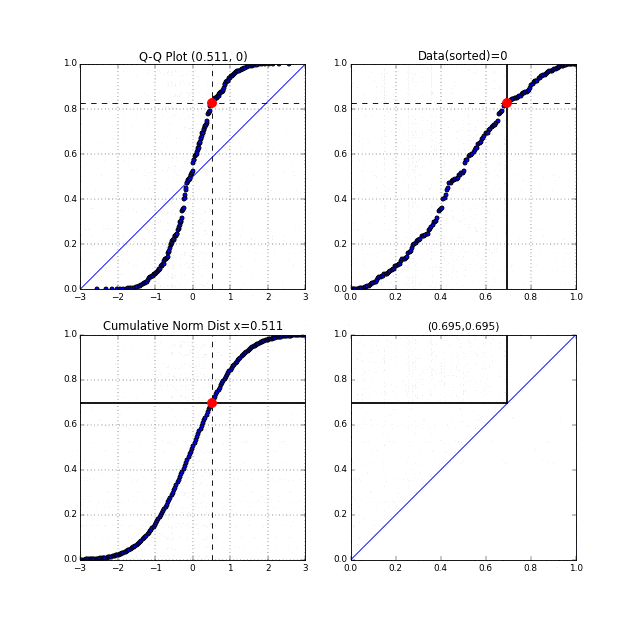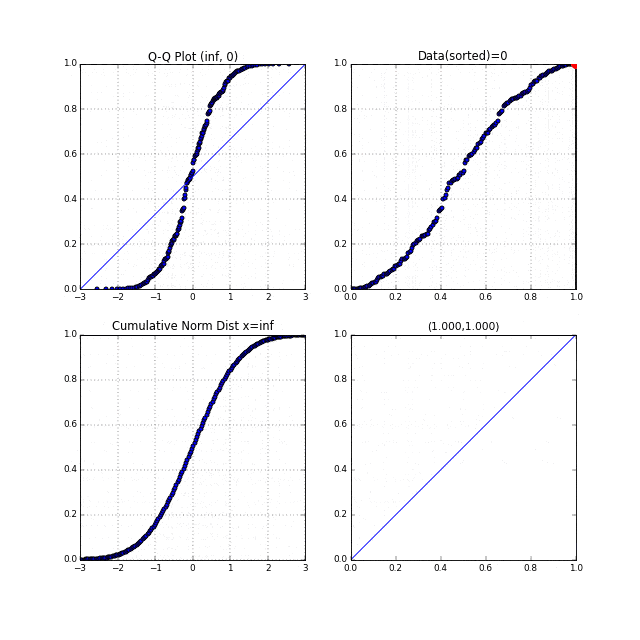
先ほどの中間生成物グラフFig.6が右上, Fig.7が左下のグラフにあたります。左上がターゲットとなるQ-Qプロットです。まず右上の家賃データのグラフの横軸は分位数を表しており、同じく左下の正規累積分布関数の縦軸も分位数を表しています。右上、左下それぞれの、この分位数を同時に0から1に向かってスライドさせます。それを黒い線が表しています。黒い線と交わっている点を赤い点で表示しています。この赤い点同士を同時にプロットしたものがQ-Qプロットなのです。点線がそれを表しています。
このQ-Qプロットの"Q"とはQuantile"(分位数)を表しており、右上、左下のグラフの分位数を同時に動かしていることからこの名前が付いているのだと思います。
(Pythonコードはこちら)
4.正規分布に従う乱数のQ-Qプロット#
さて、データと理論分布が同じ場合Q-Qプロットは直線になるということでしたので、これも試してみたいと思います。ということは、正規分布に従う乱数を使うということですね。
正規分布に従う乱数188個をヒストグラムにしたものがこちらです。
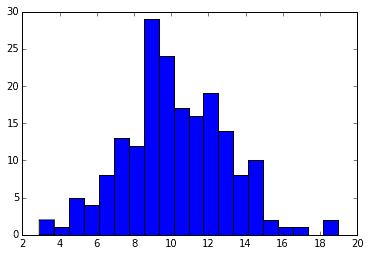
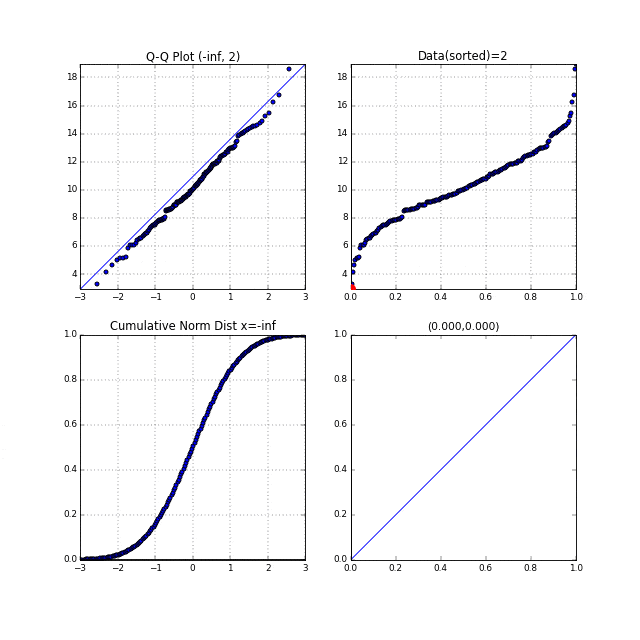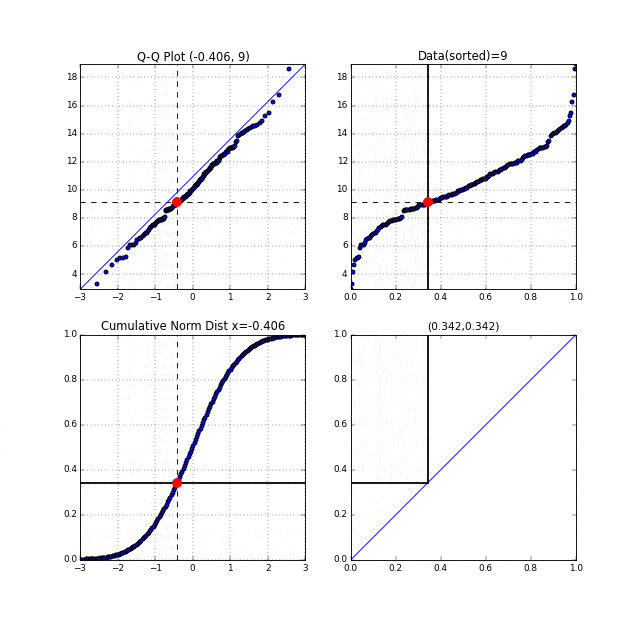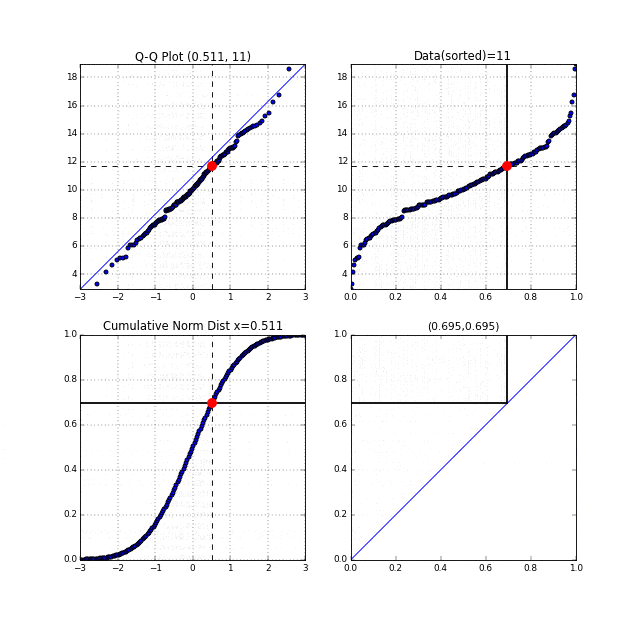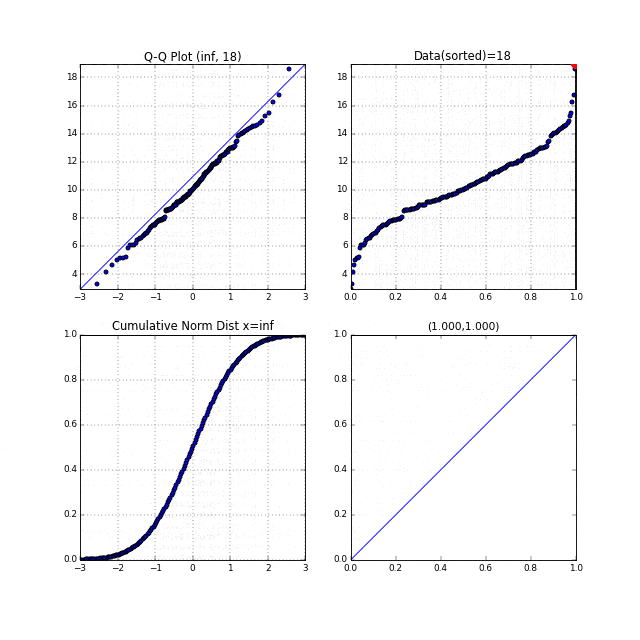
さらにQ-Qプロットを描いてみると・・・
確かに直線になっていますね ![]()
5.指数分布に従う乱数のQ-Qプロット#
このような形状の場合、正規Q-Qプロットは右下に凸な形になります。
6.F分布に従う乱数のQ-Qプロット#
ちょっとだけ右に裾が長いタイプのF分布です。
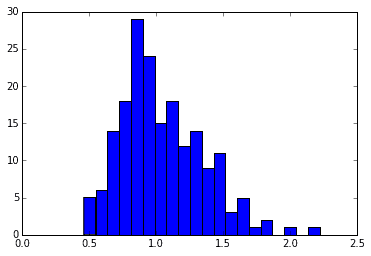
これも、ちょっとだけ、右下に凸なQ-Qプロットが描けています。
6.β分布に従う乱数のQ-Qプロット#
次に左に裾が長いタイプの分布、$\alpha=6, \beta=2$のベータ分布を用いてQ-Qプロットを書いてみます。
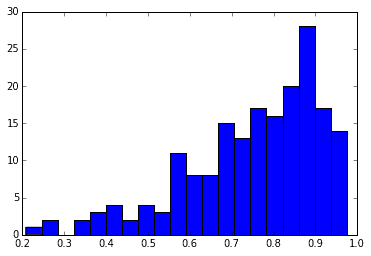
今度は逆に左上に凸なQ-Qプロットが描けています。
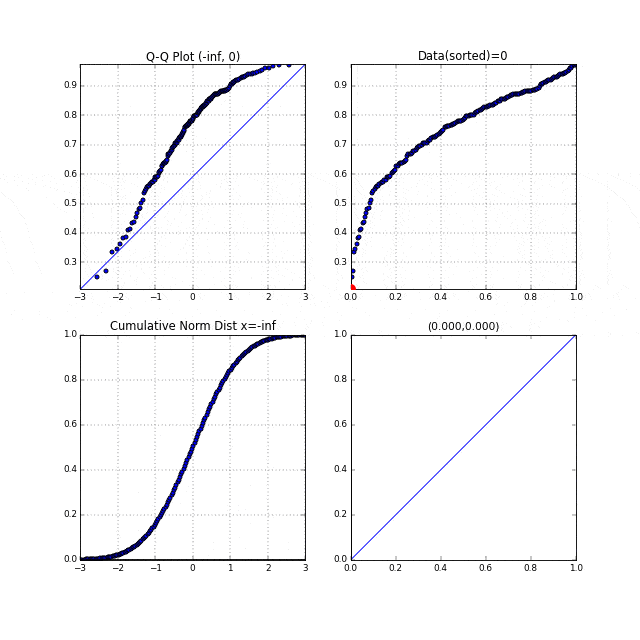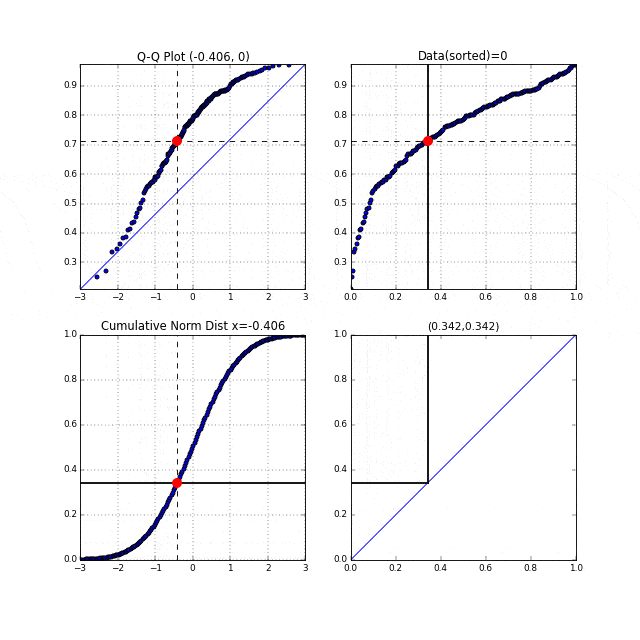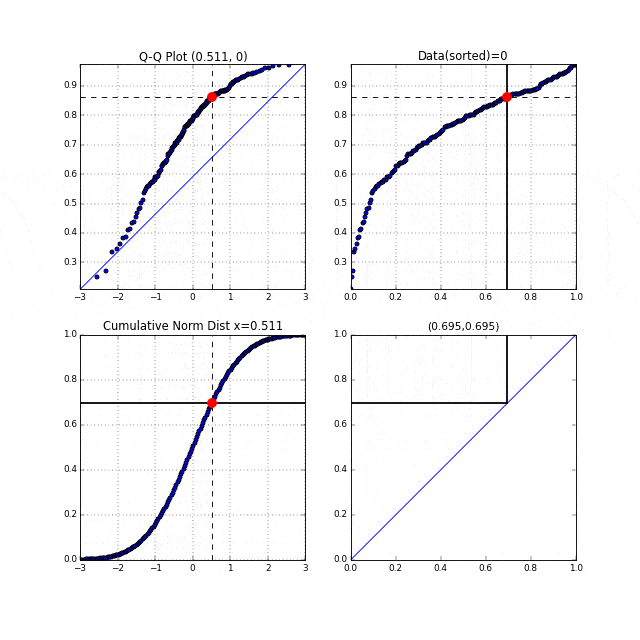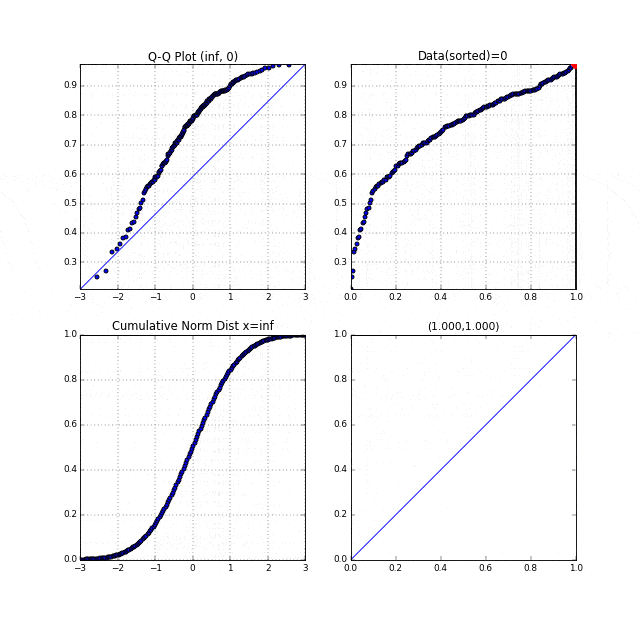
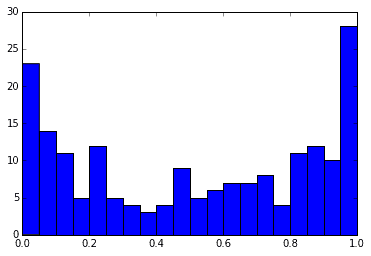
ちょっと変わりどころだと、$\alpha=0.5, \beta=0.5$のベータ分布で、両サイドに頂点があるような分布です。この場合途中まで右下に凸、後半は左上に凸、というQ-Qプロットが描けています。
このページで記載しているグラフを描画するPythonコードの全文はこちら