はじめに
Pythonを使って学ぶデリバティブシリーズの第二弾。
だいぶ間があいてしまったけど、オプションプライシングくらいまでは続けていくつもり。
第1弾をまだ見てない方は良ければ覗いてください。
Pythonを使って学ぶデリバティブシリーズ
第1弾: フォワード為替レートの算出-
第2弾: イールドカーブを引く(JPYLiborカーブ)
今回の内容
シンプルなイールドカーブの引き方について書く。
担保やテナースプレッド、ベーシススプレッドといったことはここでは考慮しない。マルチカーブではなくシングルカーブの世界。
今回はまずは円のカーブ。次回はドルを書くつもり。
カーブの引き方
ブートストラップ法以外にもカーブの引き方はあるが、
ここではブートストラップ法を解説する。
あと本当は日数計算方式(1年を360日や365日とするのかなど)や休日などを考慮する必要があるが、
ここでは気にしない。使うレートをキャッシュレートとスワップレートのみとする。
ブートストラップ法でのカーブの引き方
円金利スワップの場合、変動側は6ヶ月Libor、固定側は6ヶ月固定金利による交換となる。
現時点をt、
満期をT、
時点t満期TのスワップレートをS(t, T)、
時点t満期TのディスカウントファクターをDF(t, T)とした場合
固定金利側の現在価値P(t)は
P(t) = \frac{1}{2}S(t,T) \times DF(t, t_{0.5}))
+ \frac{1}{2}S(t,T) \times DF(t, t_{1.0}))
+ ...
+ \frac{1}{2}S(t,T) \times DF(t, T))
となる。
変動金利側の現在価値F(t)は
F(t) = \frac{1}{2}f(t, t_0, T_{0.5}) \times DF(t, t_{0.5})
+ \frac{1}{2}f(t, t_{0.5}, T_{1.0}) \times DF(t, t_{1.0})
+ ...
+ \frac{1}{2}f(t, T-0.5, T) \times DF(t, T)
となる。
ここでのf(t, t1, t2)は時点tにおける時点t1スタートで時点t2満期の円フォワードレートを表す。
金利スワップ契約が成立するのは、固定側の現在価値と変動側の現在価値が等しいときであるため、
P(t) = F(t)
が成り立つ。
そして、実際の金利スワップでは想定元本が等しく元本交換は行わないが、便宜的に想定元本1を考慮すると以下のような式になる。
\frac{1}{2}S(t,T) \times DF(t, t_{0.5}))
+ \frac{1}{2}S(t,T) \times DF(t, t_{1.0}))
+ ...
+ \frac{1}{2}S(t,T) \times DF(t, T))
+ 1 \times DF(t, T) \\
=
\frac{1}{2}f(t, t_0, T_{0.5}) \times DF(t, t_{0.5})
+ \frac{1}{2}f(t, t_{0.5}, T_{1.0}) \times DF(t, t_{1.0})
+ ...
+ \frac{1}{2}f(t, T-0.5, T) \times DF(t, T)
+ 1 \times DF(t, T)
右辺はフォワードレートを元本を現在価値に戻しているだけであるため値は1である。
(補足)なぜ1?
額面100のLibor変動利付債を考えるみる。
購入時のキャッシュアウトの100と償還時(将来)のキャッシュイン100とLiborによりクーポンの価値は等価となる。
つまり、想定元本を1とした場合、Libor変動金利と元本1をそれぞれ割り引いたものは1となる。
そのため、
\frac{1}{2}S(t,T) \times DF(t, t_{0.5}))
+ \frac{1}{2}S(t,T) \times DF(t, t_{1.0}))
+ ...
+ \frac{1}{2}S(t,T) \times DF(t, T))
+ 1 \times DF(t, T)
= 1
となる。
この式を用いて満期の短いものから逐次的にDFを求めていくのがブートストラップ法。
長々と書いたけど、ブートストラップ法自体は
名前のとおり手前の結果を使ってその後の結果を逐次的にといていくこと。
では、実際に逐次的にDFを算出していく。
1年以内のDF算出
逐次的にDFを算出していくと言ったが、1年以内はLibor金利、俗にいうキャッシュレートを使ってDFを算出するため、金利から直接DFを算出できる。
0.5年時点でのDFの算出
0.5年時点でのDF算出には6ヶ月Liborを使用する。
また、計算は単利計算で行う。
DF(t, t_{0.5}) = \frac{1}{(1 + r(t, t_{0.5}) \times \frac{1}{2})}
ここでの、r(t, T)は時点tでの満期Tの円Libor金利を表す。
1年時点でのDFの算出
1年時点でのDF算出には12ヶ月Liborを使用する。(1Yスワップレートを使う場合もある)
DF(t, t_{1.0}) = \frac{1}{(1 + r(t, t_{1.0}))}
まとめ
Libor金利(キャッシュレート)を使う1年までのDFは以下の式で算出可能。
DF = \frac{1}{1 + r(t) * t / 100} \\
r(t): t時点でのLibor金利(\%から実数に要変換) \\
t: 年数 \\
1年超のDF算出
ここからがDFを逐次的に求めていく話。
市場から取得したLibor Swap金利、俗にいうスワップレートを0.5年刻みで補完したうえで前述したブートストラップ法の式で算出していく。
なぜ0.5年刻みかというと、想定している円金利スワップのクーポンが半年ロールであるため
1.5年時点のDFの算出
ブートストラップ法の式において、1.5年時点を考えた場合
\frac{1}{2}S(t, t_{1.5}) \times DF(t, t_{0.5}))
+ \frac{1}{2}S(t, t_{1.5}) \times DF(t, t_{1.0}))
+ \frac{1}{2}S(t, t_{1.5}) \times DF(t, t_{1.5}))
+ 1 \times DF(t, t_{1.5})
= 1
となる。(ブートストラップ法で導いた式を1.5年で止めた形)
ここで未知の変数はDF(t, t_{1.5})のみである。
そのため、
DF(t, t_{1.5}) = \frac{ 1 - ( DF(t, t_{0.5}) + DF(t, t_{1.0}) ) \times \frac{S(t, t_{1.5})}{2}}{ 1 + \frac{S(t, T_{1.5})}{2} }
となり、1.5年のDFが算出できる。
2年時点のDFの算出
満期2年時点でのDFについても同様に、
\frac{1}{2}S(t, t_{2.0}) \times DF(t, t_{0.5}))
+ \frac{1}{2}S(t, t_{2.0}) \times DF(t, t_{1.0}))
+ \frac{1}{2}S(t, t_{2.0}) \times DF(t, t_{1.5})) \\
+ \frac{1}{2}S(t, t_{2.0}) \times DF(t, t_{2.0}))
+ 1 \times DF(t, t_{2.0})
= 1
とできることから、
DF(t, t_{2.0}) = \frac{ 1 - ( DF(t, t_{0.5}) + DF(t, t_{1.0}) + DF(t, t_{1.5}) ) \times \frac{S(t, t_{2.0})}{2}}{ 1 + \frac{S(t, T_{2.0})}{2} }
となり、算出できる。
まとめ
Libor Swap金利(スワップレート)を使う1年超の期間のDFはブートストラップ法を用いる場合、以下の式で算出可能。
DF(t, T) = \frac{ 1 - \sum_{i=0.5}^{T-0.5}DF(t, t_i) \times \frac{S(t, T)}{2}}{1 + \frac{S(t,T)}{2}} \\
(T > 1)
ゼロレートの算出
算出したDFより連続金利ベース(ゼロレート)を算出することが可能。
y(t, T) = \frac{ \ln DF(t, T) }{ -(T - t) }
DF(t, T) = e^{-rτ}の変形
τ: 期間(T - t)
r: t時点から満期Tまでのスポットレート金利(ゼロレート、y(t,T)のこと)
y(t, T)は時点t満期Tの連続金利ベースのゼロレートを表す。
求めた満期以外のゼロレートについてはDFを線形補間やスプライン補間などして算出する。
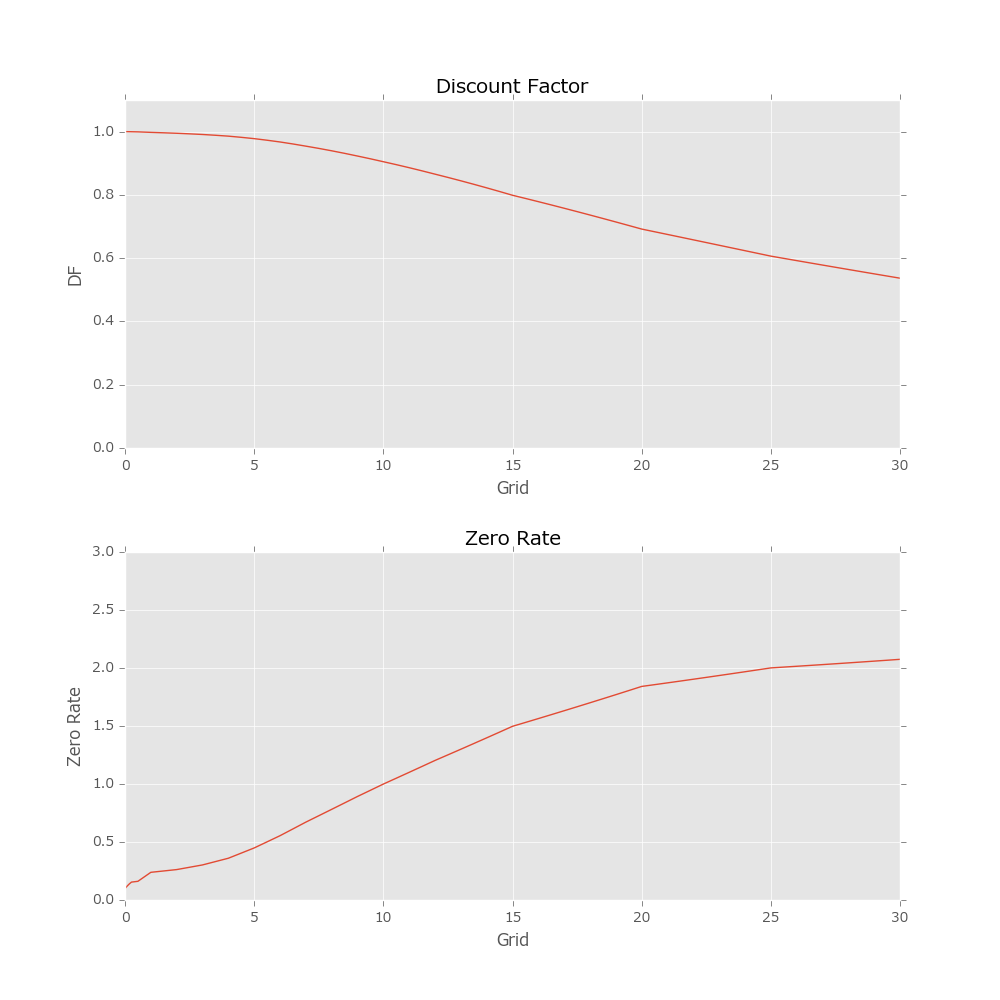
算出したゼロレートをプロットすればカーブがひける。
補足
ゼロレートとパーレート
ゼロレートとは複利ベ-スの割引債(ゼロクーポン債)の最終利回りのこと。
割引債は、満期日にのみキャッシュ・フローが発生する金融商品。
ゼロレートは現時点から始める金利であり、フォワードレートとは区別するために、スポットレートとも呼ばれる。
ゼロレートは途中の利払いが無く、再運用の問題が発生しないことから、将来のキャッシュフローを現在価値に割り引く際に用いられる。
パーレートとは複利ベースの利付債の最終利回りのこと。
利付債は、満期までの間に毎年一定の利子支払いが発生する金融商品。
DFの算出式
6ヶ月利払いとかおいておいて一般化すると
DF_i = \frac{1 - r_i \sum_{k=1}^{i-1} DF_{i-1}}{ 1 + r_i} \\
i: 時点 \\
r_i: 時点iにおける金利 \\
DF_i: 時点iにおけるディスカントファクター \\
イールドカーブを引くプログラム
長くなったけど最後にPythonで実際にカーブをひいてみる。
他通貨やマルチカーブを引くときに諸々書き直すと思われるが、一旦動くので良しとする。(言い訳?)
処理の流れ
- インプットとなるマーケットデータを読み込む(この時に期間を年日数に変換している)
- 半年ロールのため、スワープレートがないグリッドは線形補間してデータを用意する
- DFの算出を算出する(1年までと1年超で算出ロジックを分岐)
- DFからゼロレートを算出
- DFやゼロレートをプロット
プログラム
# -*- coding: utf-8 -*-
# グラフ化に必要なものの準備
import matplotlib
import matplotlib.pyplot as plt
# データの扱いに必要なライブラリ
import numpy as np
from scipy import interpolate
# その他
from enum import Enum
# matplotlibのおまじない
plt.style.use('ggplot')
font = {'family': 'meiryo'}
matplotlib.rc('font', **font)
# 諸データ
# JPY Libor
cash_rate = {
"ON": 0.1, "1W": 0.10357, "1M": 0.12014, "2M": 0.13857, "3M": 0.15429, "6M": 0.16123, "12M": 0.23875
}
# JPY Libor Swap
swap_rate = {
"2Y": 0.26250, "3Y": 0.30250, "4Y": 0.36000, "5Y": 0.44813, "6Y": 0.55250,
"7Y": 0.66750, "8Y": 0.77500, "9Y": 0.88250, "10Y": 0.98500, "12Y": 1.17750, "15Y": 1.44750, "20Y": 1.75000,
"25Y": 1.89000, "30Y": 1.95813
}
input_market_data = cash_rate.copy()
input_market_data.update(swap_rate)
class RateType(Enum):
CASH_RATE = 1
SWAP_RATE = 2
class MarketData:
def __init__(self, grid, rate):
self.grid = grid
self.rate = rate / 100 # 入力の%を実数に
self.set_term()
self.set_rate_type()
def set_term(self):
if self.grid == "ON":
self.term = 1 / 365
else:
num = float(self.grid.replace("M", "").replace("W", "").replace("Y", ""))
if "W" in self.grid:
self.term = num * 7 / 365
elif "M" in self.grid:
self.term = num * 1 / 12
elif "Y" in self.grid:
self.term = num
else:
self.term = 0.0
def set_rate_type(self):
if self.term <= 1:
self.rate_type = RateType.CASH_RATE
else:
self.rate_type = RateType.SWAP_RATE
def value(self):
print("Grid:{0}, RateType: {1}, Term:{2}, Rate: {3}".format(self.grid, self.rate_type, self.term, self.rate))
class YieldCurve:
def __init__(self, market_data_list):
self.market_data_list = market_data_list
self.sigma_df = 0.0 # TODO:もっとうまいことやる
self.df_list = []
self.zero_list = []
def get_grids(self):
return list(map(lambda x: x.term, self.market_data_list))
def interpolate_swap_rate(self):
i = 1.5 # 1Y以降、JPYは半年ロールのため1.5からスタート
original_rates = list(map(lambda x: x.rate * 100, self.market_data_list))
f = interpolate.interp1d(self.get_grids(), original_rates)
while i <= 30:
r = list(filter(lambda x: x == i, self.get_grids()))
if not r:
m = MarketData(str(i) + "Y", f(i))
self.market_data_list.append(m)
i += 0.5 # JPYは半年ロールのため+0.5
# 最後にソートしておく
self.market_data_list.sort(key=lambda x: x.term)
def output_market_data_list(self):
for mkt in self.market_data_list:
mkt.value()
def generate_curve(self):
for mkt in self.market_data_list:
self.calc_df(mkt)
def calc_df(self, mkt):
if mkt.rate_type == RateType.CASH_RATE:
d = 1 / (1 + mkt.term * mkt.rate)
self.df_list.append(d)
elif mkt.rate_type == RateType.SWAP_RATE:
# 半年ロールのグリッドのDFのみの合計
d = (1 - self.sigma_df * mkt.rate / 2) / (1 + mkt.rate / 2)
self.df_list.append(d)
if mkt.term % 0.5 == 0:
self.sigma_df += d
self.calc_zero(mkt, d)
def get_df(self, term):
f = interpolate.interp1d(self.get_grids(), self.df_list, kind="cubic")
return f(term)
def calc_zero(self, mkt, d):
if mkt.rate_type == RateType.CASH_RATE:
self.zero_list.append(mkt.rate)
elif mkt.rate_type == RateType.SWAP_RATE:
zero = -1 * np.log(d) / mkt.term
self.zero_list.append(zero)
def output(self):
print("Grid: DF: ZeroRate:")
for i, v in enumerate(self.market_data_list):
print("{0}: {1}: {2}".format(v.grid, self.df_list[i], self.zero_list[i] * 100))
def plot(self):
fig = plt.figure(figsize=(10, 10))
ax_df = fig.add_subplot(2, 1, 1)
plt.subplots_adjust(hspace=0.3)
ax_df.set_ylim([0, 1.1])
ax_df.plot(self.get_grids(), self.df_list)
ax_df.set_title("Discount Factor")
ax_df.set_xlabel("Grid")
ax_df.set_ylabel("DF")
ax_zero = fig.add_subplot(2, 1, 2)
ax_zero.set_ylim([0, 3])
ax_zero.plot(self.get_grids(), list(map(lambda z: z * 100, self.zero_list)))
ax_zero.set_title("Zero Rate")
ax_zero.set_xlabel("Grid")
ax_zero.set_ylabel("Zero Rate")
plt.show()
if __name__ == '__main__':
# read market data
market_data_list = list(map(lambda x: MarketData(x[0], x[1]), input_market_data.items()))
# generate yield curve
curve = YieldCurve(market_data_list)
curve.interpolate_swap_rate()
curve.generate_curve()
curve.plot()
参考書籍
EXCELでわかるLIBORディスカウントとOISディスカウント
最後に
詳しくないけど、業務ではもっと色々考慮してちゃんとカーブを引いています。