概要
2016年の流行語大賞も獲得したポケモンGO ![]()
みなさんもたくさんポケモンを捕まえて遊びましたか ![]()
さてポケモンGOでは、
- 体重
- 身長
- CP
- ワザ
といった**捕まえたポケモンごとに異なる特徴の値 = 個体値(個体ごとに異なる値)**が存在します。
ぼくは前々から、これらの個体値がどのように分布しているのか、あるいはそれらの間に何か関係があるのかが気になっていました。
まぁただ単純に調べてみたかったというそれだけなのですが(汗)
そこでこの記事では、自分が実際に捕まえたコイキングの個体値のデータを使い、CP / 体重 / 身長の各パラメータ間に相関はあるのか(無いと言えるか)という疑問を無相関検定で確かめています ![]()
本記事ではあくまで**「身近なデータを使って統計分析ができるよ~」ということを楽しくお伝えしたいという趣旨で書いていますので、難しい用語や考え方は極力避けているつもりです。**
最近はデータサイエンス方面も盛り上がっていて、こういった分析に興味がある方もいると思うので、ぜひこれを統計の勉強のきっかけにでもしてもらえればと思います。
解説を始める前に
この記事の対象読者
- ポケモンが好き
- 捕まえたポケモンの個体値はちゃんとチェックしている
- 統計解析をかじろうと思っている
- どうせなら楽しみながら勉強したい
- 「まずは実装、理論はその後」が許せる人
実験環境
使用言語
今回の解析は実はExcelでもできてしまうのですが、**せっかくなのでPythonでスクリプトを組んでみようかと思います。**Pythonのバージョンは3.5.0です。
開発環境はなんでも良いと思いますが、僕は主に普段使い慣れているSublime Text3とターミナルで作りました。
使用するデータ
今回は自宅周辺と東京神楽坂近辺で2016年の夏から秋頃に捕まえた、コイキングのデータ($n=100$)を使いました ![]()
データの取得は以下の方法で行います。
- ポケモンを捕まえる
- 名前に捕まえたおおよその地名を記入
- 個体値の確認画面でスクリーンショットを取る
- 博士に送る
- スクリーンショットを見てデータを手入力
いやーアナログな方法なのでけっこう大変でした(笑)
Google Photoや DropboxでコンピューターとSyncしておくと便利です、こんな感じで集まった画像から固有値を手入力していきます (Deep Learningで値を自動読み取りとかできたらなぁ...)
打ち込んだデータはCSV形式にして保存。
ぼくの集めたデータを使いたいという方はこちらから。
CSVデータの列構成は以下のようになっています。
- Place: 捕まえたおおよその場所ラベル、今回は自宅か神楽坂
- CP: CP
- Weight: 体重(kg)
- Weight EX: 体重でXSやXLがある場合はそのどちらかを記入
- Height: 身長(m)
- Height EX: 身長でXSやXLがある場合はそのどちらかを記入
今回の分析で使うのはこれらのうちCP, Weight, Heightの3列のみになります。
前提条件
本来は統計的手法で分析するにはいろいろな「前提条件」が必要となりますが、今回はその多くを無視して「とりあえずやってみる」的な感じで書いているのでご容赦ください。
- 前述で使用すると宣言した3列以外の変数や要因 (時間やプレイヤーレベル etc)は、体重や身長に一切影響していないという前提で進めます。本来はこういった要因も考慮しないといけないのですが、あくまで統計入門の記事にしたいので考察はせず進めることにします。
- また相関分析を行うには両変数の同時分布が2次元正規分布に従うという前提を満たしていなければなりません。体重と身長については経験的に見て「おそらく従っている」と判断しました。しかしCPでは経験的に見ておそらくこれを満たしていないため、そもそも相関分析の対象として不適切ですが、それを無視してあえて相関分析を行っています。
分析方法
ではいよいよ本題の分析に入ります。
まずはCSVデータを取り込んで一度散布図にplotしてみましょう ![]()
今回は読み込んだデータを、PythonのライブラリであるPandasを用いてdataframe型へ変換します。
from pandas.tools.plotting import scatter_matrix
import matplotlib.pyplot as plt
import pandas as pd
data = pd.read_csv("magikarp.csv")
print(data.describe())
plt.figure()
scatter_matrix(data)
plt.savefig("image.png")
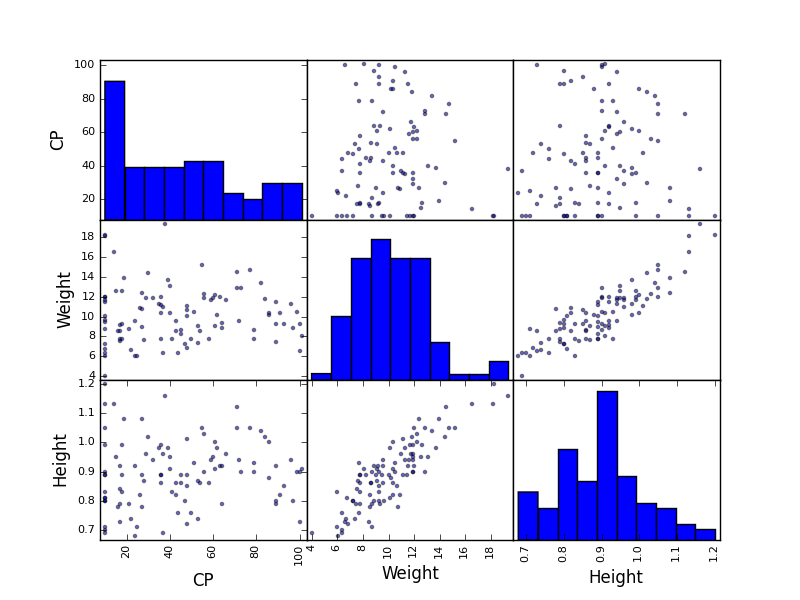
各変数の散布図はこのようになりました。
コイキングの場合、体重と身長はかなりキレイな直線的分布を見せていますね。
かなり小さいものから巨大なコイキングまで、現実の魚とほぼ同じようなリアリティで生態分布しているようです ![]()
一方で対CPについては、ちょっと分からない感じになっています...
ヒストグラムを見ると、CPが10のものが突出して多く、他の範囲のCPでは個体数に差がないように見えます。
ポケモンGOでは最低のCPが10であり、コイキングのような弱いポケモンでは特にCP10の個体の出現頻度が高いというのは、実際プレイしていて確かに感じますよね ![]()
では次に、これらの変数の相関係数($\alpha$)を求めます。
この値は変数間に直線的な関係性があるかどうかを表す指標で、絶対値が1に近いほど個体値間に強い直線的な関連性があるということを表します。
相関係数はdataframeのcorr関数を使います。
これによってdataframe内の全ての変数間で相関係を計算してくれるという素晴らしい関数です。
print(data.corr())
# > CP Weight Height
# > CP 1.000000 0.010724 0.086286
# > Weight 0.010724 1.000000 0.865564
# > Height 0.086286 0.865564 1.000000
先程のプロットを見て期待した通りの値になっていることが確認されました。
体重と身長の相関係数は0.866とかなり相関が強くなっているのがわかります。
一方CPの相関係数は見たところあまり大きくなく「相関がある」と言い切るにはちょっと説得力に欠けそうです。
よって最後にこれらの相関係数に有意性があるかを、無相関検定で確認します。
無相関検定では「得られた相関係数が0である」という仮説(帰無仮説)を設定し、それに対して「相関係数が偶然的に0である確率は極めて少ない」というような有意確率を得ることで、それが本当に意味のある相関係数なのかを確かめる手法です。
今回は
帰無仮説 $H_0: \alpha = 0$
対立仮説 $H_1: \alpha \neq 0$
として検定しています。
Scipyには「ピアソンの積率相関係数」(無相関検定には他にもいくつか種類がある)を使った検定を行うための関数pearsonrがあるので、これを各変数の組み合わせごとに実行して検定します。
2つの対応する変数を与えると、相関係数$r$と、有意確率$p$を返します。
from scipy.stats import pearsonr
...
r, p = pearsonr(data.Height, data.Weight) # 身長と体重
# r, p = pearsonr(data.Height, data.CP) # 身長とCP
# r, p = pearsonr(data.Weight, data.CP) # 体重とCP
print('相関係数 r = {r}'.format(r=r))
print('有意確率 p = {p}'.format(p=p))
print('有意確率 p > 0.05: {result}'.format(result=(p > 0.05)))
検定の結果はこちらのとおりとなりました。
今回は有意確率$p$が$0.05$を下回った場合(結果内True)には「$\alpha=0$で相関が無い」という$H_0$を採択し、そうでなければ$H_0$を棄却します。
> 相関係数 r: 0.8655637883468845
> 有意確率 p: 1.7019782502122307e-31
> 有意確率 p > 0.05: False # 有意
やはり予想通り有意な相関があることが証明されました。
> 相関係数 r: 0.0862864395740605
> 有意確率 p: 0.39090582918188466
> 有意確率 p > 0.05: True # 有意ではない
> 相関係数 r: 0.01072432286085844
> 有意確率 p: 0.915233564101408
> 有意確率 p > 0.05: True
一方CPについても最後まで期待通りの結果となりました。
CPと他の変数の相関を調べること自体に意義があるかどうかという問題の方が明らかにあるのですが、あくまで簡単な例では有りましたが、こうした方法でゲームの出現パラメータをある程度予測できるということがわかったのではないでしょうか。
まとめ
ということで超簡単ではありましたが、ポケモンのデータを使って相関分析的なことをしてみました。
今回のデータの分布はゲームのパラメータの分布なので、他のポケモンや、あるいは他のゲームでも記録をつけてパラメータを推定するみたいなことをするのは面白いかもしれません。
もしかしたらコイキング以外のポケモンではもっと個体値の分布が大きく異なるかもしれません。
今回無相関検定編としましたが、同じようなことを他にもやってみたいと思っているので、どこかで続きを書きたいと思います。
それまでにもっと統計の勉強もしておかないと...