前回の記事では相関がある $2$ つの擬似乱数を生成しました。しかし、色々やっていくうちにやっぱり相関がある乱数が $n$ 個ほしくなったので、その生成法を説明します。
今回はいきなり $n$ 個の乱数を作る話から入るので、前回の記事をまず読んでいただいたほうがスムーズかと思います。
追記:単に相関がある乱数を作りたい、バックグラウンドには興味ないという方は numpy.random.multivariate_normal を使えば大丈夫です。
概要
$n$ 個のデータ系列があったとき、 $i$ 番目と $j$ 番目の相関係数を $ij$ 成分においた対称行列を1、 相関行列 といいます。この相関行列をインプットとして、与えられた相関を満たすような $n$ 個の乱数を生成する方法を考えます。
平均がゼロで分散が等しい独立な乱数を $n$ 個用意して、それをベクトルでまとめて $X = (X_1 \ \ X_2 \ \ \dots \ \ X_n)^T$ と表現します2。このとき、$X_1$ や $X_2$ などと同じ分散を持っていて相関行列 $R$ で相関しあう $n$ 個の乱数 $Z = (Z_1 \ \ Z_2 \ \ \dots \ \ Z_n)^T$ は
Z = L \ X \tag{1}
で求められます。
ただし、相関行列は $Z_i$ と $Z_j$ の相関係数を $\rho_{ij}$ として
R = \left( \begin{array}{cccc}
\rho_{11} & \rho_{12} & \dots & \rho_{1n}
\\
\rho_{21} & & &
\\
\vdots & & \ddots & \vdots
\\
\rho_{n1} & & \dots & \rho_{nn}
\end{array} \right) \tag{2}
で、$L$ は $R$ のコレスキー分解から得られた下三角行列(対角成分より右上がすべてゼロの行列)です。
……はい、耳慣れない言葉がいっぱい出てきたかもしれませんが、一つひとつ解説していくので安心してください。笑
というわけでこの記事では、
- 理論:なぜこれで相関がある $n$ 個の乱数が作れるのか
- 検証:Python で実際にやってみる
について書いていきます。
コレスキー分解がどういうものかについても触れますが、実際にどうやって分解を実現するかは説明しませんのであしからず。
理論
理論の大まかな流れとしては、
- $\{Z_i\} = Z_1, Z_2, \dots, Z_n$ を $\{X_i\}$ を使って表現する方法を考える
- 得られた表現を、相関係数と関連付ける
- 表現を確定する
というような感じです。ではいってみましょう。
Z を作るアイディア
独立な乱数 $\{X_i\}$ について、平均はそれぞれゼロ、分散は同じ値で $\sigma^2$ とします。これらは独立なので、 共分散 $\mathrm{Cov}[X_i, X_j]$ や相関係数 $\mathrm{Corr}[X_i, X_j]$ はゼロです。
この $\{X_i\}$ を使って $\{Z_i\}$ を作っていきたいわけですが、とりあえず以下のようにしていきます。
\begin{align}
Z_1 &= a_{11} X_1 \tag{3.1}
\\
Z_2 &= a_{21} X_1 + a_{22} X_2 \tag{3.2}
\\
Z_3 &= a_{31} X_1 + a_{32} X_2 + a_{33} X_3 \tag{3.3}
\\
&\vdots
\\
Z_n &= a_{n1} X_1 + a_{n2} X_2 + \dots + a_{nn} X_n \tag{3.n}
\end{align}
これはまず基準となる $Z_1$ を作り、それに対して決められた相関をもつ $Z_2$ を作り、今度は $Z_1$ と $Z_2$ を基準としてそれぞれに対して決められた相関を持つ $Z_3$ を作り……ということを繰り返して $Z_n$ までいくイメージです。この部分を理解することは非常に重要です。なんなら理論パートの半分以上を占めると言っても過言ではないと思います。
ちょっとイメージをつかみやすくするために、$n = 3$ として考えてみてみましょう。イメージが完璧だ、という方はこの部分は読み飛ばしてください。
相関とは何かふたつのものの関係です。関係を考えるためには基準がないと始まらないので、
Z_1 = a_{11} X_1 \tag{4}
この部分は問題ないと思います3。次に、 $Z_1$ と他の乱数($X_2$ を選びましょう)を使って、
Z_2 = c Z_1 + a_{22} X_2 \tag{5}
とし、係数を適切に選ぶことで $Z_1$ と $\rho_{12}$ で相関する $Z_2$ が作れます。これも前回の記事を見ていただければ問題ないと思います。この式の右辺を $\{X_i\}$ だけにして
\begin{align}
Z_2 &= c_1 \cdot a_{11} X_1 + a_{22} X_2 & (\because Z_1 の式)
\\
&= a_{21} X_1 + a_{22} X_2 & (\because a_{21} = c_1 \cdot a_{11} とおいた) \tag{6}
\end{align}
これで2列目の式がでてきましたね。最後に $Z_3$ ですが、すでに乱数が2つあるため、以下のようにいろいろな場合が考えられます。
- 状況1. Z_2 より Z_1 とよく相関する
- 状況2. Z_1 より Z_2 とよく相関する
- 状況3. どちらとも相関しない
- 状況4. ……
これらの状況を幅広くカバーするためには、
Z_3 = c_1 Z_1 + c_2 Z_2 + a_{31} X_3
\tag{7}
と、$Z_1$、$Z_2$ と更に新たな乱数 $X_3$ の重ね合わせが必要となりそうですよね。実際、 $c_1$ を大きく取れば 状況1を、$c_2$ を大きくとれば 状況2を、$c_1 = c_2 = 0$ として $a_{31}$ だけを何かの数字にすれば状況3を表せそうです。この式の右辺をまた $\{X_i\}$ のみで表し、係数を適当に定義し直すことによって3列目の式も導けます。
このようにして、すでに作った $Z_1, Z_2, \dots, Z_i$ と新たな乱数 $X_{i + 1}$ を重ね合わせることによって $Z_{i + 1}$ が作れそうなことがわかりました。
相関係数と関連付ける
さて、先程の $\{Z_i\}$ を求める式を行列として表現してやると、
Z =
\left(
\begin{array}{ccccc}
a_{11} & 0 & 0 & \dots & 0
\\
a_{21} & a_{22} & 0 & \dots & 0
\\
a_{31} & a_{32} & a_{33} & & \vdots
\\
\vdots & \vdots & & \ddots & 0
\\
a_{n1} & a_{n2} & & \dots & a_{nn}
\end{array}
\right)X
\tag{8}
と書けます。これがまさしく先程ちらっと出てきた「下三角行列」で、対角成分とその左下には値が入っており、右上はすべてゼロで埋め尽くされているという行列ですね。
この行列が $Z = L \ X$ の中に出てきた $L$ に相当するわけです。そうとわかれば、あとは係数 $\{a_{ij}\}$ を、与えられた相関を満たすように決めてあげるだけです。つまり、$\{a_{ij}\}$ と $\{\rho_{ij}\}$ の関係がわかればいいわけです。
$Z_i$ と $Z_j$ の間の相関 $\rho_{ij}$ が与えられたとき、満たすべき式は
\mathrm{Corr}[Z_i, Z_j] = \rho_{ij}
\tag{9}
ですね。まんまですが。
このままだと何も言えないので、左辺を変形していきます。
LHS = \frac{\mathrm{Cov}[Z_i, Z_j]}{\sqrt{\mathrm{Var}[Z_i]} \sqrt{\mathrm{Var}[Z_j]}} \ (\because \mathrm{Corr} の定義)
\tag{10}
ここで、結果を先取りして $\mathrm{Var}[Z_k] = \sigma^2 \ (\mathrm{for \ all} \ k)$ を認めてしまいましょう。$\{Z_k\}$ の分散は $\{X_k\}$ の分散と同じになりますよということを仮定するのです(でないと計算がややこしくなるので)。これについては、あとで数値的に検証します。
というわけで、上の式は
\frac{\mathrm{Cov}[Z_i, Z_j]}{\sigma^2}
\tag{11}
となります。次は、分子を $\{X_i\}$ で展開していきます。$i \geq j$ として、
\begin{align}
\mathrm{Cov}[Z_i, Z_j] &= \mathrm{Cov}[a_{i1} X_1 + a_{i2} X_2 + \dots + a_{ii} X_i, \
a_{j1} X_1 + a_{j2} X_2 + \dots + a_{jj} X_j]
\tag{12}
\end{align}
ですが、$\mathrm{Cov}$ には
\mathrm{Cov}[a A + b B, c C + d D] = ac \mathrm{Cov}[A, C] + ad \mathrm{Cov}[A, D] + bc \mathrm{Cov}[B, C] + bd \mathrm{Cov}[B, D]
\tag{13}
という性質があるので(小文字は定数で大文字が乱数)、先程の式も同じように分解できます。さらに、今の場合 $\mathrm{Cov}[X_k, X_k] = \sigma^2$ 、$\mathrm{Cov}[X_k, X_l] = 0 \ (k \neq l)$ なので、
\begin{align}
\mathrm{Cov}[&a_{i1} X_1 + a_{i2} X_2 + \dots + a_{ii} X_i, \
a_{j1} X_1 + a_{j2} X_2 + \dots + a_{jj} X_j]
\\
&= a_{i1} a_{j1} \mathrm{Cov}[X_1, X_1] + a_{i2} a_{j2} \mathrm{Cov}[X_2, X_2] + \dots + a_{ij} a_{jj} \mathrm{Cov}[X_j, X_j]
\\
&\ \ \ \ + a_{i(j+1)} \cdot 0 \cdot \mathrm{Cov}[X_{j+1}, X_{j+1}] + \dots
\\
&= a_{i1} a_{j1} \sigma^2 + a_{i2} a_{j2} \sigma^2 + \dots + a_{ij} a_{jj} \sigma^2
\\
&= (a_{i1} a_{j1} + a_{i2} a_{j2} + \dots + a_{ij} a_{jj}) \ \sigma^2
\tag{14}
\end{align}
となります。$a_{j(j+1)} = a_{j(j+2)} = \dots = a_{ji} = 0$ なので、項は $j$ 番目で打ち切りになるのがミソですね。
最終的に、相関係数は
\rho_{ij} = \mathrm{Corr}[Z_i, Z_j] = a_{i1} a_{j1} + a_{i2} a_{j2} + \dots + a_{ij} a_{jj}
\tag{15}
と、こんな形になります。
$i \geq j$ を仮定して計算してきたので相関行列の下三角の部分を計算したことになるのですが、相関行列は必ず対称なので、
\rho_{ji} = a_{i1} a_{j1} + a_{i2} a_{j2} + \dots + a_{ij} a_{jj}
\tag{16}
も成り立ちます。左辺の添字がこっそり入れ替わってます。
行列を「解く」
これまでの議論を行列の形にまとめると、相関行列 $R$ は、$\{a_ij\}$ を使って
R = \left( \begin{array}{cccc}
a_{11} a_{11} & a_{21} a_{11} & \cdots & a_{n1} a_{11}
\\
a_{21} a_{11} & a_{21} a_{21} + a_{22} a_{22} &
\\
\\
\vdots & & \ddots & \vdots
\\
a_{n1} a_{11} & a_{n1} a_{21} + a_{n2} a_{22} & \dots &
\end{array} \right)
\tag{17}
と、こんなふうに表せます。$R$ には $\{\rho_{ij}\}$ を使った表現と $\{a_{ij}\}$ を使った表現の2通りがあるので、これでこのふたつを対応づけられたことになります。あとは、これを $\{a_{ij}\}$ について解けばいいわけですね。
確認のため、$n = 2$ で計算してみます。相関行列と係数の対応は
\left( \begin{array}{cc}
a_{11} a_{11} & a_{21} a_{11}
\\
a_{21} a_{11} & a_{21} a_{21} + a_{22} a_{22}
\end{array} \right)
=
\left( \begin{array}{cc}
\rho_{11} & \rho_{12}
\\
\rho_{21} & \rho_{22}
\end{array} \right)
\tag{18}
です。相関行列なので、$\rho_{11} = \rho_{22} = 1$ だし、$\rho_{21} = \rho_{12}$ ですね。
これを踏まえて意味のある式を抜き出すと、
\begin{align}
a_{11}^2 &= 1
\tag{19.1}
\\
a_{21} a_{11} &= \rho_{21}
\tag{19.2}
\\
a_{21}^2 + a_{22}^2 &= 1
\tag{19.3}
\end{align}
と、この3本です。ここで、$a_{kk} > 0 \ (\mathrm{for \ all} \ k)$ としておきましょう。これを解くと、
\begin{align}
a_{11} &= 1
\tag{20.1}
\\
a_{21} &= \rho_{21}
\tag{20.2}
\\
a_{22} &= \sqrt{1 - \rho_{21}^2}
\tag{20.3}
\end{align}
となり、前回求めた結果と一致していますね。よさそうです。
ではもっと一般的に $n$ 次元の行列のときはどうといたらいいでしょうか? もう一度行列をよく見てみましょう。もうちょっと書く成分を増やしてみました。
R = \left( \begin{array}{ccccc}
a_{11} a_{11} & a_{21} a_{11} & a_{31} a_{11} & \cdots & a_{n1} a_{11}
\\
a_{21} a_{11} & a_{21} a_{21} + a_{22} a_{22} &
a_{31} a_{21} + a_{32} a_{22} &
\\
a_{31} a_{11} & a_{31} a_{21} + a_{32} a_{22} & a_{31} a_{31} + a_{32} a_{32} + a_{33} a_{33}
\\
\vdots & \vdots & & \ddots & \vdots
\\
a_{n1} a_{11} & a_{n1} a_{21} + a_{n2} a_{22} & \dots &
\end{array} \right)
\tag{21}
結構キレイな形をしていますよね。実はこれ、
R = \left(
\begin{array}{ccccc}
a_{11} & 0 & 0 & \dots & 0
\\
a_{21} & a_{22} & 0 & \dots & 0
\\
a_{31} & a_{32} & a_{33} & & \vdots
\\
\vdots & \vdots & & \ddots & 0
\\
a_{n1} & a_{n2} & & \dots & a_{nn}
\end{array}
\right)
\left(
\begin{array}{ccccc}
a_{11} & a_{21} & a_{31} & \dots & a_{n1}
\\
0 & a_{22} & a_{32} & \dots & a_{n2}
\\
0 & 0 & a_{33} & &
\\
\vdots & \vdots & & \ddots & \vdots
\\
0 & 0 & & \dots & a_{nn}
\end{array}
\right)
\tag{22}
という形に分解できると言ったら驚くでしょうか? 実際これは本当で、このあたりが数学の美しいところですよね。
$n = 3$ として確認してみましょう。手計算はしんどいので、ここは SymPy を使います。SymPy は、Mathematica のような数式の計算をしてくれる Python のライブラリです。
試しに分解された行列を掛けてもとに戻るか見てみましょう。
import sympy
# Define symbols
a_11, a_22, a_33 = sympy.symbols('a_11 a_22 a_33', real=True, positive=True)
a_21, a_31, a_32 = sympy.symbols('a_21 a_31 a_32', real=True)
# Define lower and upper triangular matrices
L = sympy.Matrix([
[a_11, 0, 0],
[a_21, a_22, 0],
[a_31, a_32, a_33]
])
U = L.transpose()
# Calculate product of triangular matrices
R = L * U
print("R = {}".format(R))
出力はこちら。見やすいように整形してます4。
R = Matrix([
[a_11**2, a_11 * a_21, a_11 * a_31 ],
[a_11 * a_21, a_21**2 + a_22**2, a_21 * a_31 + a_22 * a_32 ],
[a_11 * a_31, a_21 * a_31 + a_22 * a_32, a_31**2 + a_32**2 + a_33**2]
])
なんと! きちんと期待された結果が出てきていますね!
逆に言うと、「ある行列を下三角行列とその転置(上三角行列)の積に分解する」という操作こそがコレスキー分解なのです。せっかくなのでこれもやってみましょう。
import sympy
# Define symbols
a_11, a_22, a_33 = sympy.symbols('a_11 a_22 a_33', real=True, positive=True)
a_21, a_31, a_32 = sympy.symbols('a_21 a_31 a_32', real=True)
# Define correlation matrix
R = sympy.Matrix([
[a_11**2, a_11 * a_21, a_11 * a_31 ],
[a_11 * a_21, a_21**2 + a_22**2, a_21 * a_31 + a_22 * a_32 ],
[a_11 * a_31, a_21 * a_31 + a_22 * a_32, a_31**2 + a_32**2 + a_33**2]
])
# Perform cholesky decomposition
L = R.cholesky()
print("L = {}".format(L))
出力。
L = Matrix([
[a_11, 0, 0 ],
[a_21, a_22, 0 ],
[a_31, a_32, a_33]
])
うおお、きちんとなっている! コレスキー分解でキレイに係数が取り出せていますね!
これで、相関係数 $R$ をコレスキー分解したものが、相関のある乱数を生成してくれる行列であることが確認できました!
理論のまとめ
長くなってきたので、ここで一旦まとめます。
相関のある $n$ 個の乱数の作り方:
- 相関行列 $R$ を用意する。
- $R$ をコレスキー分解して下三角行列 $L$ を求める。
- $L$ を相関がない乱数の列ベクトル $X$ に左から掛ければできあがり!
概要と言ってることがまったく変わってないですが、だいぶイメージはつかめたはずです。
繰り返しますが、コレスキー分解をどのように計算するか、ということはここでは触れません。ただ単に、行列を三角行列に分解するブラックボックスとして扱います。計算法については調べればいろいろと出てくるので、そちらをどうぞ。
検証
長かったですが、いよいよ Python3 で検証です。前回の反省を踏まえ、最初から正規乱数でいきます。
import numpy as np
import numpy.random as rand
import matplotlib.pyplot as plt
# Set parameters
n = 3 # The number of random numbers
size = int(1e4) # Size of the vector
r_in = np.matrix([
[1, 0.2, 0.8],
[0.2, 1, 0.6],
[0.8, 0.6, 1]
]) # Correlation matrix
# Generate correlated random numbers
l = np.linalg.cholesky(r_in)
x = rand.randn(n, size)
z = l * x
# Calculate stats
cov = np.cov(z)
r_out = np.corrcoef(z)
print("covariance matrix:\n{}\n".format(cov))
print("correlation matrix:\n{}\n".format(r_out))
# Plot results
fig, ax = plt.subplots()
ax.scatter(z[0, :], z[1, :], s=1, color='red', label='Z_2')
ax.scatter(z[0, :], z[2, :], s=1, color='blue', label='Z_3')
ax.set_xlabel('Z_1')
ax.set_ylabel('Z_2, Z_3')
ax.legend()
plt.show()
出力はこれ。
covariance matrix:
[[ 1.00545504 0.19297604 0.79517079]
[ 0.19297604 1.00391907 0.5943957 ]
[ 0.79517079 0.5943957 0.99000159]]
correlation matrix:
[[ 1. 0.19207582 0.79700517]
[ 0.19207582 1. 0.5962225 ]
[ 0.79700517 0.5962225 1. ]]
Covariance matrix(共分散行列)の対角成分は分散です。もとの正規乱数と同じ、分散 $1$ に近い値が出ているので、理論のところでおいた、「$\{Z_i\}$ の分散は $\{X_i\}$ と等しい」という仮定は問題なさそうですね。
また、Correlation matrix(相関行列)のほうでは、きちんとインプットした値に近い数字が出てきています。
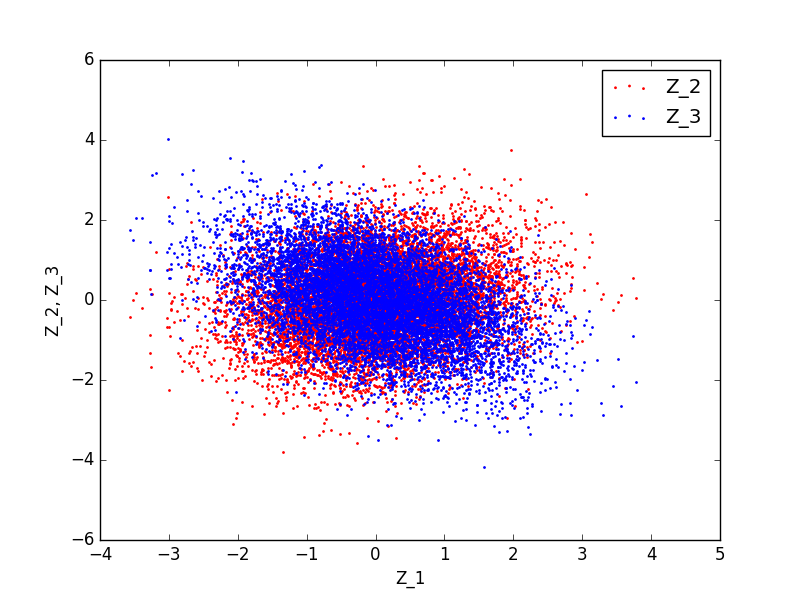
$Z_1$ に対する $Z_2$ と $Z_3$ のプロットはこちら。
$\rho_{13}$ に強めの相関を入れたのがきちんと反映されていますね!
ではこんな相関行列はどうでしょう? 負の相関も見たいですよね。
r_in = np.matrix([
[1, -0.2, -0.8],
[-0.2, 1, -0.6],
[-0.8, -0.6, 1]
]) # Correlation matrix
実行すると……
Traceback (most recent call last):
File "spike.py", line 15, in <module>
l = np.linalg.cholesky(r_in)
File "/Users/horiem/.pyenv/versions/anaconda3-4.0.0/lib/python3.5/site-packages/numpy/linalg/linalg.py", line 612, in cholesky
r = gufunc(a, signature=signature, extobj=extobj)
File "/Users/horiem/.pyenv/versions/anaconda3-4.0.0/lib/python3.5/site-packages/numpy/linalg/linalg.py", line 93, in _raise_linalgerror_nonposdef
raise LinAlgError("Matrix is not positive definite")
numpy.linalg.linalg.LinAlgError: Matrix is not positive definite
shell returned 1
おっとエラーが出ましたね(そして pyenv と anaconda を使ってることがバレてしまいましたね)。どうやらコレスキー分解に失敗しているようです。"Matrix is not positive definite" と怒っていますね。
そうです、実は、コレスキー分解ができるためには、対象となる行列が:
- 対称行列である(複素数の場合はエルミート)
- 正定値行列(positive definite)である
ことが必要なんです。
正定値行列って何じゃっていうと、任意の非ゼロベクトル $\boldsymbol{z}$ に対して、
\boldsymbol{z}^T M \boldsymbol{z} > 0
となるような対称行列 $M$ のことです5。
そんなのいちいち確認してられないよっていう人のために、いい方法があります。「行列 $M$ が正定値であること」と「行列 $M$ の固有値がすべて正であること」は同値です。なので、固有値の符号を調べてみましょう。
r_in = np.matrix([
[1, -0.2, -0.8],
[-0.2, 1, -0.6],
[-0.8, -0.6, 1]
]) # Correlation matrix
w, v = np.linalg.eig(r_in)
print(w)
[-0.10192577 1.19135241 1.91057336]
あちゃ〜、やっぱり負の固有値がありますね。これじゃあコレスキー分解できません。
えーじゃあ負の相関があるときはコレスキー分解できないってこと? いやいや、そうではありません。
実は、どんな相関行列にももともと非負定値性(半正定値性)があります。非負定値性は、さっきの正定値性の条件にゼロを含んだ場合です。つまり、固有値がゼロか正になるってことですね。固有値がゼロのものを含む例としては、
\left( \begin{array}{ccc}
1 & 1 & -1
\\
1 & 1 & -1
\\
-1 & -1 & 1
\end{array} \right)
とかですね。これは非負定値なので相関行列の資格はありますが、正定値ではないのでコレスキー分解できないというレアケースです(でも、必要ないよね??)。
さらに、こんな行列
\left( \begin{array}{ccc}
1 & -1 & -1
\\
-1 & 1 & -1
\\
-1 & -1 & 1
\end{array} \right)
これも一見相関行列っぽいですが非負定値ですらないので相関行列の資格がありません。考えてみれば明らかで、$Z_1$ と $Z_2$ が逆相関、$Z_2$ と $Z_3$ も逆相関、$Z_3$ と $Z_1$ も逆相関なんてありえませんよね? これの言っていることは
\begin{align}
Z_1 = - c_2 Z_2
\\
Z_2 = - c_3 Z_3
\\
Z_3 = -c_1 Z_1
\end{align}
ということです($c_1, c_2, c_3 > 0$)。これを全部代入していくと $Z_1 = (負の定数) \times Z_1$ となって、矛盾が起きます。こういう正しくないデータは数学のシステムのほうで弾いてくれているんですね。すごい。
先程エラーが出た例も、パッと見相関行列っぽいものでしたが、負の固有値が含まれていたので非負定値でありません。つまり、実際には相関行列とは呼べないチンプンカンプンのデータだったってことですね。
なので、負の相関を入れるときはもうちょっとマイルドにしてあげなければいけません。例えば
r_in = np.matrix([
[1, 0.2, -0.4],
[0.2, 1, 0.6],
[-0.4, 0.6, 1]
]) # Correlation matrix
こんな感じですね。一応固有値をチェックすると……
[ 0.17738188 1.18223576 1.64038236]
全部正。よかった。回してみると……
covariance matrix:
[[ 1.0117086 0.17839112 -0.42687826]
[ 0.17839112 0.98871838 0.60641387]
[-0.42687826 0.60641387 1.03022947]]
correlation matrix:
[[ 1. 0.17836482 -0.41812808]
[ 0.17836482 1. 0.60084968]
[-0.41812808 0.60084968 1. ]]
いい感じに逆相関が出ています! やったね!
まとめ
相関がある $n$ 個の乱数がどのように作れるか? そして、それはなぜか? を見てきました。こういうネタでは必ず「コレスキー分解をせよ」と言われるのですが、なぜそれでうまくいくのかまで言及している記事はあまりないんじゃないでしょうか。計算自体も、項が多くて(書くのが)ちょっとめんどくさいですが、線形代数と統計の基礎的な部分だけで十分最後までいけます。やはり、$n$ 個の変数を扱い始めたら必ず線形代数が顔を出しますね。
検証の方では、相関行列っぽく見えても実は相関行列とは呼べないようなものもいることがわかりました。各成分が $-1$ から $1$ の間ってだけじゃダメなんですね。
いろいろ手を動かしてみるといろいろな発見があって楽しいです。相関のある乱数生成は手を動かすにはちょうどいいネタだと思うので、みなさんもぜひ統計学を楽しんでみてください!
-
つねに $( \ i \ と \ j \ の相関) = ( \ j \ と \ i \ の相関)$ であるため。 ↩
-
$X$ は成分が縦に並んだ「列ベクトル」ですが、紙面がもったいないので行ベクトルの転置として表現しています。 ↩
-
$\{X_i\}$ と $\{Z_i\}$ は同じ分散を持つとしてるので $a_11 = 1$ がただちにわかるのですが、ここは記号のままにしておきます。 ↩
-
インタラクティブモードでやると行列っぽく出てくるのですがあんまり見やすくないのでスクリプトでやってます。 ↩
-
なので実際にはコレスキー分解ができるための条件は、「対称の行列が正定値であること」で十分です。 ↩