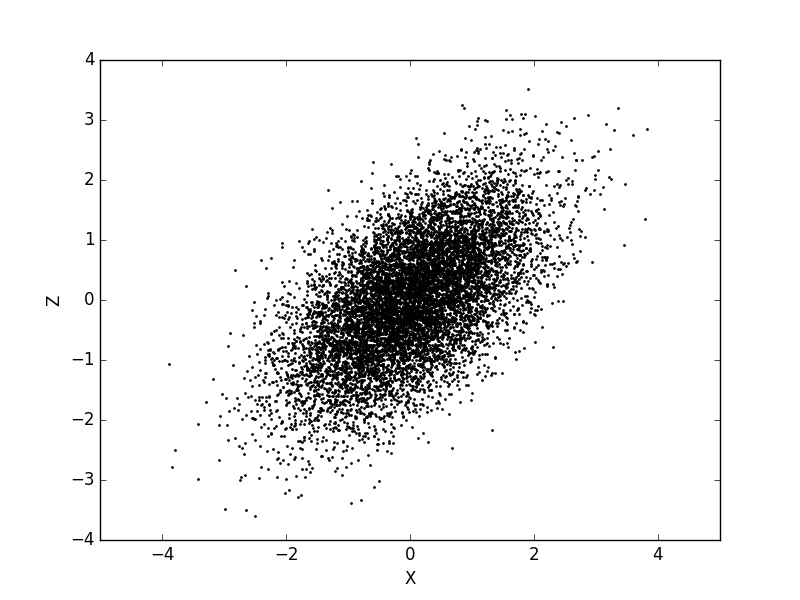
統計的な数値実験をしているときに、相関のある乱数を生成したいことがあります。ちょっと検索するとコレスキー分解を使った方法が出てきます。これはこれで変数の数がいくつでも対応できるやり方なのですが、僕が欲しかったのは $2$ 変数だけだったので、ここではもうちょっと泥臭いやりかたで説明します1。
概要
平均がゼロで分散が等しい独立な乱数 $X$ と $Y$ があるとします。このとき、$X$ と相関係数 $\rho$ で相関し、同じ分散を持つ乱数 $Z$ は
Z = \rho X + \sqrt{1 - \rho^2} Y
のように作れます。
この記事では、
- 理論:なぜこれで相関がある乱数が作れるのか
- 検証:Python で実際にやってみる
について書いていきます。
理論
独立な乱数 $X$ と $Y$ について、平均はそれぞれゼロ、分散は同じ値で $\sigma^2$ とします。$X$ と $Y$ は独立なので、共分散や相関係数はゼロです。
また、$X$ と相関を持たせたい乱数 $Z$ をとりあえず $X$ と $Y$ の重ね合わせで
Z = a X + b Y
と定義しておきます。$a$ と $b$ は定数です。
なぜこうしておくかというと、以下の極端な例に対して次のことが成り立つからです。
| $a$ | $b$ | $\rho$ |
|---|---|---|
| $> 0$ | $0$ | $1$ |
| $=0$ | $\neq 0$ | $0$ |
| $< 0$ | $0$ | $-1$ |
この表を見ると、$a$ と $b$ のバランスをうまく変えてやることで自由な相関係数が作れそうな予感がします2。なので、先程の $Z$ の表現は $X$ と任意の相関を持つ乱数として有望なわけですね。
では実際に $X$ と $Z$ の相関係数 $\rho$ を計算してみましょう。相関係数は
\rho = \frac{\mathrm{Cov}[X, Z]}{\sqrt{\mathrm{Var}[X]} \sqrt{\mathrm{Var}[Z]}}
で計算できます。ここで、$\mathrm{Cov}$、$\mathrm{Var}$ はそれぞれ共分散、分散です。まず手始めに共分散から計算してみましょう。
\begin{align}
\mathrm{Cov}[X, Z] &= \mathrm{Cov}[X, a X + b Y] & (\because Z \ の定義)
\\
&= a \ \mathrm{Cov}[X, X] + b \ \mathrm{Cov}[X, Y] & (\because \mathrm{Cov} \ の性質)
\\
&= a \ \sigma^2 & (\because \mathrm{Cov}[X, X] = \mathrm{Var}[X] = \sigma^2, \mathrm{Cov}[X, Y] = 0)
\end{align}
混乱しそうになる計算ですが、わからなくなったら定義に立ち返って落ち着いて計算すればたどり着けるはずです。もし面倒でしたら計算は追わなくても問題ないでしょう。
また、$Z$ の分散については、
\begin{align}
\mathrm{Var}[Z] &= \mathrm{Var}[a X + b Y] & (\because Z \ の定義)
\\
&= a^2 \mathrm{Var}[X] + b^2 \mathrm{Var}[Y] & (\because \mathrm{Var} \ の性質)
\\
&= a^2 \sigma^2 + b^2 \sigma^2 &
\end{align}
となりますから、計算したかった相関係数は、
\begin{align}
\rho &= \frac{\mathrm{Cov}[X, Z]}{\sqrt{\mathrm{Var}[X]} \sqrt{\mathrm{Var}[Z]}}
\\
&= \frac{a \ \sigma^2}{\sqrt{\sigma^2} \sqrt{a^2 \sigma^2 + b^2 \sigma^2}}
\\
&= \frac{a}{\sqrt{a^2 + b^2}}
\end{align}
と、なかなかきれいな式にまとまりました。この式を $b$ について解くと、
b = \frac{\sqrt{1 - \rho^2}}{\rho} a
が得られます。式をキレイにするためだけに $a = c \rho$ ($c$ は正の定数)と置くと、
Z = c \left( \rho X + \sqrt{1 - \rho^2} Y \right)
が得られます。この $c$ は $Z$ の分散をコントロールするためのパラメータで、実際、
\begin{align}
\mathrm{Var}[Z] &= \mathrm{Var}\left[{c \left( \rho X + \sqrt{1 - \rho^2} Y \right)} \right]
\\
&= c^2 \left[ \rho^2 \sigma^2 + (1 - \rho) \sigma^2 \right]
\\
&= c^2 \sigma^2
\end{align}
と、分散を $c^2$ 倍する(つまり標準偏差を $c$ 倍する)効果を持っています。これを $1$ とすることで冒頭の式
Z = \rho X + \sqrt{1 - \rho^2} Y
が得られるわけですね。
検証
では実際にPython3を使って得られた乱数が望みどおりのものか検証してみます。ひとまず $X$ と $Y$ には一様乱数を使ってみます。
import numpy as np
import numpy.random as rand
import matplotlib.pyplot as plt
size = int(1e3) # Size of the vector
rho_in = 0.6 # Correlation coefficient between two random variables
# Generate uniform random numbers with mean = 0
x = rand.rand(size) - 0.5
y = rand.rand(size) - 0.5
# Generate random numbers correlated with x
z = rho_in * x + (1 - rho_in ** 2) ** 0.5 * y
# Calculate stats
variance = np.var(z)
rho_out = np.corrcoef(x, z)[1][0]
print("variance: {}, correlation: {}".format(variance, rho_out))
# Plot results
fig, ax = plt.subplots()
ax.scatter(x, z, s=1)
ax.set_xlabel('X')
ax.set_ylabel('Z')
plt.show()
結果はこんな感じ。
variance: 0.08332907524577293, correlation: 0.5952102586280674
おや? 分散の値が中途半端ですね。相関係数のほうは狙い($0.6$)に近い値が出ているようですが。。
それもそのはず。生成される $Z$ の分散は $X$ の分散と同じなのでした。今 $X$ は区間$[-0.5, 0.5]$ の一様乱数で、その分散は 1 / 12 になるので、$1 / 12 = 0.0833...$ に近い値が出てきているのです。
結果の $Z$ - $X$ プロットはこんな感じ。一様乱数に一様乱数を足しているので、平行四辺形みたいな形をしていますね。
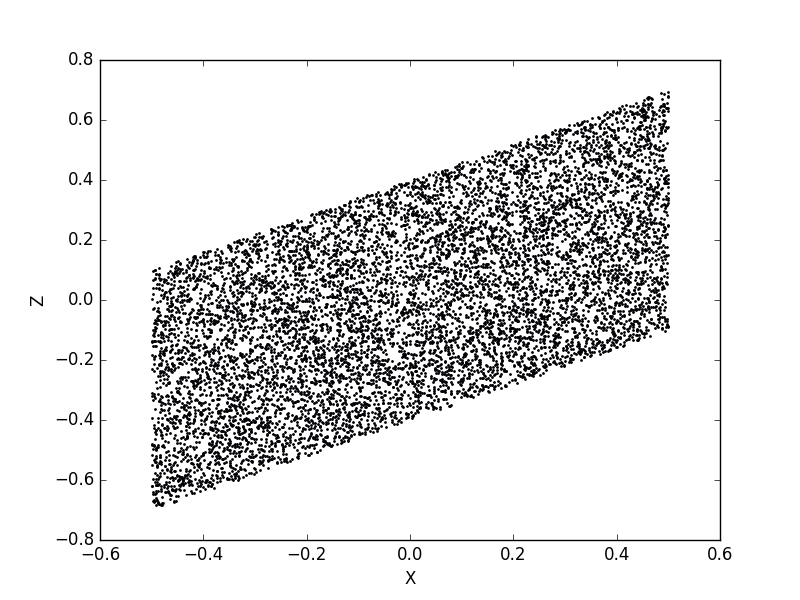
これがイヤな場合は、y のところを
y = rand.randn(size) * (1 / 12) ** 0.5
のように正規乱数に変えてやればよいです。$X$ と $Y$ で分散をそろえるため、一様乱数の標準偏差をかけています。
出力は以下。
variance: 0.0823649369923887, correlation: 0.5983078612793685
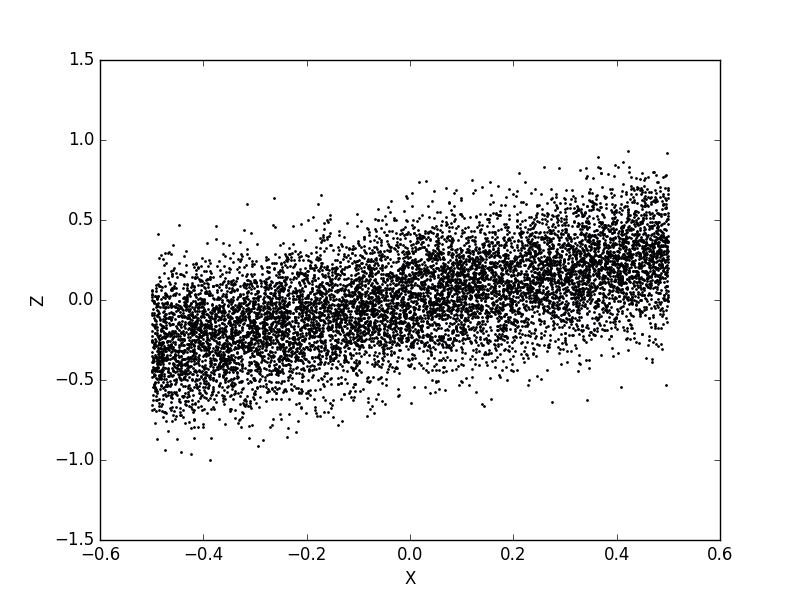
これはけっこういい感じに見えるので、僕はこれを使いました。
ただ、ひとつ注意があって、これらふたつの方法で作った乱数 $Z$ は一様乱数ではありません。$X$ も $Y$ も一様乱数を使った場合、ヒストグラムは以下のような台形みたいな形になります。
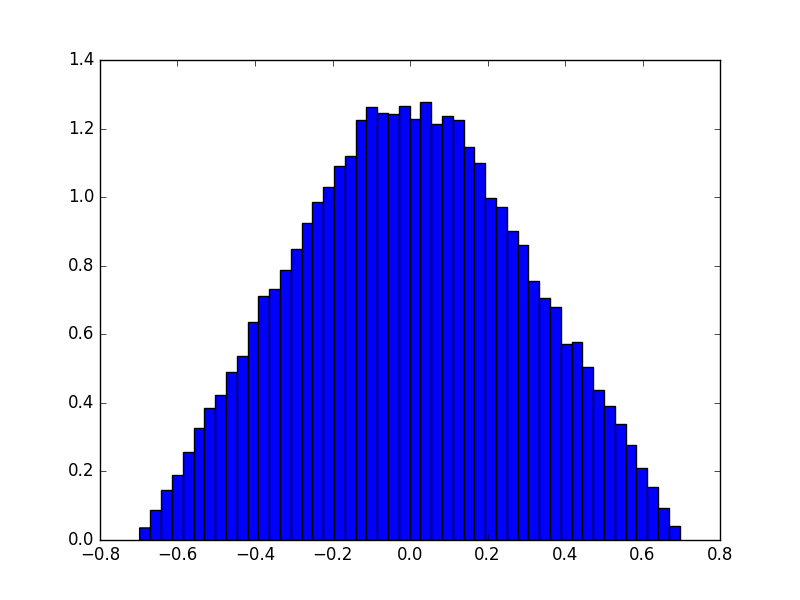
これは $Y$ に正規乱数を使ったときも同じで、山のカドがちょっと丸くなる感じになります。
これは、異なる一様分布にそれぞれ従う2つの確率変数を足しても一様分布になるとは限らないからで(まんまですね)、これを統計学の言葉で「再生性がない」と言います。なので、これを無理やりまた一様乱数に戻そうという試みもあります。
再生性があるのはどんな分布かというと、例えばみんな大好き正規分布とかですね。なので $X$ も $Y$ も正規乱数にしちゃえばいいじゃん! っていうのが以下のバージョンです。まあ、変わってるのは上の方の x と y のところだけです。
import numpy as np
import numpy.random as rand
import matplotlib.pyplot as plt
size = int(1e4) # Size of the vector
rho_in = 0.6 # Correlation coefficient between two random variables
# Generate normal random numbers
x = rand.randn(size)
y = rand.randn(size)
# Generate random numbers correlated with x
z = rho_in * x + (1 - rho_in ** 2) ** 0.5 * y
# Calculate stats
variance = np.var(z)
rho_out = np.corrcoef(x, z)[1][0]
print("variance: {}, correlation: {}".format(variance, rho_out))
# Plot results
fig, ax = plt.subplots()
ax.scatter(x, z, s=1)
ax.set_xlabel('X')
ax.set_ylabel('Z')
plt.show()
出力はこう。
variance: 0.9884508169450733, correlation: 0.5936089719053868
分散 $1$ の正規乱数を使って相関 $0.6$ を出そうとしたので、なかなか近い値が出てますね! もちろん相関係数は $[-1, 1]$ の範囲内だったら負とか、$1$ とかでも大丈夫です3。
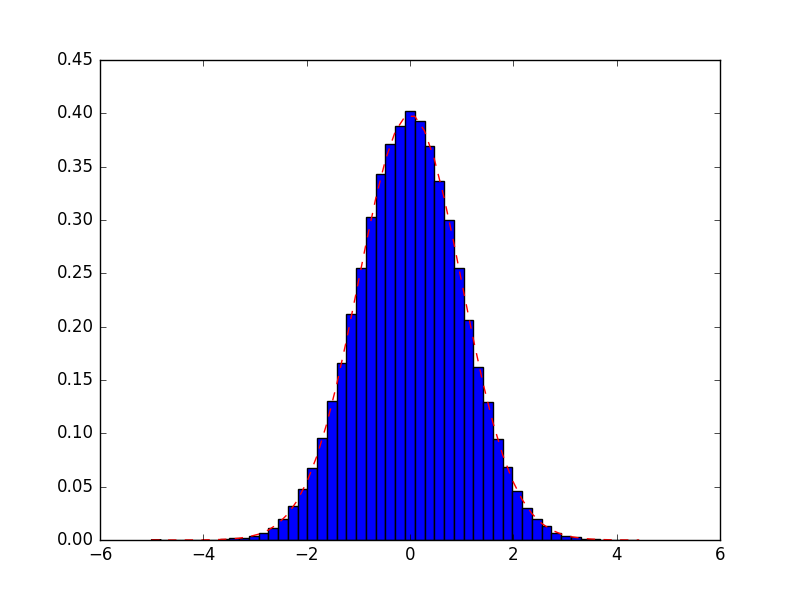
一応ヒストグラムも貼っておきます。赤い点線は理論的に予測される、平均ゼロで分散 $1$ の正規分布です。いい感じに一致してそうですね!
まとめ
相関がある乱数はどのように作れるか? そして、それはなぜか? を見てきました。慣れていない人は戸惑うかもしれませんが、分散の性質とかからゴリゴリ新しい乱数の分散を求めるという計算もやってみて損はないと思います(見た目以上にあっさりした計算なので)。これから統計学を学びたいと思っている方は、この記事の計算を追ってみるといいかもしれません。
また、一様乱数を単純に組み合わせただけではヘンテコな形の分布になってしまうことがわかりました。僕はあまり分布の形を気にしない軽い実験のためだったので $X$: 一様乱数、$Y$: 正規乱数のバージョンを使いましたが、分布まで気にする人は正規乱数を使うのがやはり手っ取り早いかもしれないですね。
あわせて読みたい
相関のある n 個の擬似乱数の生成(Python サンプルつき) - Qiita
続編です。$n$ 個の乱数がどのようにして作れるか? という解説をしています。