週刊少年ジャンプの短命作品を，機械学習で予測する （後編：学習と評価）

1. はじめに

本記事は，週刊少年ジャンプの短命作品を，機械学習で予測する （前編：データ分析）の続きです．前編で取得したデータを用い，多層パーセプトロンで分類器を実装・評価します．以降，ジャンプとは週刊少年ジャンプを指します．

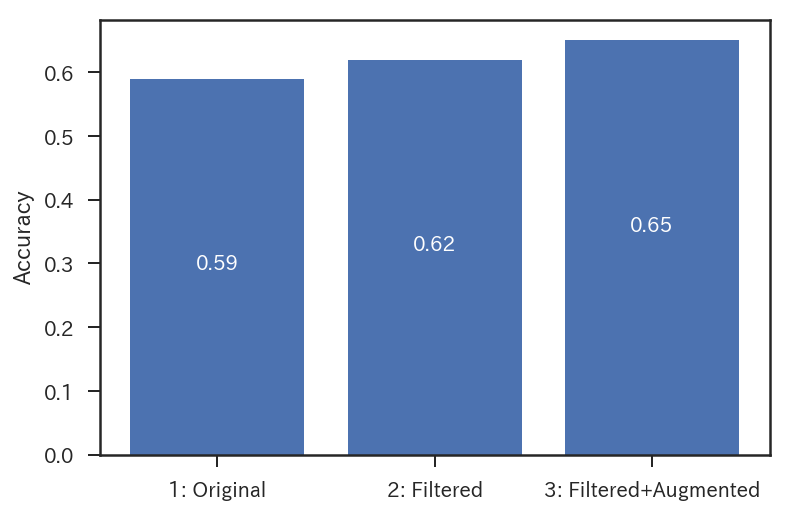
上図は，評価結果の一部です．最も優れたモデル（Filtered + Augmented）を用いた場合，7週目までの掲載順¹およびカラー回数を入力としたとき，65%の確率で20週以内に終了する作品を予測可能²なことがわかりました．評価には文化庁メディア芸術データベースに登録されている最新100作品を，学習およびパラメータ調整にはそれ以外の作品を用いました．色々工夫したのですが，私の力ではこの性能が限界でした．以下では，詳細をご説明します．jupyter notebookはこちら，ソースコードはこちらです．

なお，本記事はジャンプの編集方針についての意見を述べるものではなく，いかなる作品の終了・継続の不当性を訴えるものではありません．頑張れジャンプ！頑張れマンガ家さん！

2. 環境構築

2.1 anaconda

anacondaで，以下のような仮想環境comicを作成します．

conda create -n comic python=3.5
source activate comic
conda install pandas matplotlib jupyter notebook scipy scikit-learn seaborn scrapy
pip install tensorflow

ymlファイルはこちらです．tensorflowやscikit-learnを入れてあります．また，前編でpairplot()を使ったので，seabornを入れました．

2.2 目次情報

前編で取得したwj-api.jsonがdataディレクトリにあることを想定します．また，前編でご紹介したComicAnalyzerがcomic.pyで定義されていることを想定します．

import comic

wj = comic.ComicAnalyzer()

2.3 モジュール

日本語で漫画のタイトルを表示したいので，matplotlibで日本語を描画 on Ubuntuを参考に設定します．Ubuntu以外をお使いの方は，適宜ご対応ください．

import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf

import matplotlib
from matplotlib.font_manager import FontProperties
font_path = '/usr/share/fonts/truetype/takao-gothic/TakaoPGothic.ttf'
font_prop = FontProperties(fname=font_path)
matplotlib.rcParams['font.family'] = font_prop.get_name()

　

3. モデル

3.1 問題設定

本記事では，以下の入力をもとに，短命作品か否かを分類する問題に挑戦します．

入力

入力として，連載開始7週目までの各週掲載順と合計カラー回数の，計8次元の情報を用います．7週目までのデータを用いるのは，近年の最短連載（8週間）の，遅くとも一週間前に打ち切りを予測したいと考えたためです．掲載順だけでなくカラー回数を用いるのは，予測精度を上げるためです．直感的には，人気作品ほど，カラー回数が多い傾向があります．

短命作品

前編では，「短命作品」を以下のように定義しました．

本記事では，機械学習を使って，短命作品（10週以内に終了する作品）の予測を行います．

事前実験として，この定義で短命作品の分類に挑戦したのですが，うまく学習しませんでした．改めてwj-api.jsonを分析すると，10週以内に終了する作品が極めて少ないことがわかります．

左図は全作品の累積分布であり，右図は左図の50週までに注目したものです．横軸は掲載期間，縦軸は割合です．右図から，10週までに終了した作品は10%以下であることがわかります．なぜニューラルネットはSVMに勝てないのかでもご指摘のように，多層パーセプトロンはアンバランスなデータの学習が得意ではありません³．

Applying deep learning to real-world problems - Merantixによると，データラベルに偏りがある場合の対処法の一つとして，ラベリングの変更が提案されています．そこで本記事では，便宜上，短命作品の定義を20週以内に終了した作品に変更します（10週以内に終了した作品の予測については，今後の宿題とさせてください…）．閾値を20週にすると，約半数の作品を短命作品として扱えます．

3.2 多層パーセプトロン

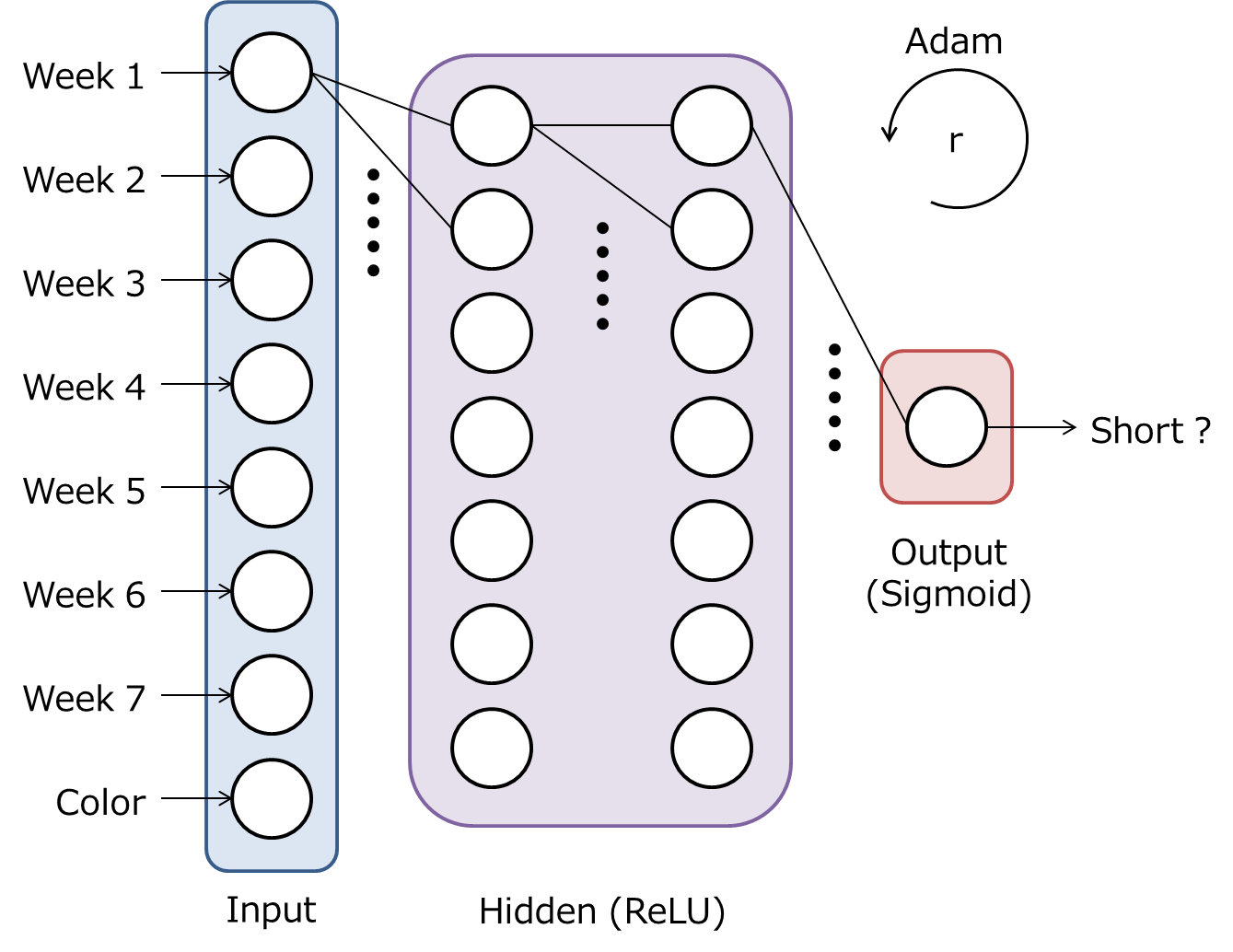
以下は，本記事で扱う多層パーセプトロンのモデルです．多層パーセプトロンついては，誤差逆伝播法のノートが詳しいです．

隠れ層は7ノード2層です．隠れ層の活性化関数として，ReLUを使います．出力層は短命作品である確率を出力し，活性化関数としてSigmoidを使います．学習には，Adamを使います．学習率$r$は，TensorBoardで調整します．ちなみに，上記のモデル（隠れ層の層数，隠れ層のノード数，隠れ層の活性化関数，最適化アルゴリズム）は，事前実験で最も性能が良かったものを選択しています．

3.3 データセット

本記事では，短命作品273作品，それ以外の作品（以下，継続作品）273作品の合計546作品を用います．新しい作品から順に100作品をtestデータ，100作品をvalidationデータ，346作品をtrainingデータとして用います．testデータは最終評価のためのデータ，validationデータはハイパーパラメータ調整のためのデータ，trainingデータは学習のためのデータです．これらについては，なぜ教師あり学習でバリデーションセットとテストセットを分ける必要があるのか？が詳しいです．

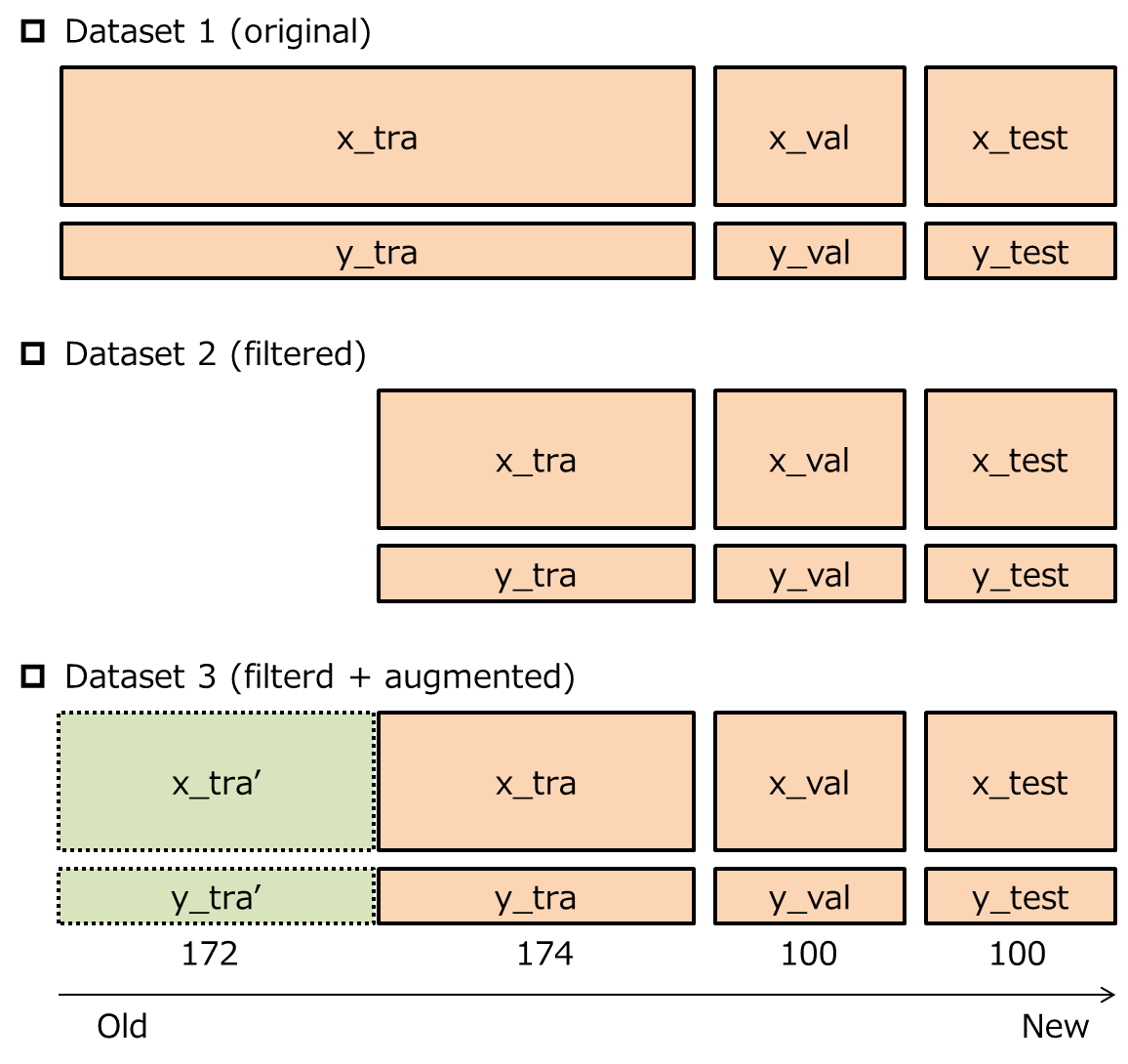
本記事では，以下３種類の異なる方法で，trainingデータを利用します．x_testおよびy_testはtestデータ，x_valおよびy_valはvalidationデータ，x_traおよびy_traはtrainingデータを表します．

Dataset 1では，trainingデータ346作品を全て学習に利用します．Dataset 2では，trainingデータのうち約半分の古い作品を除外して，学習に利用します．これは，trainingデータの一部の作品は古すぎて，現在のジャンプ編集部の打ち切り方針の学習に適さない（ノイズとなる）と考えたためです．Dataset 3では，Dataset 2をdataset augmentationにより水増しし，学習に利用します．これは，Dataset 2では学習データが少なすぎて，十分な汎化性能が得られないと考えたためです．

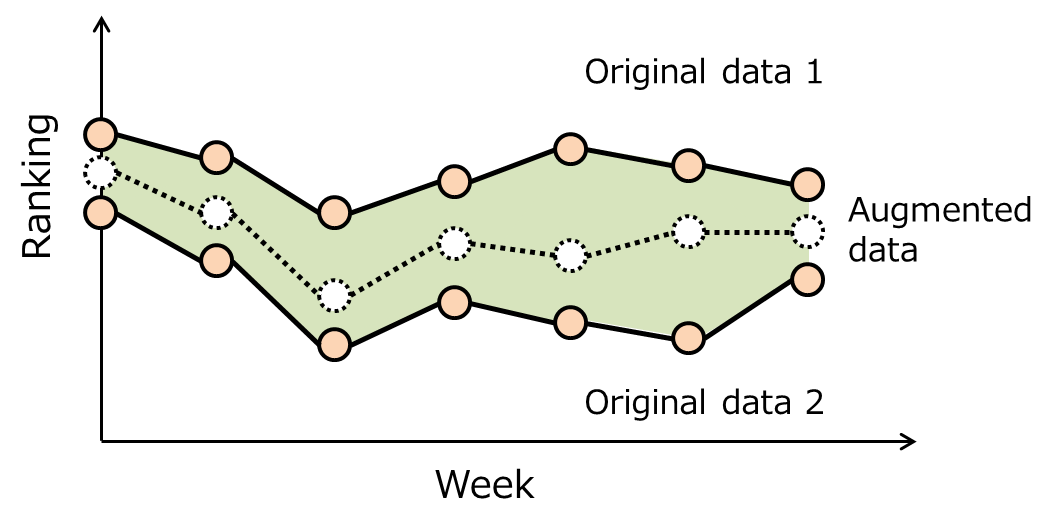
Dataset augmentationは，データを加工してtrainingデータを水増しするテクニックです．主に画像認識や音声認識の性能向上に効果があることが知られています．詳細は，Deep learning bookの7.4節や，機械学習のデータセット画像枚数を増やす方法をご参照ください．本記事の裏テーマは，週刊漫画雑誌の打ち切り予測におけるDataset augmentationの有効性を評価することです．本記事では，下図のような方法でData augmentationを行います．

ざっくり言うと，同じラベルのデータをランダムに２つ選択し，それらのランダムな重み付き平均をとることで，新しいデータを生成します．この背後には，複数の短命作品の中間的な成績（掲載順）を持つ作品も，やはり短命作品だろうという仮定があります．直感的には，そんなに悪くない仮定に思えます．

4. 実装

多層パーセプトロンを管理するためのクラスComicNet()を以下に定義します．ComicNet()は，各種データ（test，validation，およびtrain）の設定，多層パーセプトロンの構築，学習，およびテストを実行します．実装には，TensorFlowを用います．TensorFlowについては，特にプログラマーでもデータサイエンティストでもないけど、Tensorflowを1ヶ月触ったので超分かりやすく解説が詳しいです．

ComicNet()

class ComicNet():
    """ マンガ作品が短命か否かを識別する多層パーセプトロンを管理するクラスです．  
    :param thresh_week：短命作品とそれ以外を分けるしきい値．
    :param n_x：多層パーセプトロンに入力する掲載順の数．
    """
    def __init__(self, thresh_week=20, n_x=7):
        self.n_x = n_x
        self.thresh_week = thresh_week        

以下，各メンバ関数を簡単にご説明します．

4.1 Datasetの設定：configure_dataset()等

ComicNet

    def get_x(self, analyzer, title):
        """指定された作品の指定週までの正規化掲載順を取得する関数です．"""
        worsts = np.array(analyzer.extract_item(title)[:self.n_x])
        bests = np.array(analyzer.extract_item(title, 'best')[:self.n_x])
        bests_normalized = bests / (worsts + bests - 1)
        color = sum(analyzer.extract_item(title, 'color')[:self.n_x]
                    ) /self.n_x
        return np.append(bests_normalized, color)

    def get_y(self, analyzer, title, thresh_week):
        """指定された作品が，短命作品か否かを取得する関数です．"""
        return int(len(analyzer.extract_item(title)) <=  thresh_week)

    def get_xs_ys(self, analyzer, titles, thresh_week):
        """指定された作品群の特徴量とラベルとタイトルを返す関数です．
        　　y==0とy==1のデータ数を揃えて返します．
        """
        xs = np.array([self.get_x(analyzer, title) for title in titles])
        ys = np.array([[self.get_y(analyzer, title, thresh_week)] 
                       for title in titles])

        # ys==0とys==1のデータ数を揃えます．
        idx_ps = np.where(ys.reshape((-1)) == 1)[0]
        idx_ng = np.where(ys.reshape((-1)) == 0)[0]
        len_data = min(len(idx_ps), len(idx_ng))
        x_ps = xs[idx_ps[-len_data:]]
        x_ng = xs[idx_ng[-len_data:]]
        y_ps = ys[idx_ps[-len_data:]]
        y_ng = ys[idx_ng[-len_data:]]
        t_ps = [titles[ii] for ii in idx_ps[-len_data:]]
        t_ng = [titles[ii] for ii in idx_ng[-len_data:]]

        return x_ps, x_ng, y_ps, y_ng, t_ps, t_ng

    def augment_x(self, x, n_aug):
        """指定された数のxデータを人為的に生成する関数です．"""
        if n_aug:
            x_pair = np.array(
                [[x[idx] for idx in 
                  np.random.choice(range(len(x)), 2, replace=False)]
                 for _ in range(n_aug)])
            weights = np.random.rand(n_aug, 1, self.n_x + 1)
            weights = np.concatenate((weights, 1 - weights), axis=1)
            x_aug = (x_pair * weights).sum(axis=1)

            return np.concatenate((x, x_aug), axis=0)
        else:
            return x

    def augment_y(self, y, n_aug):
        """指定された数のyデータを人為的に生成する関数です．"""
        if n_aug:
            y_aug = np.ones((n_aug, 1)) if y[0, 0] \
                else np.zeros((n_aug, 1))
            return np.concatenate((y, y_aug), axis=0)
        else:
            return y

    def configure_dataset(self, analyzer, n_drop=0, n_aug=0):
        """データセットを設定する関数です．
        :param analyzer: ComicAnalyzerクラスのインスタンス
        :param n_drop: trainingデータから除外する古いデータの数
        :param n_aug: trainingデータに追加するaugmentedデータの数
        """
        x_ps, x_ng, y_ps, y_ng, t_ps, t_ng = self.get_xs_ys(
            analyzer, analyzer.end_titles, self.thresh_week)
        self.x_test = np.concatenate((x_ps[-50:], x_ng[-50:]), axis=0)
        self.y_test = np.concatenate((y_ps[-50:], y_ng[-50:]), axis=0)
        self.titles_test = t_ps[-50:] + t_ng[-50:]
        self.x_val = np.concatenate((x_ps[-100 : -50], 
                                     x_ng[-100 : -50]), axis=0)
        self.y_val = np.concatenate((y_ps[-100 : -50], 
                                     y_ng[-100 : -50]), axis=0)
        self.x_tra = np.concatenate(
            (self.augment_x(x_ps[n_drop//2 : -100], n_aug//2), 
             self.augment_x(x_ng[n_drop//2 : -100], n_aug//2)), axis=0)
        self.y_tra = np.concatenate(
            (self.augment_y(y_ps[n_drop//2 : -100], n_aug//2), 
             self.augment_y(y_ng[n_drop//2 : -100], n_aug//2)), axis=0)

configure_dataset()は，まずget_xs_ys()で入力（x_ps，x_ng）とラベル（y_ps，y_ng）と作品名（t_ps，t_ng）を取得します．ここで，短命作品のデータ（x_ps，y_ps，t_ps）数と，継続作品のデータ（x_ng，y_ng，t_ng）数は等しいです．このうち最新100作品をtestデータ，残りの最新100作品をvalidationデータ，あまりをtrainingデータにします．なお，trainingデータを設定する際，合計n_dropの古いデータを除外したあとで，合計n_augの水増しデータを追加します．

4.2 Computation graphの構築：build_graph()

ComicNet

    def build_graph(self, r=0.001, n_h=7, stddev=0.01):
        """多層パーセプトロンを構築する関数です．
        :param r: 学習率
        :param n_h: 隠れ層のノード数
        :param stddev: 変数の初期分布の標準偏差
        """
        tf.reset_default_graph()

        # 入力層およびターゲット
        n_y = self.y_test.shape[1]
        self.x = tf.placeholder(tf.float32, [None, self.n_x + 1], name='x')
        self.y = tf.placeholder(tf.float32, [None, n_y], name='y')

        # 隠れ層（１層目）
        self.w_h_1 = tf.Variable(
            tf.truncated_normal((self.n_x + 1, n_h), stddev=stddev))
        self.b_h_1 = tf.Variable(tf.zeros(n_h))
        self.logits = tf.add(tf.matmul(self.x, self.w_h_1), self.b_h_1)
        self.logits = tf.nn.relu(self.logits)

        # 隠れ層（２層目）
        self.w_h_2 = tf.Variable(
            tf.truncated_normal((n_h, n_h), stddev=stddev))
        self.b_h_2 = tf.Variable(tf.zeros(n_h))
        self.logits = tf.add(tf.matmul(self.logits, self.w_h_2), self.b_h_2)
        self.logits = tf.nn.relu(self.logits)

        # 出力層
        self.w_y = tf.Variable(
            tf.truncated_normal((n_h, n_y), stddev=stddev))
        self.b_y = tf.Variable(tf.zeros(n_y))
        self.logits = tf.add(tf.matmul(self.logits, self.w_y), self.b_y)
        tf.summary.histogram('logits', self.logits)

        # 損失関数
        self.loss = tf.reduce_mean(
            tf.nn.sigmoid_cross_entropy_with_logits(
                logits=self.logits, labels=self.y))
        tf.summary.scalar('loss', self.loss)

        # 最適化
        self.optimizer = tf.train.AdamOptimizer(r).minimize(self.loss)
        self.output = tf.nn.sigmoid(self.logits, name='output')
        correct_prediction = tf.equal(self.y, tf.round(self.output))
        self.acc = tf.reduce_mean(tf.cast(correct_prediction, tf.float32),
            name='acc')
        tf.summary.histogram('output', self.output)
        tf.summary.scalar('acc', self.acc)

        self.merged = tf.summary.merge_all()

入力層では，tf.placeholderで入力テンソル（x）や教師ラベルテンソル（y）をを定義します．

隠れ層では，tf.Variableで重みテンソル（w_h_1，w_h_2）やバイアス（b_h_1，b_h_2）を定義します．ここでは，Variableの初期分布としてtf.truncated_normalを与えています．truncated_normalは，2シグマより外の値を除外した正規分布であり，好んでよく使われます．実は，このtruncated_normalの標準偏差は，モデルの性能を左右する重要なハイパーパラメータの一つです．今回は事前実験の結果を見て，0.01としました．tf.add，tf.matmul，tf.nn.reluを使って，テンソル同士を結合し，隠れ層を形作っていきます．ちなみに，tf.nn.reluをtf.nn.sigmoidに書き換れば，活性化関数としてSigmoidを使うことができます．TensorFlowで使用可能な活性化関数については，こちらをご参照ください．

出力層では，基本的に潜れ層と同様の処理を行います．損失関数tf.nn.sigmoid_cross_entropy_with_logitsの内部に活性化関数（sigmoid）を含むため，出力層では特に活性化関数を使う必要がないことにご注意ください．tf.summary.scalarにtf.Variableを渡すことで，TensorBoardで時変化を確認できるようになります．

最適化アルゴリズムとして，tf.train.AdamOptimizerを使います．TensorFlowで使用可能な最適化アルゴリズムについては，こちらをご参照ください．最終的な出力値logitsを四捨五入し（つまり閾値0.5で判定し），教師ラベルyに対する正解率をaccとして計算しています．最後に，全てのtf.summary.merge_allで全てのログ情報をマージします．

4.3 学習：train()

TensorFlowでは，tf.Session中で学習を行います．必ず，tf.global_variables_initializer()でVariableの初期化を行う必要があります（これがないと怒られます）．

sess.run(self.optimizer)によって，モデルを学習します．sess.runの第一引数は，タプルによって複数指定することが可能です．また，sess.run()時に，辞書形式でplaceholderに値を代入する必要があります．Training時はx_traとx_traを代入し，Validation時はx_valとy_valを代入します．

tf.summary.FileWriterで，TensorBoard用のログ情報を保存できます．また，tf.train.Saverで学習後のモデルを保存できます．

ComicNet

    def train(self, epoch=2000, print_loss=False, save_log=False, 
              log_dir='./logs/1', log_name='', save_model=False,
              model_name='prediction_model'):
        """多層パーセプトロンを学習させ，ログや学習済みモデルを保存する関数です．
        :param epoch: エポック数
        :pram print_loss: 損失関数の履歴を出力するか否か
        :param save_log: ログを保存するか否か
        :param log_dir: ログの保存ディレクトリ
        :param log_name: ログの保存名
        :param save_model: 学習済みモデルを保存するか否か
        :param model_name: 学習済みモデルの保存名
        """
        with tf.Session() as sess:
            sess.run(tf.global_variables_initializer()) # 変数の初期化

            # ログ保存用の設定
            log_tra = log_dir + '/tra/' + log_name 
            writer_tra = tf.summary.FileWriter(log_tra)
            log_val = log_dir + '/val/' + log_name
            writer_val = tf.summary.FileWriter(log_val)        

            for e in range(epoch):
                feed_dict = {self.x: self.x_tra, self.y: self.y_tra}
                _, loss_tra, acc_tra, mer_tra = sess.run(
                        (self.optimizer, self.loss, self.acc, self.merged), 
                        feed_dict=feed_dict)

                # validation
                feed_dict = {self.x: self.x_val, self.y: self.y_val}
                loss_val, acc_val, mer_val = sess.run(
                    (self.loss, self.acc, self.merged),
                    feed_dict=feed_dict)

                # ログの保存
                if save_log:
                    writer_tra.add_summary(mer_tra, e)
                    writer_val.add_summary(mer_val, e)

                # 損失関数の出力
                if print_loss and e % 500 == 0:
                    print('# epoch {}: loss_tra = {}, loss_val = {}'.
                          format(e, str(loss_tra), str(loss_val)))

            # モデルの保存
            if save_model:
                saver = tf.train.Saver()
                _ = saver.save(sess, './models/' + model_name)

4.4 テスト：test()

ComicNet

    def test(self, model_name='prediction_model'):
        """指定されたモデルを読み込み，テストする関数です．
        :param model_name: 読み込むモデルの名前
        """
        tf.reset_default_graph()
        loaded_graph = tf.Graph()

        with tf.Session(graph=loaded_graph) as sess:

            # モデルの読み込み
            loader = tf.train.import_meta_graph(
                './models/{}.meta'.format(model_name))
            loader.restore(sess, './models/' + model_name)

            x_loaded = loaded_graph.get_tensor_by_name('x:0')
            y_loaded = loaded_graph.get_tensor_by_name('y:0')

            loss_loaded = loaded_graph.get_tensor_by_name('loss:0')
            acc_loaded = loaded_graph.get_tensor_by_name('acc:0')
            output_loaded = loaded_graph.get_tensor_by_name('output:0')

            # test
            feed_dict = {x_loaded: self.x_test, y_loaded: self.y_test}
            loss_test, acc_test, output_test = sess.run(
                (loss_loaded, acc_loaded, output_loaded), feed_dict=feed_dict)
            return acc_test, output_test

test()は，学習済みの多層パーセプトロンをテストするメンバ関数です．tf.train.import_meta_graphを使って，学習済みのモデルを読み込みます．testデータ（x_test，y_test）をfeed_dictに与え，sess.runします．

5. 実験

5.1 ハイパーパラメータの調整

TensorBoardでvalidationデータのaccuracy（正解率）とloss（損失関数の出力）を可視化することで，ハイパーパラメータ（学習率$r$とepoch数）をチューニングします．TensorBoardの詳細は公式をご参照ください．簡単のため，本記事では有効数字一桁のみ調整します．また，詳細は割愛しますが，隠れ層の層数（2），隠れ層の活性化関数（ReLU），変数の初期分布の標準偏差（0.01），最適化アルゴリズム（Adam）については，事前実験で簡単に調整済みです．

rs = [n * 10 ** m for m in range(-4, -1) for n in range(1, 10)]
datasets = [
    {'n_drop':0, 'n_aug':0},
    {'n_drop':173, 'n_aug':0},
    {'n_drop':173, 'n_aug':173},
]

wjnet = ComicNet()

for i, dataset in enumerate(datasets):
    wjnet.configure_dataset(wj, n_drop=dataset['n_drop'], 
                            n_aug=dataset['n_aug'])
    log_dir = './logs/dataset={}/'.format(i + 1)
    for r in rs:
        log_name = str(r)
        wjnet.build_graph(r=r)
        wjnet.train(epoch=20000, save_log=True, log_dir=log_dir, 
                log_name=log_name)
        print('Saved log of dataset={}, r={}'.format(i + 1, r))

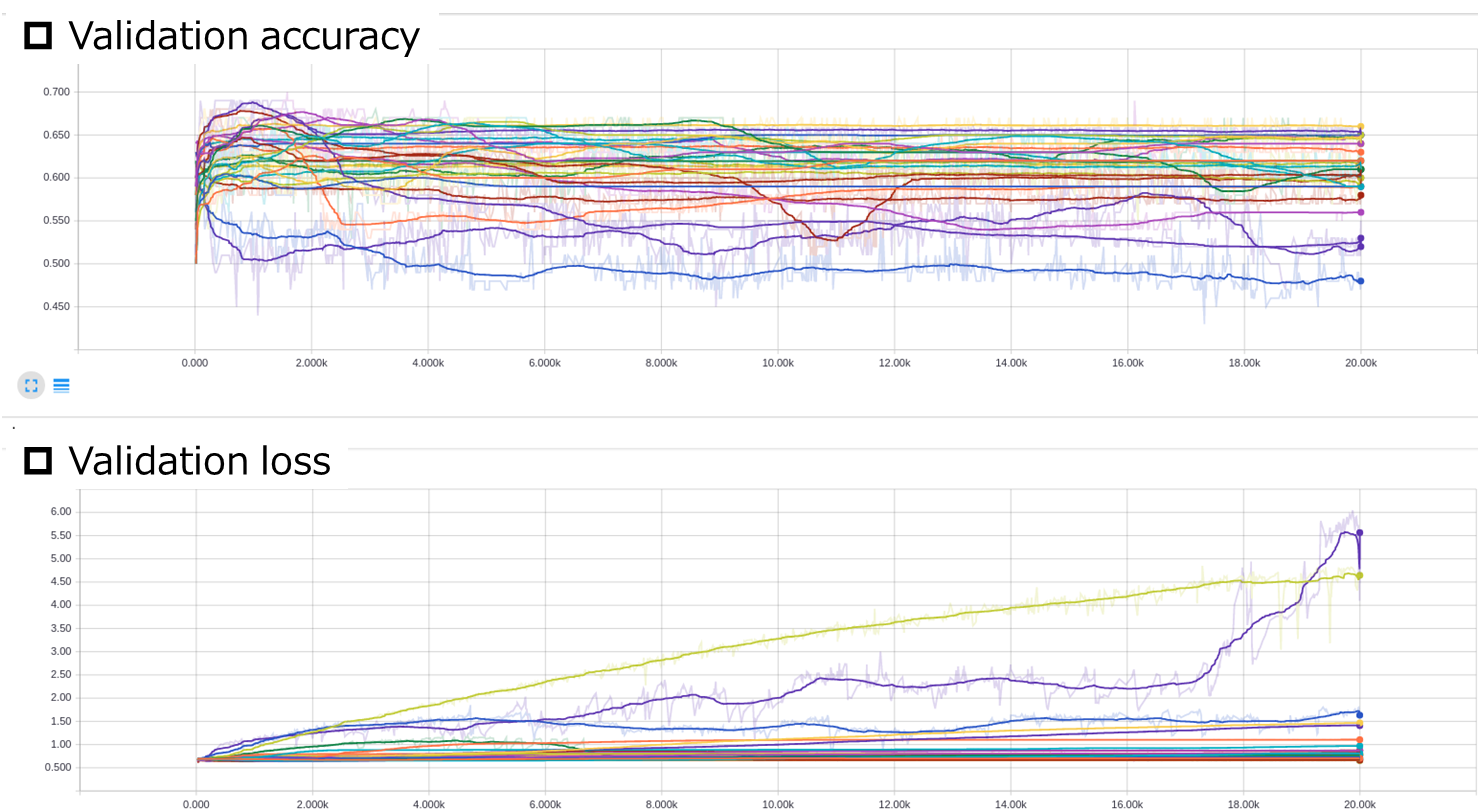
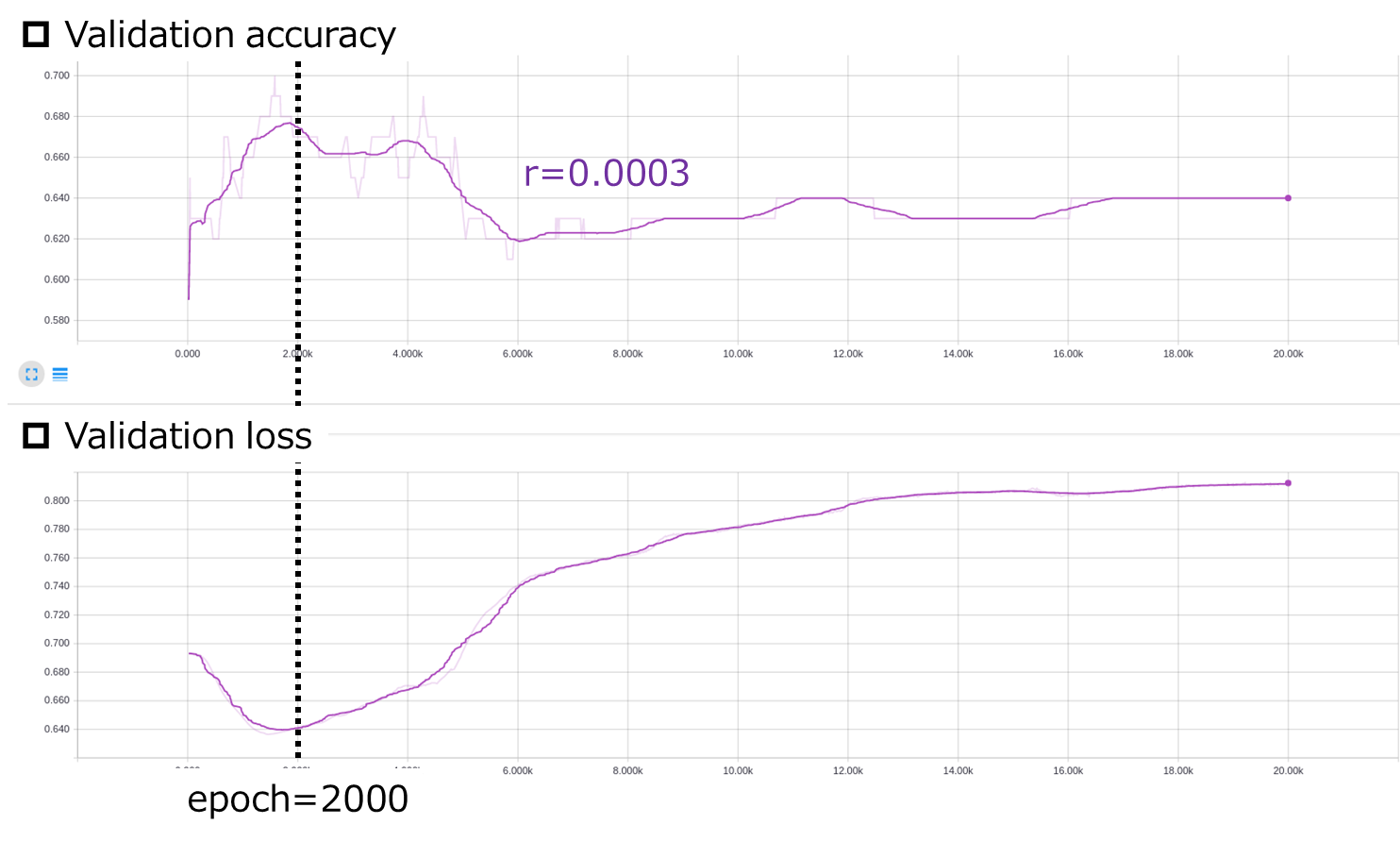
Dataset 1について，validationデータのaccracyとlossをTensorBoardで見てみます．

tensorboard --logdir=./logs/dataset=1/val

横軸はepoch数です．ここから，Validation lossを最小化する$r$と$epoch$を探します．

Dataset 1に関しては，$r=0.0003$，$epoch=2000$が良さそうです．Dataset 2とDataset 3についても同様の処理を行います．

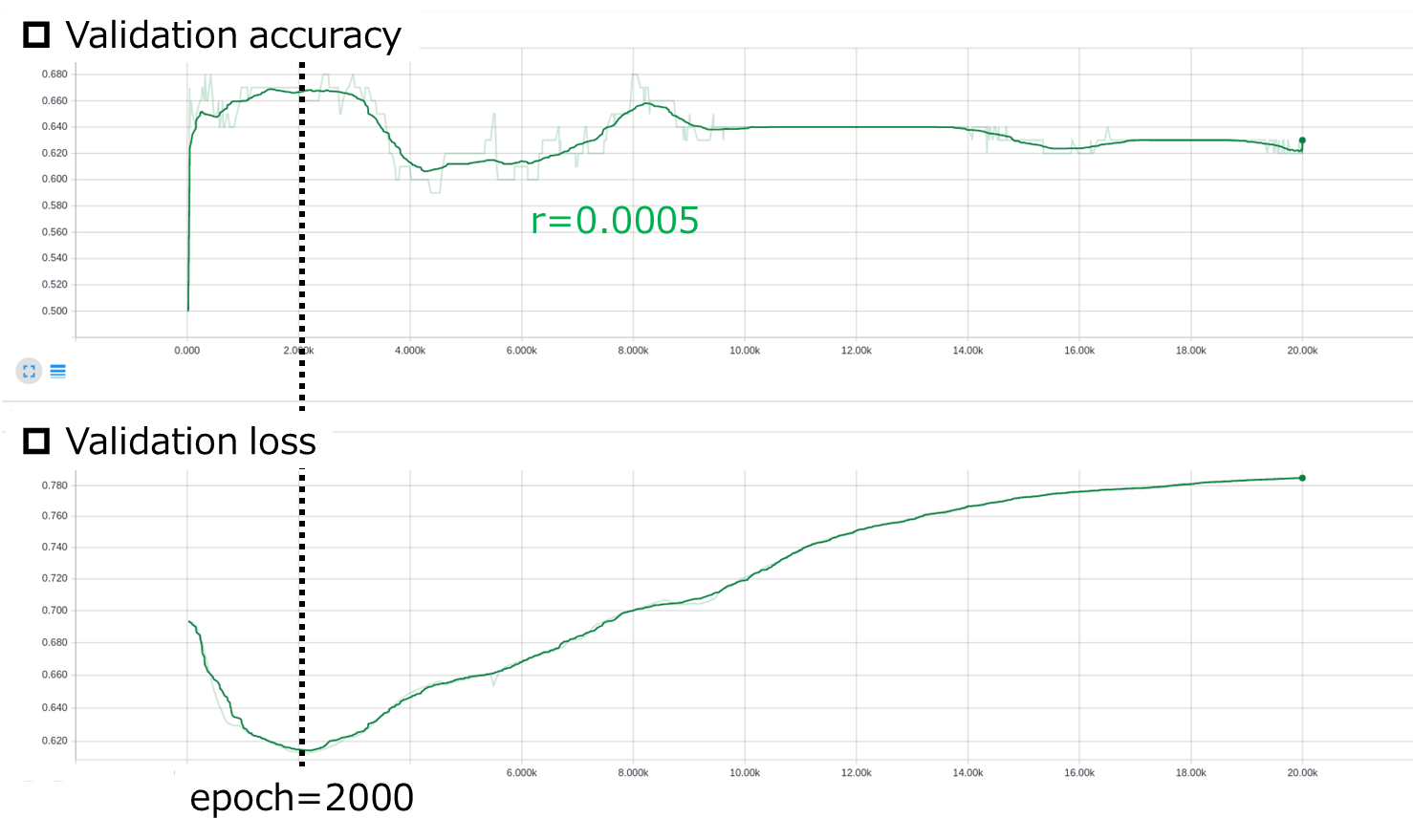
Dataset 2に関しては，$r=0.0005$，$epoch=2000$が良さそうです．

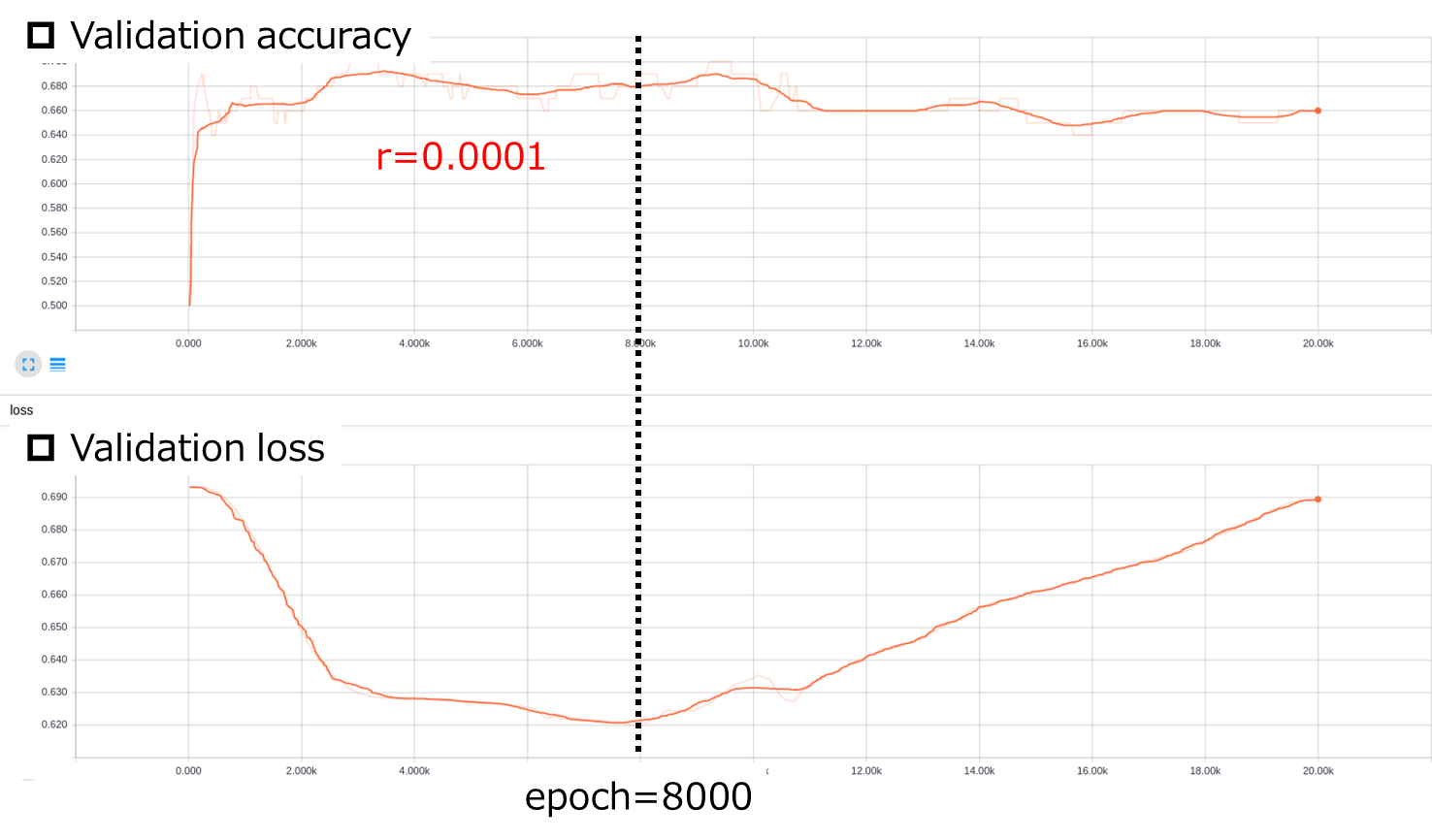
Dataset 3に関しては，$r=0.0001$，$epoch=8000$が良さそうです．

5.2 学習

それぞれのDatasetに対して，上記で調整したハイパーパラメータで学習を行い，モデルを保存します．

params = [
    {'n_drop':0, 'n_aug':0, 'r':0.0003, 
     'e': 2000, 'name':'1: Original'},
    {'n_drop':173, 'n_aug':0, 'r':0.0005, 
     'e': 2000, 'name':'2: Filtered'},
    {'n_drop':173, 'n_aug':173, 'r':0.0001, 
     'e': 8000, 'name':'3: Filtered+Augmented'}
]

wjnet = ComicNet()
for i, param in enumerate(params):
    model_name = str(i + 1)
    wjnet.configure_dataset(wj, n_drop=param['n_drop'],
                            n_aug=param['n_aug'])
    wjnet.build_graph(r=param['r'])
    wjnet.train(save_model=True, model_name=model_name, epoch=param['e'])
    print('Trained', param['name'])

5.3 評価

ComicNet.test()で性能を評価します．

accs = []
outputs = []
for i, param in enumerate(params):
    model_name = str(i + 1)
    acc, output = wjnet.test(model_name)
    accs.append(acc)
    outputs.append(output)
    print('Test model={}: acc={}'.format(param['name'], acc))

plt.bar(range(3), accs, tick_label=[param['name'] for param in params])
for i, acc in enumerate(accs):
    plt.text(i - 0.1, acc-0.3, str(acc), color='w')
plt.ylabel('Accuracy') 

ランダムに分類しても$acc=0.5$となるはずなので，微妙な結果となってしまいました…．FilterとAugmentationの効果が確認できたのは，不幸中の幸いです．

5.4 考察

最も性能の良いモデル３（Filtered + Augmented）の結果をもう少し掘り下げます．

idx_sorted = np.argsort(output.reshape((-1)))
output_sorted = np.sort(output.reshape((-1)))

y_sorted = np.array([wjnet.y_test[i, 0] for i in idx_sorted])
title_sorted = np.array([wjnet.titles_test[i] for i in idx_sorted])

t_ng = np.logical_and(y_sorted == 0, output_sorted < 0.5)
f_ng = np.logical_and(y_sorted == 1, output_sorted < 0.5)
t_ps = np.logical_and(y_sorted == 1, output_sorted >= 0.5)
f_ps = np.logical_and(y_sorted == 0, output_sorted >= 0.5)

weeks = np.array([len(wj.extract_item(title)) for title in title_sorted])
plt.plot(weeks[t_ng], output_sorted[t_ng], 'o', ms=10,
        alpha=0.5, c='b', label='True negative')
plt.plot(weeks[f_ng], output_sorted[f_ng], 'o', ms=10,
        alpha=0.5, c='r', label='False negative')
plt.plot(weeks[t_ps], output_sorted[t_ps], '*', ms=15,
        alpha=0.5, c='b', label='True positive')
plt.plot(weeks[f_ps], output_sorted[f_ps], '*', ms=15,
         alpha=0.5, c='r', label='False positive')
plt.ylabel('Output')
plt.xlabel('Serialized weeks')
plt.xscale('log')
plt.ylim(0, 1)
plt.legend()

上図は，実際の連載期間と分類器の出力の関係を示します．青色は正しく分類できた作品（True）で，赤色は誤って分類された作品（False）です．星は短命作品と分類された作品（Positive），丸は継続作品と分類された作品（Negative）です．青色の作品が多く，またグラフ上の左上から右下に分布が集中するほど，分類性能が優れていると考えられます．

まず，0.75以上の出力がないことが気になります．学習がうまくいっていないのでしょうか？よくわかりません…．次に気になるのが，グラフ右上のFalse positiveです．100週以上連載された一部の人気作品が，短命作品と誤分類されてしまっています．そこで，各分類結果の代表的な作品の掲載順（worst）を比較してみます．

plt.figure(figsize=(12, 8))

plt.subplot(2, 2, 1)
for output, week, title in zip(
    output_sorted[t_ps][-5:], weeks[t_ps][-5:], title_sorted[t_ps][-5:]):
    plt.plot(range(1, 8), wj.extract_item(title)[:7], 
             label='{0} ({1:>3}, {2:.2f})'.format(title[:5], week, output))
plt.ylabel('Worst')
plt.ylim(0, 23)
plt.title('True positive（正しく分類された短命作品）の一部')
plt.legend()

plt.subplot(2, 2, 2)
for output, week, title in zip(
    output_sorted[f_ps], weeks[f_ps], title_sorted[f_ps]):
    if week > 100:
        plt.plot(range(1, 8), wj.extract_item(title)[:7], 
                 label='{0} ({1:>3}, {2:.2f})'.format(title[:5], week, output))
plt.ylim(0, 23)
plt.title('False positive（短命作品と誤分類された継続作品）の一部')
plt.legend()

plt.subplot(2, 2, 3)
for output, week, title in zip(
    output_sorted[f_ng][:5], weeks[f_ng][:5], title_sorted[f_ng][:5]):
    plt.plot(range(1, 8), wj.extract_item(title)[:7], 
             label='{0} ({1:>3}, {2:.2f})'.format(title[:5], week, output))
plt.xlabel('Weeks')
plt.ylabel('Worst')
plt.ylim(0, 23)
plt.title('False negative（継続作品と誤分類された短命作品）の一部')
plt.legend()

plt.subplot(2, 2, 4)
for output, week, title in zip(
    output_sorted[t_ng][:5], weeks[t_ng][:5], title_sorted[t_ng][:5]):
    plt.plot(range(1, 8), wj.extract_item(title)[:7], 
             label='{0} ({1:>3}, {2:.2f})'.format(title[:5], week, output))
plt.xlabel('Weeks')
plt.ylim(0, 23)
plt.title('True negative（正しく分類された継続作品）の一部')
plt.legend()

横軸が掲載週，縦軸が巻末から数えた掲載順となります．凡例は作品名（連載期間，出力値）を表します．False positive（右上）の作品は，True negative（右下）の作品と比較し，7週目までの掲載順の下降傾向が強いことがわかります．逆に言えば，False positive（右上）の作品は，序盤の劣勢を巻き返した人気作品と捉えられます．また，False negative（左下）の作品の7週までの掲載順は下降傾向が穏やかであり，少なくとも私の目には，True negative（右下）の作品のそれと見分けがつきません．誤分類された理由が，なんとなく理解できます．

以下，参考までに全100作品の出力値をプロットします．

labels = np.array(['{0} ({1:>3})'.format(title[:6], week)
                   for title, week in zip(title_sorted, weeks) ])

plt.figure(figsize=(4, 18))
plt.barh(np.arange(100)[t_ps], output_sorted[t_ps], color='b')
plt.barh(np.arange(100)[f_ps], output_sorted[f_ps], color='r')
plt.barh(np.arange(100)[f_ng], output_sorted[f_ng], color='r')
plt.barh(np.arange(100)[t_ng], output_sorted[t_ng], color='b')
plt.yticks(np.arange(100), labels)
plt.xlim(0, 1)
plt.xlabel('Output')
for i, out in enumerate(output_sorted):
    plt.text(out + .01, i - .5, '{0:.2f}'.format(out))

横軸は出力値を表します．作品名の隣の括弧は，連載期間を表します．青色は正しい分類結果，赤色は誤った分類結果を表します．出力値が1に近いほど，短命作品っぽいと判断されたことになります．

6. おわりに

実は，Deep learning foundation nanodegree⁴で学んだことのアウトプット，という位置づけでこの記事を書き始めました．頑なに多層パーセプトロンにこだわったのは，そのためです．やっぱり，実世界の問題に機械学習を適用するのって本当に大変ですね．このテーマじゃなかったら絶対挫折していたと思います．

最終的な性能は残念なものでしたが，データセットのfilteringやaugmentationの効果を確認できたので良かったです．今回決め打ちしたハイパーパラメータ（n_drop，n_aug）を調整すれば，もう少し性能が上がるのではと思います．あるいは，なぜニューラルネットはSVMに勝てないのかでもご指摘のように，SVM等の他の機械学習手法を適用しても良いかもしれません．私は疲れ果てたのでやりませんが．

前編を公開してから，リアルでもネットでも，多くの方からフィードバックを頂きました．日曜プログラマ冥利に尽きます．今後もよろしくお願いします．最後まで読んでくださり，ありがとうございました！

参考文献

本記事の作成にあたっては，以下を参考にさせて頂きました．ありがとうございました！

1. matplotlibで日本語を描画 on Ubuntu：日本語出力について
2. Applying deep learning to real-world problems - Merantix：データラベルに偏りがある場合の対処法について
3. 誤差逆伝播法のノート：多層パーセプトロン全般について
4. なぜ教師あり学習でバリデーションセットとテストセットを分ける必要があるのか？：各種データセットの取り扱いについて
5. Ian Goodfellow and Yoshua Bengio and Aaron Courville, Deep Learning, MIT Press, 2016：Dataset augmentation全般について（7.4節）
6. 機械学習のデータセット画像枚数を増やす方法：画像データに対するDataset augmentationについて
7. 特にプログラマーでもデータサイエンティストでもないけど、Tensorflowを1ヶ月触ったので超分かりやすく解説：TensorFlowについて
8. TensorBoard：TensorBoardを使ったハイパーパラメータ調整について
9. なぜニューラルネットはSVMに勝てないのか：今後の研究方針について

---

1. ジャンプ編集部は「必ずしも読者アンケートの結果だけを考慮しているわけではない」と，アンケート至上主義を否定したようです．「ジャンプ」編集部がアンケート至上主義の噂を否定も…読者は複雑 ↩

2. 前述したように，実際には，ジャンプ編集部は様々な要素を考慮して打ち切り作品を決定されています．本記事は，あくまでも一ジャンプファンの妄想として，ご理解頂ければと思います． ↩

3. じゃあSVM使えばいいじゃんというご指摘はごもっともです．今回はお勉強のため，パーセプトロンにこだわってみました． ↩

4. いわゆる3月生です．よろしくお願いします． ↩