これはWebGL Advent Calendar 2015 23日目の記事（の代打¹）です。

また、WebGL Advent Calendar 2015 15日目の記事である「これがGPUの力！Three.jsによる“リアルタイム”なレイトレーシング」の続編です。

はじめに

今夜は雪だそうですね。こんな寒い日にはGPUをぶん回して暖をとりましょう！

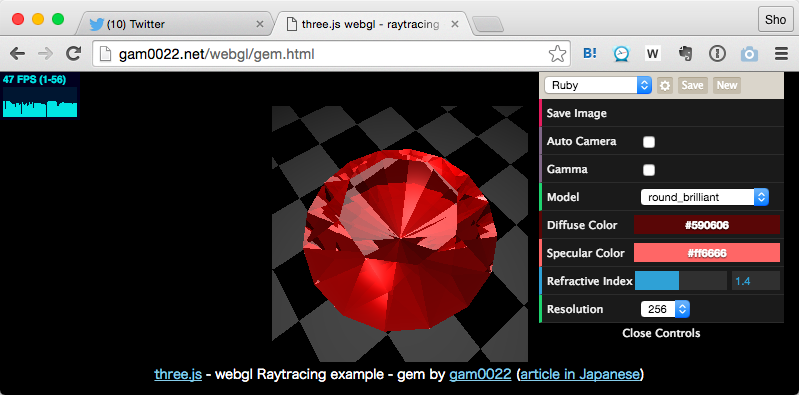
光の屈折をシミュレートすることで、輝く宝石をWebGLでレンダリングする「gem」という作品（技術デモ）をつくりました。レイトレーシングをGLSLのフラグメントシェーダで実装することで、GPUの並列計算を利用したリアルタイムな描画を実現しています。

WebGLで動くので、次のリンクを開くとブラウザ上でそのまま動作します。PCだけでなくiPhone6でも動作を確認しています。

webgl Raytracing example - gem

宝石の屈折率、色（拡散反射・鏡面反射）、宝石の形状、自動カメラ、ガンマ補整など、各種パラメータを変更できます。負荷が重い場合は一番下の「Resolution（解像度）」を128にしてください。また一番上からパラメータのプリセットを選択できます。

宝石と屈折

宝石のように透明な物体を描画するためには、屈折の計算が必要になります。1回までの屈折であれば、ポリゴンのラスタライズ方式でも環境マッピングを用いて高速にレンダリングできます。

次の図は宝石内部での光の反射と屈折の様子です。宝石の輝きは宝石の内部での光の反射と屈折により生じます。そのため、複数回の屈折をシミュレートしなければ、宝石の輝きは再現できません。

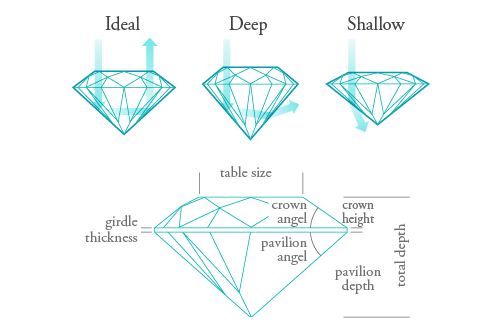
この図はjewelry-tanigawa.comから引用させていただきました。

複数回の屈折を行うためには、ラスタライズ方式ではなく、レイトレーシングが必要になります²。レイトレーシングをするためには膨大な計算が必要ですが、GLSLのフラグメントシェーダで実装することで、GPUの並列計算を利用したリアルタイムに近い速度のレンダリングを実現しました。

実行結果

あらためて最初の節で紹介した「gem」の実行結果を見てみましょう。

これは「Round Brilliant」という形状です。宝石の内部で光が反射と屈折を繰り返すことで、このような結果になります。この例だと、MacBookAirでも256x256の解像度で60fps出ました。手元のiPhone6でも20fps前後でした。

「Barion」と呼ばれる形状です。エメラルドグリーンを意識した色（#084d04/#acff9b）に調節しました。

「Oval Brilliant」という形状です。トパーズを意識した色（#4f5906/#ff6800）に調整しました。

これも「Round Brilliant」ですが、1つ目よりも上部のクラウンと呼ばれる箇所が薄いバージョンになります。

「Regular Octahedron（正八面体）」です。色を#0b024c/#ffffff にして、Refractive Index（屈折率）は1.1と低めにしました。エヴァンゲリオンのラミエルっぽいですね。面数が8と少ないため、MacBookAirでもフルスクリーンで60fpsでうごきます。

実装の概要

詳細な実装について解説する前に、概要を述べておきます。

WebGLのライブラリであるthree.jsで実装
three.jsのシーンとしてはPlaneが1枚あるだけ
- Planeのシェーディング（色の塗り方）処理として、レイトレーシングを実装
objファイルを用意すれば様々な形状をレンダリング可能
- CPU（JavaScript)からGPU(GLSL)に動的に形状情報を橋渡し
- CPUからGPUに渡せるデータのサイズには厳しい制限がある
  - 頂点情報を浮動小数データテクスチャとして渡すことで制限を回避
three.jsの資産を活かして、objファイルのパースやカメラのコントロールはthree.jsに丸投げ

フラグメントシェーダでレイトレを実装するとは

GLSLのフラグメントシェーダとしてレイトレーシングを実装するとはどういうことでしょうか？

実装の概要で述べたとおり、three.jsのシーンとしてはPlaneが1枚があるだけです。Planeの塗り方を計算する処理として、フラグメントシェーダ（GPUで動作するポリゴンのピクセルの塗り方を決めるプログラム）でレイトレーシングを実装しました。

Planeの塗り方を計算する処理として、3D空間を描画するというアプローチは、前回の記事と全く一緒です。THREE.RawShaderMaterialを適用してフラグメントシェーダでゴリゴリとレイトレーシングを実装しています。前回の記事の繰り返しになってしまうので、今回の記事ではこのアプローチについては深く解説しません。

レイトレーシングって何だろう？という方は、先にdoxasさんの「WebGL と GLSL で気軽にレイトレーシングに挑戦してみよう！」という記事を読むことをオススメします。レイトレーシングのGLSL実装について、基礎から解説されています。

前回の記事はレイトレーシングの中でもレイマーチング（スフィアトレーシング）という方法を利用しました。レイマーチングでは、シーンを距離関数で定義して、レイの先端が物体表面にたどり着くまでループを繰り返して衝突判定します。

今回は一般的に知られるレイトレーシングのように、解析的な衝突判定にしました。宝石のobjファイルを読み込んで表示するという都合上、距離関数でシーンを定義するのは難しいからです。

レイトレーシングでもレイマーチングでもシーンとレイ（半直線）の衝突判定が肝になります。

今回はTomas Mollerの手法を用いて、ポリゴン（三角形）とレイ（半直線）の衝突判定を実装しました。

Tomas Mollerの手法は、ポリゴンとレイの衝突判定としては高速で一般的に使われるアルゴリズムです。自分がGLSLで実装する際に参考にした資料を紹介しておきます。

次のコードはTomas Mollerの手法をGLSL実装したものです。

GLSLによるポリゴン（三角形）とレイ（半直線）の衝突判定

// 3次正方行列の行列式をクラメルの公式で計算する
float det( vec3 a, vec3 b, vec3 c ) {
    return (a.x * b.y * c.z)
            + (a.y * b.z * c.x)
            + (a.z * b.x * c.y)
            - (a.x * b.z * c.y)
            - (a.y * b.x * c.z)
            - (a.z * b.y * c.x);
}

// ポリゴン（三角形）とレイ（半直線）の衝突判定する
void rayIntersectsTriangle( vec3 origin, vec3 ray, vec3 v0, vec3 v1, vec3 v2, inout Intersect nearest ) {

    vec3 invRay = -ray;
    vec3 edge1 = v1 - v0;
    vec3 edge2 = v2 - v0;

    float denominator =  det( edge1, edge2, invRay );
    if ( denominator == 0.0 ) return;

    float invDenominator = 1.0 / denominator;
    vec3 d = origin - v0;

    float u = det( d, edge2, invRay ) * invDenominator;
    if ( u < 0.0 || u > 1.0 ) return;

    float v = det( edge1, d, invRay ) * invDenominator;
    if ( v < 0.0 || u + v > 1.0 ) return;

    float t = det( edge1, edge2, d ) * invDenominator;
    if ( t < 0.0 || t > nearest.distance ) return;

    nearest.isHit    = true;
    nearest.position = origin + ray * t;
    nearest.distance = t;
    nearest.normal   = normalize( cross( edge1, edge2 ) ) * sign( invDenominator );
    nearest.material = DIAMOND_MATERIAL;
    nearest.isFront  = invDenominator > 0.0;

}

1つ目の資料のJavaScriptによる実装をGLSLに移植したものになりますが、3つ工夫をしました。

1つ目の工夫について。除算コストは乗算コストより大きいことから、denominatorの除算を、事前にdenominatorの逆数を計算することで、乗算に置き換えて，コストを削減しました。

2つ目の工夫について。今回は物体を透過させて描画するので、背面からの衝突も検知する必要があります。そのため、denominatorが負の場合も衝突したとみなすようにしました。表裏の判定は最後にdenominatorの符号をチェックするようにしました。

3つ目の工夫について。背面の場合は法線を反転させる処理が必要です。一般的にGPUで計算する場合にはifなどの分岐のコストが大きいので、条件分岐を避けるために、組み込みのsignという組み込みメソッドを利用するようしました。

レイトレーシングにおける屈折の実装

今回のテーマは「屈折」です。本節ではレイトレーシングにおける屈折の実装について述べます。

屈折の方向の計算には組み込み関数の`refract`をつかう

GLSLではrefractという屈折のベクトルを計算する組み込み関数があるので、これを利用しました。

https://www.opengl.org/sdk/docs/man/html/refract.xhtml

入射ベクトル、法線ベクトル、屈折率を引数にして、屈折ベクトルを計算します。全反射の判定も可能で、全反射の場合は0ベクトルが返ります。

衝突後のレイの原点を修正する方向の注意点

レイトレーシングで反射をする場合、レイと物体の交点を反射用のレイの原点として、再度レイを飛ばします。

しかし、交点をそのまま原点にしてしまうと、交点の位置で衝突していると誤判定されて、レイが進まないことがあります。これを回避するために、法線方向にむかってレイの原点をずらす必要があります。

ここで注意点なのですが、屈折の場合には、法線の逆方向、つまり物体の内側にずらさなくてはいけません。屈折の場合は物体の内部を通過するレイとなるので、当然といえば当然ですね。

屈折率の反転

レイが空気中から宝石内部に突入する場合と、宝石内部から空気中に脱出する場合では、屈折率を反転する必要があります。

「レイが脱出するとき」の屈折率は「レイが突入するとき」の屈折率の逆数にしなくてはなりません。

レイが突入した OR 脱出したの判定は、rayIntersectsTriangle関数で計算したisFrontを利用します。

今回は使用した宝石の形状はソリッドモデルなので、表からポリゴンに衝突したときにはレイの突入、裏からポリゴンに衝突したときにはレイの脱出であるという法則が成り立ちます。

GLSLで再帰が使えない制約について

GLSLでは再帰が使えないという制約があります。反射しか考慮しない場合にはループだけで処理できるのですが、反射と屈折の両方を実現するためには、再帰的に反射方向のレイと、屈折方向のレイをそれぞれトレーシングする必要があるので、ループだけでは処理できません。

苦肉の策として、宝石に関しては反射の計算は省いてしまい、全反射のときだけ反射をするようにしました。反射を考慮していませんが、ある程度はそれらしい結果になったと思っています。

浮動小数データテクスチャでCPUからGPUに大量の頂点情報を送る

CPU（JavaScript）からGPU（GLSL）へデータを渡すにはuniformを使います³。

モデルの頂点は3次元のベクトル（vec3）です。宝石のモデルの形状情報をシェーダに渡すためには、モデルのデータをトライアングルリスト⁴に変換してvec3の1次元配列であるv3vをuniformで渡すというのが最もシンプルな実装です。

しかし、uniformで渡せるデータサイズには厳しい制限があります。今回もまずはv3vで頂点を渡すような実装にしたのですが、環境によっては面数100くらいでtoo many uniformsというエラーになってしました。

そこでv3vではなく、テクスチャの画素値として頂点情報を詰めることにしました。
つまり、画素値のRGB値をそれぞれ頂点のXYZとして、CPUからGPUに頂点情報を渡す作戦です。

通常のテクスチャでは精度が足りなかったので、浮動小数データテクスチャを利用することにしました。

通常のテクスチャは1ピクセルあたりRGBAそれぞれUint8（符号無し整数）の8bit、合計32bitが割り当てられます。浮動小数データテクスチャでは1ピクセルあたりRGBAそれぞれFloat32（浮動小数）の32bit、合計128bitが割り当てられます。

浮動小数データテクスチャはWebGLの拡張機能という位置づけで、実装されていることの保証がないAPIとなりますが、実際には多くのデバイスで利用可能のようです。

three.jsから浮動小数データテクスチャを利用する方法については、JavaScriptoon2というC89本の「SIMD.jsを超える！？WebGLで100万パーティクルへの挑戦」という記事に詳しく書かれています。

three.jsの資産の活用

three.jsでは3D関連の役に立つコードが既にたくさん存在します。ですので、今回も利用できるものは積極的に利用しました。

例えば、objファイルの読み込みにTHREE.OBJLoaderを利用しました。

また、自由モード（マウスのドラッグなで視点の移動ができる）でのカメラの制御には、THREE.OrbitControlsを利用しました。カメラの原点と向きをuniformを使ってフラグメントシェーダに渡す設計にしました。

おわりに

ここまでお付合いいただき、本当にありがとうございます。

本当は宝石をたくさん並べてみたかったのですが、負荷的に厳しすぎて断念しました。

GLSLのフラグメントシェーダでレイトレーシングを実装しようとすると、それなりに制約があるので大変ですが、試行錯誤の過程がとても楽しいと思います。

みなさんもGLSLでレイトレーシングしてみませんか？

もう2016/1/29ですが、WebGL Advent Calendar 2015の23日担当の人が投稿しなかったので代理で投稿しました。本来であれば、WebGLがWebテクノロジー部門ランキングで余裕のNo.1になるはずでしたが、23日に欠番があったため、25日間全ての参加登録がされているカレンダーを対象としたを満たせずランキング外(ストック数、購読数)となっていました。個人的にとても無念だったので、代わりに投稿するに至りました。【追記】見事WebGLがランキング1位（ストック数、購読数）になりました ↩
レイトレーシングを使わない2回屈折を考慮した描画の研究も存在します。しかし、背面と全面に分けて2回屈折を実現する手法では、今回の宝石のように内部で反射と屈折をするケースや3回以上の屈折にはおそらく対応できないと考えています。 ↩
他にはattributeなどもありますが、それは本筋ではないので割愛します。気になる方はシェーダの記述と基礎を読んで下さい。 ↩
トライアングルリストとは、ポリゴンを構成する3頂点を並べたものです。面数が100の形状であれば、100*3 = 300 要素のトライアングルリストになります。重複する頂点分はメモリ的には無駄になりますが、頂点と面を別々に持つよりも、フラグメントシェーダ側から頂点を取り出す実装が簡単になります。 ↩

これがGPUの力！three.jsによる“リアルタイム”なレイトレーシング 〜宝石編〜