これはWebGL Advent Calendar 15日目の記事です。
【2016/01/29 追記】続編である「これがGPUの力!three.jsによる“リアルタイム”なレイトレーシング 〜宝石編〜」を公開しました。
はじめに
Three.jsからGPUをつかって、リアルタイムなレイトレーシングを実装できたので紹介します。
iPhone6などの携帯端末でも動作するくらい軽量です。次のリンクから動作の様子をご覧になってください!
マウス移動によって、上からの視点にもできます。
無数の球体がずら〜っと並ぶ様子は、ちょっと壮観ですね!?
一般的にレイトレーシングを行うためには、膨大な計算が必要です。
ソフトウェアで実装した場合、数個の球体を配置しただけでもリアルタイムに処理するのは困難です。
2010年の記事によると、Fortranで実装した鏡面反射した球体を敷き詰めたシーンの描画に20分かかったとありました。
上のシーンでは球体を無数に配置していますが、携帯端末のような貧弱なスペックでもリアルタイムに動作します。
これを実現するのが、GPUによる並列計算と後述するレイマーチングという手法です!
次の節からはThree.jsからGPUを利用する方法や、レイマーチングの基本概念などについて紹介します。
既にレイマーチングを実装したことのある方は、レイマーチングの発展的な話から読んでください。
レイトレーシングをGPU実装する
WebGLからGPUを利用するためには、GLSLというシェーダ言語を記述します。
シェーダはWebGLなどのグラフィックAPIの描画方法を制御するプログラムです。
WebGLでは、頂点シェーダとフラグメントシェーダの2種類のシェーダを利用できますが、
上で紹介したシーンは、ほぼすべてをフラグメントシェーダで実装しています。
フラグメントシェーダは画面上のピクセルの色を操作するためのシェーダです。本来はシェーディング(陰影で立体感を出す)などのポリゴン上のピクセルの色の塗り方を決める処理を記述します。
上のシーンは複雑に見えますが、Three.jsのシーンとしては1枚の板(PlaneBufferGeometry)が配置されているだけです。
フラグメントシェーダを記述することで、1枚の板のポリゴンの色の塗り方を計算する処理として、球体と床を描き込んでいます。
GPUをつかった並列計算
GPUは並列計算を得意としますが、並列化のために各頂点やピクセルの処理が独立でなくてはいけないという制約があります。
つまり、フラグメントシェーダであれば、隣のピクセルを読み取れません。
レイトレーシングではピクセル単位でレイを追跡しピクセルの色を決定する処理を行います。そのため、レイマーチングでは原理的にピクセルごとの処理は独立しています。
つまり、フラグメントシェーダとレイトレーシングは非常に相性が良いわけです。
今回もフラグメントシェーダの中でカメラやレイを定義して、ゴリゴリとレイトレーシングをGLSLで実装しました。
Three.jsからシェーダをつかう
Three.jsは有名なWebGLのラッパーライブラリです。
シェーダを利用するような低レベルが記述が必要なケースでは、Three.jsのような高レベルなライブラリは不向きではないのか?と考える方もいるかもしれません。
Three.jsは3DCGを手軽に扱うための高レイヤーなインターフェースを提供する一方で、シェーダを直接制御するような低レイヤー向けのインターフェースも提供しています。この柔軟性の高さがThree.jsの魅力の1つです。
Three.jsからシェーダを利用するためには、ShaderMaterialというクラスを利用します。
次のコードでは、Three.jsを利用して、1枚の板のジオメトリを作り、それに頂点シェーダとフラグメントシェーダを設定したマテリアルを適用しています。
geometry = new THREE.PlaneBufferGeometry(2.0, 2.0);
material = new THREE.ShaderMaterial({
uniforms: {
time: { type: "f", value: 0.0 },
resolution: { type: "v2", value: new THREE.Vector2(512.0, 512.0) },
mouse: { type: "v2", value: mouse }
},
vertexShader: document.getElementById('vertex_shader').textContent,
fragmentShader: document.getElementById('fragment_shader').textContent
});
mesh = new THREE.Mesh(geometry, material);
scene.add(mesh);
ShaderMaterialのコンストラクタのオプションとして、vertexShaderに頂点シェーダを、fragmentShaderにフラグメントシェーダを文字列として指定しています。
ここでdocument.getElementById('vertex_shader').textContentの記述が気になると思います。
実際にHTMLを眺めると分かりますが、各シェーダはscriptタグの中に記述しています。
JavaScriptではヒアドキュメントが使えないため、scriptタグにコードを書いて、getElementByIdで取り出すという方法をとりました。
ちなみに、上記の処理をThree.jsを使わずに実装しようと思うと200行くらいのJavaScriptをゴリゴリ実装する必要があるので、興味のある方は比較してみたら良いでしょう。Three.jsの偉大さを味わえます。
JavaScriptのコードの全体はこちらにあります。短いので、さほど苦労せずに読めるかと思います。
レイトレーシングのひとつ、レイマーチング
タイトルでは「レイトレーシング」という言葉を使いましたが、厳密には「レイマーチング」という手法を用いました。
まずレイマーチングはレイトレーシングの1種です。
この2つの大きな違いは、レイとオブジェクトの衝突判定にあります。
一般的なレイトレーシングではベクトル計算を駆使して、解析的な方法で衝突判定を行います。
一方でレイマーチングでは距離関数を用いて衝突判定を行います。距離関数とは、任意の点からオブジェクトの表面までの最短距離を返す関数です。
距離関数を利用してシーンの形状を定義しているので、カメラ座標をmod関数でループさせれば、同じ形状を無限に繰り返す repetition が可能です。
以下は、レイマーチングにおけるレイとオブジェクトの衝突判定のアルゴリズムです。
この3つの手順のセットを「マーチング・ループ」とも呼びます。
レイマーチングでは、レイの先端がオブジェクトに衝突するまで、マーチング・ループを繰り返します。
- レイの先端からシーン上の全てのオブジェクトへの最短距離dを距離関数から求める
- レイの先端を距離dだけ進める
- 距離dが十分に小さな値であれば、レイの先端がオブジェクトと衝突したと判定し、ループを抜ける
- ループ回数が閾値を超えたら、レイはどのオブジェクトにも衝突しないと判定し、ループを抜ける
- 1に戻る
レイマーチングの具体例
前節で紹介したアルゴリズムを踏まえつつ、具体例を使ってマーチング・ループを説明します。
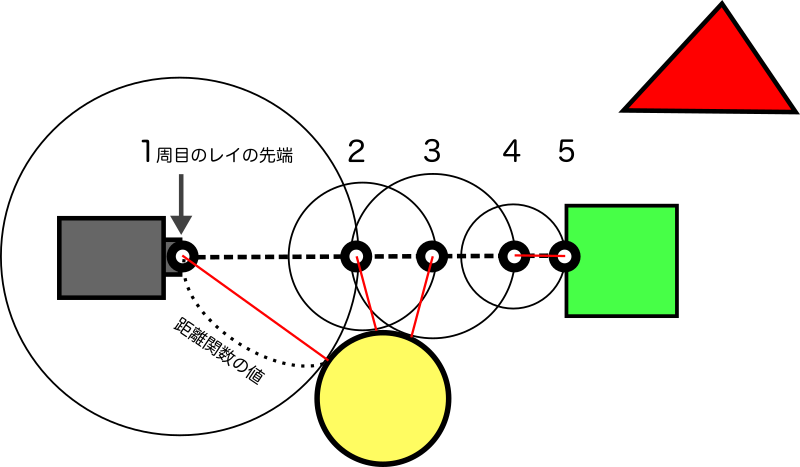
このシーンでは、カメラから見て球体、箱、三角形の順にオブジェクトが並んでいます。
それでは、カメラの座標を起点としてマーチング・ループを繰り返し適用しながら、レイの先端を進めていきます。
1周目のループでは、レイの先端はカメラの座標にあります。従って、レイの先端と最も近いオブジェクトは球体ですので、球体との距離dだけレイの先端を進めます。
同様に2周目と3周目のループでも、レイの先端に最も近いオブジェクトは球体なので、球体との距離dだけレイの先端を進めます。
ところが4周目のループでは、レイの先端に最も近いオブジェクトが球体から箱へと変化します。
そこで今度は箱との距離dだけレイの先端を進めます。
するとレイの先端は箱の表面に到達しますので、5周目のループではdが十分小さくなり、レイの先端とオブジェクトが衝突したと判定されてマーチング・ループを抜けます。
こうして、距離関数だけでレイとオブジェクトの衝突判定ができました。
今回の距離関数を利用したレイマーチングは、等距離でレイと進めるレイマーチングを区別するために、スフィアトレーシングと呼ばれることもあるようです。
レイの進む距離がスフィア(球)の半径になるので、スフィアトレーシングです。
レイマーチングを深く学びたい方へ
簡単にレイマーチングの概要だけは説明しましたが、これだけの説明では理解が難しいと思います。
ここまでの説明の目的は、レイマーチングを知らない人向けになんとなく雰囲気を掴んでもらうことです。
1エントリーでは話しきれないため、実際の実装や注意点は省いて説明しました。
レイマーチングをもっと知りたい!という方は、以下のサイトと本をオススメします。
wgld.orgというサイトでは、レイマーチングについて図や詳しい解説をまじえて分かりやすく説明されています。私自身もこのサイトでレイマーチングを勉強しました。超オススメです!
JavaScriptoon2はC89のコミケで発売するWebフロントエンド本です。
私はこの本の「シェーダだけで世界を創る!Three.jsによるレイマーチング」という章を執筆させていただいております。
読者の対象は「Three.jsの基本が分かるけれどもプログラマブルシェーダ(カスタムシェーダ)は使ったことのない!」という方です。
シェーダの基本から説明していきますので、**今までの説明は良く分からなかったけど、レイマーチングが気になって夜も眠れないという方はぜひ買って下さい!!**お願いします!!
前節で軽く紹介したThree.jsからシェーダをつかう方法についても、もっと詳しく書きました。
レイマーチングの発展的な話
ここからはレイマーチングを既に実装したことがある人を対象として、レイマーチングで特定のオブジェクトだけに色を付けるための方法と、鏡のように周囲の背景を写り込ませる鏡面反射の実現方法について紹介します。
すこし発展的な内容となるので、レイマーチングの基本を理解してから読むことをオススメします。
特定のオブジェクトだけに色をつける
レイマーチングで特定のオブジェクトだけに色をつけるためには工夫が必要です。
レイマーチングではシーンの形状を距離関数で表現していて、どのオブジェクトに衝突したのかを後から知ることができないからです。
今回は色の塗り分けを実現するために、距離関数に加えて、色を返す関数を実装しました。
float sceneDist(vec3 p) {
return min(
sphereDist(p, 1.0),
floorDist(p)
);
}
vec4 sceneColor(vec3 p) {
return minVec4(
// 3 * 6 / 2 = 9
vec4(hsv2rgb(vec3((p.z + p.x) / 9.0, 1.0, 1.0)), sphereDist(p, 1.0)),
vec4(vec3(0.5) * checkeredPattern(p), floorDist(p))
);
}
sceneDistは通常の距離関数で、sceneColorは色と距離を返す関数です。
sceneColorはvec4型を返すように設計しました。
返り値のベクトルの.rgbに色情報を、.aを距離情報を格納します。
minVec4は独自に定義した関数で次のように実装しました。距離の成分を比較して、小さい方のベクトルを返します。
vec4 minVec4(vec4 a, vec4 b) {
return (a.a < b.a) ? a : b;
}
次のgetRayColor関数はレイの原点と方向を入力として、ピクセルの色を返す関数です。
平行光源からのPhongの反射とソフトシャドウを計算しています。
また深度に比例して暗くする処理を行なっています。
vec3 getRayColor(vec3 origin, vec3 ray, out vec3 p, out vec3 normal, out bool hit) {
// marching loop
float dist;
float depth = 0.0;
p = origin;
for(int i = 0; i < 64; i++){
dist = sceneDist(p);
depth += dist;
p = origin + depth * ray;
if (abs(dist) < EPS) break;
}
// hit check and calc color
vec3 color;
if (abs(dist) < EPS) {
normal = getNormal(p);
float diffuse = clamp(dot(lightDir, normal), 0.1, 1.0);
float specular = pow(clamp(dot(reflect(lightDir, normal), ray), 0.0, 1.0), 10.0);
float shadow = getShadow(p + normal * OFFSET, lightDir);
color = (sceneColor(p).rgb * diffuse + vec3(0.8) * specular) * max(0.5, shadow);
hit = true;
} else {
color = vec3(0.0);
}
return color - pow(clamp(0.05 * depth, 0.0, 0.6), 2.0);
}
前半のマーチング・ループ(// marching loop)では、sceneDist関数を使って衝突判定を行なっています。
そして後半の // hit check and calc color の処理では、衝突した時にだけsceneColor関数を呼び出して、衝突したオブジェクトの色を取得しています。
補足をするとsceneDist(p) == sceneColor(p).aになっています。
そのためsceneColor関数だけでもマーチング・ループを行うことも可能ですが、それでは色の計算が無駄になってしまいます。
今回の実装ではsceneDistとsceneColorで関数を別々にすることで、高速化しています。
うまく工夫すれば、距離関数を2重に定義することを避けられそうですが、GPUは分岐予測が苦手なので今回のケースではこの実装が有効だと考えています。
鏡面反射させるには
鏡面反射を計算するためには、オブジェクトとの衝突後に反射ベクトルを求めてさらにレイを追跡します。
このような処理は再帰関数を使うと綺麗に実装できます。
ところが、GLSLは再帰関数をサポートしていないので、うまくループに置き換える必要があります。
次のコードはフラグメントシェーダのmain関数で、ここでカメラとレイの定義を行い、反射ベクトルから反射のレイの計算も行なっています。
void main(void) {
// fragment position
vec2 p = (gl_FragCoord.xy * 2.0 - resolution) / min(resolution.x, resolution.y);
// camera and ray
vec3 cPos = vec3(mouse.x - 0.5, mouse.y * 4.0 - 0.2, time);
vec3 cDir = normalize(vec3(0.0, -0.3, 1.0));
vec3 cUp = cross(cDir, vec3(1.0, 0.0 ,0.0));
vec3 cSide = cross(cDir, cUp);
float targetDepth = 1.3;
vec3 ray = normalize(cSide * p.x + cUp * p.y + cDir * targetDepth);
vec3 color = vec3(0.0);
vec3 q, normal;
bool hit;
float alpha = 1.0;
for(int i = 0; i < 3; i++) {
color += alpha * getRayColor(cPos, ray, q, normal, hit);
alpha *= 0.3;
ray = normalize(reflect(ray, normal));
cPos = q + normal * OFFSET;
if (!hit) {
break;
}
}
gl_FragColor = vec4(color, 1.0);
}
最後のforループが反射ベクトルの再帰をループに置き換えたものです。
衝突をした頂点をレイの原点とし、反射ベクトルをレイの向きとして、再度レイ追跡によるピクセルの計算を行なっています。
alphaは反射のループの度に小さくなっていく係数で、これで光が反射によって弱まっていくのを表現します。
また、反射レイを求める際にも注意点があります。
レイマーチングではレイの先端がオブジェクトに衝突してしまうと、
距離関数の値が0となってしまい、衝突座標からレイが進まなくなります。
この問題を回避するためのコードがcPos = q + normal * OFFSET;のOFFSETです。
normalはオブジェクト表面の法線で、この計算でレイの先端をオブジェクト表面から法線方向にOFFSETだけ移動させています。
この移動によって、距離関数の値がOFFSETとなり、反射後のレイ・マーチングができるようになります。
OFFSETという定数はEPSという定数の100倍に設定しました。
今回のマーチング・ループでは、距離関数の値が定数EPSより小さくなれば衝突したととみなしています。
100という数字には根拠はありませんが、EPSより十分に大きい値にする必要があります。
まとめ
駆け足気味になりましたが、この記事ではThree.jsからGPUをつかう方法とレイマーチングの原理について紹介した後に、レイマーチングの発展的なトピックとして特定のオブジェクトだけを色つける方法、鏡面反射させる方法を紹介しました。
レイマーチングを知らなかった方は「レイマーチングって面白そう!」と感じていただければ幸いです。
レイマーチングを既に知っていた方は、最後の発展的な話がお役に立てば幸いです。
2年くらい前に、大学のCG基礎という授業でC言語でレイトレーシングを実装しましたが、ソフトウェア実装だったので1フレームに描画するだけで数秒かかってしまいました。
今では、それがブラウザ上で、しかも携帯端末でもリアルタイムに動作するようになったと思うと、とても感慨深いなぁと思います。
おまけ
レイマーチングでは、CSG表現のようなオブジェクトの集合演算も得意とします。
鉄骨をモチーフとしたレイマーチングによる作品もつくったので紹介します。
上記のシーンを実現するための距離関数がこれです。
vec2 onRep(vec2 p, float interval) {
return mod(p, interval) - interval * 0.5;
}
float barDist(vec2 p, float interval, float width) {
return length(max(abs(onRep(p, interval)) - width, 0.0));
}
float tubeDist(vec2 p, float interval, float width) {
return length(onRep(p, interval)) - width;
}
float sceneDist(vec3 p) {
float bar_x = barDist(p.yz, 1.0, 0.1);
float bar_y = barDist(p.xz, 1.0, 0.1);
float bar_z = barDist(p.xy, 1.0, 0.1);
float tube_x = tubeDist(p.yz, 0.1, 0.025);
float tube_y = tubeDist(p.xz, 0.1, 0.025);
float tube_z = tubeDist(p.xy, 0.1, 0.025);
return max(max(max(min(min(bar_x, bar_y),bar_z), -tube_x), -tube_y), -tube_z);
}
一見すると複雑な形状のように見えますが、四角柱と円柱を組み合わせているだけなので、とてもシンプルです。
なんと20行に満たない距離関数で定義できました。