まずは挑戦してみよう
シェーダを自分でコーディングするなんて……
きっとお難しいんでしょ……
と、お思いの奥様方。そんなことはないんです。コツをつかめば意外と楽しめます。当連載では、シェーダというものに対して抱かれてしまいがちな、漠然とした 難しそう感 を払拭すべく、簡単なシェーダの記述とその基本について解説したいと思います。
前回:[連載]やってみれば超簡単! WebGL と GLSL で始める、はじめてのシェーダコーディング(9) - Qiita
想定する読者
当連載では、シェーダってなんか難しそう……とか、シェーダプログラミング始めてみたいけど……とか、なんとなく興味を持ってるけどシェーダを記述したことがない方を読者に想定しています。
たとえば Unity などのツール、あるいはマインクラフトのようなゲーム、またはモデリングソフトなどでもシェーダを自分で記述することができるような世の中です。きっとシェーダに触れた経験は無駄にはならないでしょう。
すぐに業務で活かすとか、そういう壮大な話はさておいてまずは気軽にシェーダに触れてみましょう。
難しい 3D の数学的知識はとりあえず要りません。もちろん難しいことをやろうとする場合は話が変わってきますが、当連載ではそのあたりの知識は求めません。ちょっとくらい、三角関数とかは出てきますがそんなに難しくないですから安心してください。
対象のシェーダ記述言語は GLSL
「シェーダ」という言葉には非常に広い意味が含まれるので、世の中にはシェーダといってもいろいろなものが存在しています。また、それを記述するための専用の言語にも、いくつか種類があったりして非常に初心者には敷居が高いのかなと思います。
当連載では GLSL というシェーダ専用言語を用います。
GLSL は 昨今話題の WebGL でも採用されているので、特別な開発環境の準備などをしなくても、ブラウザとテキストエディタさえあれば簡単に始められます。
また、当連載では著者自作の GLSL editor というオンラインでシェーダが記述できるエディタを使いますので、もはやブラウザとネット環境さえあればシェーダが書けます。気軽ですね。
それでは早速、前回に引き続き、シェーダプログラミングについて考えていきましょう。
組み合わせで生み出される映像
前回は GLSL 内で関数や定数、マクロなどを利用する方法について解説しました。
基本的な記述方法は C 言語などと比較的似ているので、すんなり理解できた人も多いのではないでしょうか。
さて、今回は長きにわたる GLSL チュートリアル連載の最終回です。
最終回は、今まで見てきた内容を踏まえつつ、あの大人気キャラクターをシェーダだけでレンダリングしてみましょう。
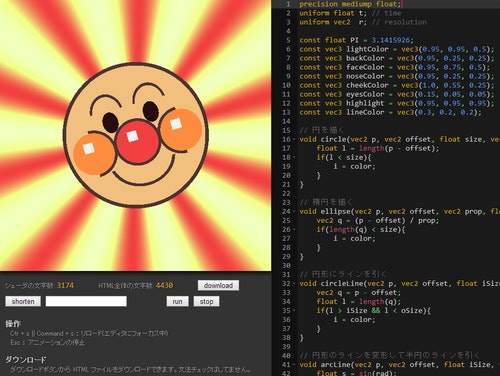
完成形はこんな感じになります。
一見すると、 こんなものがシェーダだけで描けるのか!? という不安に襲われるかもしれません。
しかし、心配することはありません。ここまで連載を読み進めてきたなら、きっとできます。この映像を映し出すためのテクニックは既に、ほとんどすべてが解説済み。要は応用と創意工夫だけで、これだけ複雑な映像を描きだすことができるはずです。
背景用のシェーダを作る
まず最初に、キャラクター本体よりも先に背景を作りましょう。
背景には、集中線のような模様を描き出します。
そのための簡易的なコードは次のようになります。
precision mediump float;
uniform float t; // time
uniform vec2 r; // resolution
const float PI = 3.1415926;
const vec3 lightColor = vec3(0.95, 0.95, 0.5); // 背景の後光の色
const vec3 backColor = vec3(0.95, 0.25, 0.25); // 背景の下地の色
// 背景の後光を描く
void sunrise(vec2 p, inout vec3 i){
float f = atan(p.y, p.x) + t;
float fs = sin(f * 10.0);
i = mix(lightColor, backColor, fs);
}
void main(){
// 座標を正規化する
vec2 p = (gl_FragCoord.xy * 2.0 - r) / min(r.x, r.y);
// 最終的に出力される色
vec3 destColor = vec3(1.0);
// 背景の後光を描く
sunrise(p, destColor);
gl_FragColor = vec4(destColor, 1.0);
}
冒頭から順に見ていきましょう。
まず最初に定数を使って、円周率や色の定義をしています。これらはシェーダ内では変化させないので、定数で十分ですね。
その下には、背景の模様を描くための関数を定義しました。sunrise 関数ですね。
この関数は、inout でデータを受け取り、上書きして返すタイプです。関数の中では、atan というアークタンジェントを計算するビルトイン関数や、mix という補間を行うためのビルトイン関数などが使われています。
この二つのビルトイン関数は今まで登場していないものですが、atan に関しては、まさにそのままアークタンジェントを計算してくれるだけです。
mix 関数は二つのベクトルを線形補間してくれます。第三引数に与えたパラメータによって、どのような比率で補間するのかが決まります。
今回の場合は、背景用の下地の色(明るめの赤)と、光の色(黄色)を、計算結果を係数として利用してミックスしてるわけですね。
キャラクター本体
さて、背景はできました。この上に前回の模様を描く関数たちを応用しながら呼び出しつつ、キャラクター本体を描いていきます。
少々長くなりますが、コードを一度全文掲載しておきますね。
precision mediump float;
uniform float t; // time
uniform vec2 r; // resolution
const float PI = 3.1415926;
const vec3 lightColor = vec3(0.95, 0.95, 0.5); // 背景の後光の色
const vec3 backColor = vec3(0.95, 0.25, 0.25); // 背景の下地の色
const vec3 faceColor = vec3(0.95, 0.75, 0.5); // 顔の色
const vec3 noseColor = vec3(0.95, 0.25, 0.25); // 鼻の色
const vec3 cheekColor = vec3(1.0, 0.55, 0.25); // 頬の色
const vec3 eyesColor = vec3(0.15, 0.05, 0.05); // 目の色
const vec3 highlight = vec3(0.95, 0.95, 0.95); // ハイライトの色
const vec3 lineColor = vec3(0.3, 0.2, 0.2); // ラインの色
// 円を描く
void circle(vec2 p, vec2 offset, float size, vec3 color, inout vec3 i){
float l = length(p - offset);
if(l < size){
i = color;
}
}
// 楕円を描く
void ellipse(vec2 p, vec2 offset, vec2 prop, float size, vec3 color, inout vec3 i){
vec2 q = (p - offset) / prop;
if(length(q) < size){
i = color;
}
}
// 円形にラインを引く
void circleLine(vec2 p, vec2 offset, float iSize, float oSize, vec3 color, inout vec3 i){
vec2 q = p - offset;
float l = length(q);
if(l > iSize && l < oSize){
i = color;
}
}
// 円形のラインを変形して半円のラインを引く
void arcLine(vec2 p, vec2 offset, float iSize, float oSize, float rad, float height, vec3 color, inout vec3 i){
float s = sin(rad);
float c = cos(rad);
vec2 q = (p - offset) * mat2(c, -s, s, c);
float l = length(q);
if(l > iSize && l < oSize && q.y > height){
i = color;
}
}
// 正方形を描く
void rect(vec2 p, vec2 offset, float size, vec3 color, inout vec3 i){
vec2 q = (p - offset) / size;
if(abs(q.x) < 1.0 && abs(q.y) < 1.0){
i = color;
}
}
// 背景の後光を描く
void sunrise(vec2 p, inout vec3 i){
float f = atan(p.y, p.x) + t;
float fs = sin(f * 10.0);
i = mix(lightColor, backColor, fs);
}
void main(){
// 座標を正規化する
vec2 p = (gl_FragCoord.xy * 2.0 - r) / min(r.x, r.y);
// 最終的に出力される色
vec3 destColor = vec3(1.0);
// 背景の後光を描く
sunrise(p, destColor);
// おおもとの座標を回転させる
float s = sin(sin(t * 2.0) * 0.75);
float c = cos(sin(t * 2.0));
vec2 q = p * mat2(c, -s, s, c);
// 顔のパーツを順番に描いていく
circle(q, vec2(0.0), 0.5, faceColor, destColor);
circle(q, vec2(0.0, -0.05), 0.15, noseColor, destColor);
circle(q, vec2(0.325, -0.05), 0.15, cheekColor, destColor);
circle(q, vec2(-0.325, -0.05), 0.15, cheekColor, destColor);
ellipse(q, vec2(0.15, 0.135), vec2(0.75, 1.0), 0.075, eyesColor, destColor);
ellipse(q, vec2(-0.15, 0.135), vec2(0.75, 1.0), 0.075, eyesColor, destColor);
circleLine(q, vec2(0.0), 0.5, 0.525, lineColor, destColor);
circleLine(q, vec2(0.0, -0.05), 0.15, 0.17, lineColor, destColor);
arcLine(q, vec2(0.325, -0.05), 0.15, 0.17, PI * 1.5, 0.0, lineColor, destColor);
arcLine(q, vec2(-0.325, -0.05), 0.15, 0.17, PI * 0.5, 0.0, lineColor, destColor);
arcLine(q * vec2(1.2, 1.0), vec2(0.19, 0.2), 0.125, 0.145, 0.0, 0.02, lineColor, destColor);
arcLine(q * vec2(1.2, 1.0), vec2(-0.19, 0.2), 0.125, 0.145, 0.0, 0.02, lineColor, destColor);
arcLine(q * vec2(0.9, 1.0), vec2(0.0, -0.15), 0.2, 0.22, PI, 0.055, lineColor, destColor);
rect(q, vec2(-0.025, 0.0), 0.035, highlight, destColor);
rect(q, vec2(-0.35, 0.0), 0.035, highlight, destColor);
rect(q, vec2(0.3, 0.0), 0.035, highlight, destColor);
gl_FragColor = vec4(destColor, 1.0);
}
前回も登場した関数のほか、いくつかの定数が追加されている状態です。
つい先ほど解説した、背景に後光を描くための関数も入っていますね。
circle と ellipse、それと rect に関しては前回も登場した関数ですね。今回は新たに circleLine と arcLine の二つを追加しました。でも、これらの追加のユーザー定義関数もやってることはあんまり変わりませんね。
ラインを引きたかったので上記の二つの関数を定義したのですが、仕組みは簡単です。
たとえば circleLine 関数のコードは次のようになっています。
// 円形にラインを引く
void circleLine(vec2 p, vec2 offset, float iSize, float oSize, vec3 color, inout vec3 i){
vec2 q = p - offset;
float l = length(q);
if(l > iSize && l < oSize){
i = color;
}
}
円形にラインを引くというと、いったいどんな計算をしたらいいのか想像しにくいかもしれません。しかし、仕組みは非常に簡単なんです。
要は、円をくり抜くようにして、半径が一定の範囲以下になる場合はなにもしなければいいんです。
イメージとしては、まず大きな円がある状態を想像してみてください。その中にひとまわり小さな円を置いて、小さな円の部分をくり抜いてしまうイメージです。結果的に、二つの円の半径を調整すれば、くり抜かれずに残った部分は線のように見えるわけですね。
この関数の第一引数は今までと同じように正規化済みの座標が入ります。第二引数は、描かれる位置のオフセットを表す vec2 型のデータ。この辺も、他の関数と同じですね。
第三引数の iSize には、ラインを引くための仮想的な小さい円の半径です。
第四引数の oSize が、ラインを引くための仮想的な大きいほうの円の半径ですね。
第五引数は条件に適合した場合に上塗りする色の指定。第六引数は inout が付いていることからもわかるとおり、参照で受け取る色データ格納用の変数ですね。
半円のライン
円形のラインの描き方がわかってしまえば、あとはそれを少しだけ応用すれば半円形のラインは引けます。
arcLine というユーザー定義関数は、そんな半円形のラインを引くことができる関数です。
中身で何をやっているのかは……
これはぜひ、自分で解明してみてください。
これまでに登場していないような、特殊な技術は何も使っていません。今までの応用だけで、必ず理解できるはずです。
終わりに
GLSL でシェーダを記述する……そんなふうに言われるととても難しいことをやるような気がします。
数学バリバリで、暗号のような記号の羅列が出てきそうなイメージさえあります。
しかし、当連載ではそんなイメージをどうにか払拭したくて、十回に渡って解説を行ってきました。
シェーダを自分で書くことができるようになるには、実のところ、基本的な数学の知識や、シェーダ言語に対する慣れが必要だと思っています。どちらも、一朝一夕では身に着くものではありませんが、数学の知識がそれほどなくても、シェーダを書くことはできるのです。
まずはやってみること。
そして興味が出たら、少しずつ勉強して知識を蓄積していくこと。
この繰り返しが大事だと思います。
今回の某キャラクターがレンダリングされるシェーダは、以下のリンクから実際に動くものを見ることができます。
また、2014年の 11月末 12月末あたりまでの期間でこんな企画もやっています。
ぜひ、気軽に参加してください。
みんなで楽しいシェーダライフを満喫しましょう!
最後までお読みいただいて、ありがとうございました。