まずは挑戦してみよう
シェーダを自分でコーディングするなんて……
きっとお難しいんでしょ……
と、お思いの奥様方。そんなことはないんです。コツをつかめば意外と楽しめます。当連載では、シェーダというものに対して抱かれてしまいがちな、漠然とした 難しそう感 を払拭すべく、簡単なシェーダの記述とその基本について解説したいと思います。
前回:[連載]やってみれば超簡単! WebGL と GLSL で始める、はじめてのシェーダコーディング(8) - Qiita
想定する読者
当連載では、シェーダってなんか難しそう……とか、シェーダプログラミング始めてみたいけど……とか、なんとなく興味を持ってるけどシェーダを記述したことがない方を読者に想定しています。
たとえば Unity などのツール、あるいはマインクラフトのようなゲーム、またはモデリングソフトなどでもシェーダを自分で記述することができるような世の中です。きっとシェーダに触れた経験は無駄にはならないでしょう。
すぐに業務で活かすとか、そういう壮大な話はさておいてまずは気軽にシェーダに触れてみましょう。
難しい 3D の数学的知識はとりあえず要りません。もちろん難しいことをやろうとする場合は話が変わってきますが、当連載ではそのあたりの知識は求めません。ちょっとくらい、三角関数とかは出てきますがそんなに難しくないですから安心してください。
対象のシェーダ記述言語は GLSL
「シェーダ」という言葉には非常に広い意味が含まれるので、世の中にはシェーダといってもいろいろなものが存在しています。また、それを記述するための専用の言語にも、いくつか種類があったりして非常に初心者には敷居が高いのかなと思います。
当連載では GLSL というシェーダ専用言語を用います。
GLSL は 昨今話題の WebGL でも採用されているので、特別な開発環境の準備などをしなくても、ブラウザとテキストエディタさえあれば簡単に始められます。
また、当連載では著者自作の GLSL editor というオンラインでシェーダが記述できるエディタを使いますので、もはやブラウザとネット環境さえあればシェーダが書けます。気軽ですね。
それでは早速、前回に引き続き、シェーダプログラミングについて考えていきましょう。
関数の定義と呼び出し
前回は行列を用いて座標を回転させる方法について解説しました。
このような簡単な行列の扱い方を覚えておくと、様々な面で応用が利きます。特に二次元の座標を回転させるだけなら暗記してしまえるレベルなので、覚えておくといいかもしれません。
さて、当連載も早いもので今回で第九回。
シェーダのコードも徐々に長くなってきて、順番に読み進めてきている方でないと内容がわかりにくくなってきたころではないかと思います。
今回は、シェーダのコードをうまく整理するのには欠かせない 関数の定義方法 から見ていきます。しかし、いわゆる C 言語や javascript と基本的にはほとんど同じなので、簡単だと思います。
GLSL における関数の記述の注意点としては、まず第一に記述の順序があります。
関数は、必ず利用される(呼び出される)前の段階で定義が済んでいなければなりません。
vec3 myFunction(){
return vec3(0.0);
}
void main(){
vec3 v = myFunction();
}
上記の例では、main 関数の中でユーザー定義の関数を呼びだしていますが、main 関数の記述よりも前に(コードの位置で言うと先に)書かれているので、問題は起こりません。逆に、次のようにしてしまうとエラーが出てしまいます。
vec3 myFunction(){
return myFunction2();
}
void main(){
vec3 v = myFunction();
}
vec3 myFunction2(){
return vec3(1.0);
}
この場合、正しく動くようにするためには、コードの最上段に myFunction2 を記述しておく必要があります。
要は、記述する順序に気を付ければいいわけですね。
戻り値と引数
関数と言えば戻り値と引数についてもしっかり理解しておくことが大事です。
何も戻り値のない関数の場合、main 関数と同じように戻り値の型は void として記述しておきましょう。
void myFunction(){
// 何かしらの処理
}
引数にデータを受け取るような構造にする場合には、型名と変数名を記述します。
これはほとんど見たまんまですので簡単だと思います。
void myFunction(vec3 position, vec2 texCoord){
// 何かしらの処理
}
さらに、少々特殊な書き方として、in や out、inout などを利用して、関数内での読み出し専用や書き出し専用などの指定をすることもできます。
イメージとしては参照渡しですね。
void myFunction(inout float arg){
arg *= 0.5;
}
void main(){
float f = 1.0;
myFunction(f);
gl_FragColor = vec4(vec3(f), 1.0);
}
上記のようにすれば、main 関数のほうで定義している変数 f が動的に書き換えられ、結果的に出力結果はグレーに塗りつぶされた状態になります。
この inout を利用した記述方法は、これができることによって何が便利なのかイメージしにくいかもしれません。実際のところ、これを使ったほうが都合がいい場面は、それなりに複雑なことをしようとする場合だけだと思います。無理に使わなくても記述できるなら、それはそれで構わないでしょう。
仮に使うようなケースがあるとすれば、たとえば複数の異なる関数を連続して呼び出していく際に、関数の結果をどんどん継承して引数に渡していきたいような場合でしょうか。
通常は、戻り値を返して事足りる場合がほとんどだと思いますし、それで慣れてしまってまったく問題ありません。
以下のように書けば、先ほどとやっていることはまったく同じ意味になりますね。
float myFunction(float arg){
return arg * 0.5;
}
void main(){
float f = 1.0;
float g = myFunction(f);
gl_FragColor = vec4(vec3(g), 1.0);
}
定数やマクロ
GLSL では 定数 を用いることも可能です。
定数は GLSL のなかで値が不変のものに利用します。いわゆる一般的な定数と同じですね。定数はシェーダ内で最適化されるので、通常の変数を用いる場合と比べて若干パフォーマンスがいいらしいです。
定数を定義するには const を用いて以下のように記述します。
const vec3 POSITION = vec3(0.0);
定数を用いる場合は、適宜大文字による記述にするなど工夫すると、通常の変数と見分けがつきやすくなりますね。
また、GLSL では define マクロを利用することもできます。
define マクロは文の初めに # を加えて記述します。また、文末にセミコロンは要らないので注意しましょう。
# define white vec4(1.0)
上記のように書くと、GLSL 内で white と記述した箇所には vec4(1.0) がマクロによって埋め込まれます。
一見すると、定数とマクロは非常に役割が似ていますね。しかし、定数はあくまでも値が不変の変数のように振る舞うのに対して、マクロは動的にコードの内容をそのまま書き換えます。
ですから、たとえば次のようなこともマクロなら可能です。
# define f float
f varFloat = 1.0;
本来であれば、f なんていう変数の型は存在しませんが、マクロによってコードが書きかえられることで、f と記述されたところには float という単語が埋め込まれ、結果的にエラーが起こらなくなるのですね。このような書き方は定数では行うことができません。
両者の違いを理解しつつ、うまく活用していきましょう。
実際に使ってみよう
さて、それでは上記で解説してきた技術を使って、単純な図形を描き出す関数を作ってみましょう。
円や、楕円、あるいは四角形、こういった基本的な図形を描き出す GLSL の関数を定義してみます。
まずは、完成形のコード全文を見てみましょう。
precision mediump float;
uniform float t; // time
uniform vec2 r; // resolution
# define white vec3(1.0)
const vec3 red = vec3(1.0, 0.0, 0.0);
const vec3 green = vec3(0.0, 1.0, 0.0);
const vec3 blue = vec3(0.0, 0.0, 1.0);
void circle(vec2 p, vec2 offset, float size, vec3 color, inout vec3 i){
float l = length(p - offset);
if(l < size){
i = color;
}
}
void rect(vec2 p, vec2 offset, float size, vec3 color, inout vec3 i){
vec2 q = (p - offset) / size;
if(abs(q.x) < 1.0 && abs(q.y) < 1.0){
i = color;
}
}
void ellipse(vec2 p, vec2 offset, vec2 prop, float size, vec3 color, inout vec3 i){
vec2 q = (p - offset) / prop;
if(length(q) < size){
i = color;
}
}
void main(void){
vec3 destColor = white;
vec2 p = (gl_FragCoord.xy * 2.0 - r) / min(r.x, r.y);
circle (p, vec2( 0.0, 0.5), 0.25, red, destColor);
rect (p, vec2( 0.5, -0.5), 0.25, green, destColor);
ellipse(p, vec2(-0.5, -0.5), vec2(0.5, 1.0), 0.25, blue, destColor);
gl_FragColor = vec4(destColor, 1.0);
}
結構長いですね。
でも、ポイントを押さえていけばそれほど難しくないと思います。
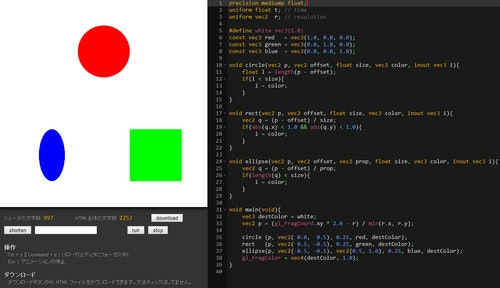
ちなみに、これを実行した結果がどうなるのかというと……
結構地味です(笑)
こんな感じですね。
では一番簡単な円を描く関数から見ていきます。
void circle(vec2 p, vec2 offset, float size, vec3 color, inout vec3 i){
float l = length(p - offset);
if(l < size){
i = color;
}
}
まず、最初にポイントとなるのが、この関数は 戻り値を返さない ということです。
よく見るとわかると思いますが、戻り値の型には void が指定されていますね。このことから、この関数が戻り値を返さないことがわかると思います。
しかし一方で、いくつかある引数のうち、一番最後に注目してみてください。
inout を利用した引数の指定をしていますね。
これは先ほども書いたように、引数として受け取った変数を動的に書き換えて返却できる宣言の仕方です。つまり、この関数は戻り値を返すのではなく、引数として受け取った変数を動的に書き換える仕様になっているというわけですね。
呼び出すときは、次のようにして呼び出します。
void main(void){
vec3 destColor = white;
vec2 p = (gl_FragCoord.xy * 2.0 - r) / min(r.x, r.y);
circle (p,vec2(0.0, 0.5), 0.25, vec3(0.0), destColor);
gl_FragColor = vec4(destColor, 1.0);
}
第一引数には、正規化済みの座標を渡します。第二引数には、円を描く座標を移動させたい場合に、オフセットさせる移動量を vec2 型で与えます。
第三引数は、円の大きさ、つまり半径ですね。上記の例だと、半径が 0.25 の円が描かれることになります。
第四引数は円に塗る色の指定を RGB で入れます。そして最後の第五引数が、関数の中で動的に書き換えられることになる、参照される変数になります。
このようにして呼び出された関数の、その中ではどんなことが起こるのでしょうか。
void circle(vec2 p, vec2 offset, float size, vec3 color, inout vec3 i){
float l = length(p - offset);
if(l < size){
i = color;
}
}
circle 関数の中では、length を利用してベクトルの長さを測っていますね。そして、この長さが、引数として入ってくる円の半径以下だった場合には、指定された色で inout 変数を上書きするようになっています。
以前の連載テキストで length 関数などの意味をしっかり理解できていれば、この circle 関数の中身自体はそれほど難しくないと思います。要は、ベクトルの大きさを調べて、指定された半径よりも小さいベクトルだった場合だけ、色の上塗りをするのですね。
その他の図形関数
円の場合と同様の仕組みを使って、その他の図形関数も実装されています。
inout 指定された変数を、特定の条件に当てはまるときだけ上書きするような構造はいずれの関数でも共通です。
矩形、つまり四角形を描く関数は以下のような感じになっています。
void rect(vec2 p, vec2 offset, float size, vec3 color, inout vec3 i){
vec2 q = (p - offset) / size;
if(abs(q.x) < 1.0 && abs(q.y) < 1.0){
i = color;
}
}
正規化済みの座標、移動量を示す vec2、矩形の大きさ、上塗りする色など、どれも同じですね。
関数の中では、指定されたサイズで座標を除算するような処理が入っていますね。
今まで、光の表現の多くで見てきたように、除算を行う場合には 割る数が小さくなるほど結果は大きくなる のでしたね。仮に、引数 size に 0.5 が指定されていたとすると、0.5 で割る処理が発生して結果的に座標は 2 倍の大きさになります。
ちょっとわかりにくいかもしれませんが、落ち着いて考えてみてくださいね。
size による除算が行われた後の座標系を使って、if 文による判定をしてあげると矩形領域として塗りつぶしてやるべきかどうかが定まります。今回の場合は、サイズの指定が float なので矩形は全部正方形になりますね。
もし vec2 などのデータ型でサイズを指定するようにすれば、長方形でも自在に描くことができるように改造できるでしょう。
そして、今矩形の関数でやったのと同じような計算をすると、円を歪ませて楕円形に加工することもできます。
それを実際にやっているのが楕円を描く ellipse 関数ですね。
void ellipse(vec2 p, vec2 offset, vec2 prop, float size, vec3 color, inout vec3 i){
vec2 q = (p - offset) / prop;
if(length(q) < size){
i = color;
}
}
これを見るとわかるとおり、矩形の場合と同じように冒頭で除算処理が行われています。
これも、注意深く式を見てみれば、比較的簡単だと思います。
わかりやすく記述する
定数やマクロ、あるいは関数といった技術は、自分自身がわかりやすいように利用するように心がけましょう。
今回紹介した技術は、いずれも利用しなくても GLSL は記述できますし、逆に言えば無理矢理使う必要はまったくないものばかりです。
それらを利用することによって、よりコードがわかりやすくなったり、あるいは記述しやすくなったりします。使い方を誤って、むしろ混乱を招いてしまうようでは本末転倒です。
自分がイメージしやすい名前を付けて、混乱してしまわないように気を付けましょう。
今回紹介した関数は、基本的な図形を描くだけなのであまり面白味がありませんでしたね。しかし、これを工夫してやることで、驚くような映像を生み出すこともできるんです。要は、創意工夫が大切です。
次回は、今回のような基本的な図形を組み合わせて、もう少し絵になるものをスクリーンに描いてみましょう。
お楽しみに!
次回:[連載]やってみれば超簡単! WebGL と GLSL で始める、はじめてのシェーダコーディング(最終回) - Qiita