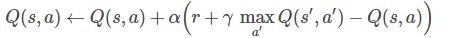DQNで自作迷路を解く
Deep Q Network(いわゆるDQN)で自作の迷路を解いてみました。
プログラムはこちらにあります。
https://github.com/shibuiwilliam/maze_solver
概要
DQNは強化学習の一種で、最適な戦略選択にニューラルネットワークを使っているものになります。
強化学習やニューラルネットワークの説明は以下が参考になります。
- 強化学習
ゼロからDeepまで学ぶ強化学習 - Qiita - ニューラルネットワーク
TensorFlowのチュートリアルを通して、人工知能の原理について学習する - Qiita
強化学習はゲームやロボット制御で使われている技術なのですが、状況(State)に対してプレイヤー(エージェントとも)が行動(Action)を起こすことで、状況の変化とその行動への報酬(reward)を得るモデルです。
状況に対する行動を繰り返すことプレイヤーは報酬の最大化を目指します。
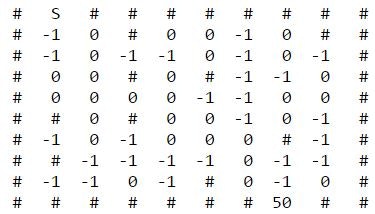
今回は状況に自作の迷路を使います。
迷路はプログラムで自動生成していますが、こういうイメージのものです。
10×10でSがスタート地点、50がゴールです。
周囲を壁(#)で囲まれており、内部の数字が書いてあるタイル(-1、0)のみ通れます。
壁の内部でも#になっているタイルは通れません。
タイルの数字はポイント(強化学習的にいうと報酬)です。
-1は1点マイナス、0点は変化なし、ゴールは50点獲得です。
プレイヤーはポイントを最大化してゴールすることを目指します。
プレイヤーがゴールへ至るロジックとして、今回は以下3つを実装しました。
- A-starアルゴリズム
- Q-Learning
- Deep Q-network(DQN)
それぞれの概要は以下です。
A-starアルゴリズム
A-starアルゴリズムはここの説明がとてもわかりやすいです。
pythonで迷路探索するよ<解答解説編> - すこしふしぎ.
A* - Wikipedia
単純化して言うと、スタート地点から現在地、そして現在地からゴールまでの距離を計測し、距離が最短になるルートを選んでいくというものです。
迷路では各距離はユークリッド距離で計算します。
$$
距離^2 = (goal[x] - state[x])^2 + (goal[y] - state[y])^2
$$
ピタゴラスの定理(三平方の定理)に出てくる式ですね。
A-starアルゴリズムを使うと最短距離を優先して迷路を解いていきます。
ポイントや報酬という概念はありません。
ですので、今回のルールの迷路だと、迷路を速く解く一方で報酬が低い傾向にあります。
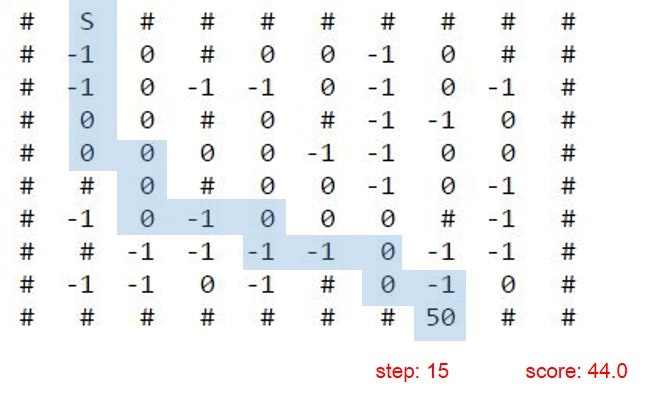
A-starで解いたときのスタートからゴールまでの道のりがこちらです。
通ったルートは青色にしています。
今回使った迷路でも最短距離をいきますが、報酬は低く44点です。-1でもなんでも、最短距離を目指します。
Q-learning
続いてQ学習です。
Q学習 - Wikipedia
Pythonではじめる強化学習 - Qiita
Q学習は迷路探索以外にも使える汎用的な手法です。
機械学習の一種で、状況と自分の行動を学習データにして、その報酬をターゲット変数にしてモデルを作っていきます。
状況に応じて行った行動に対する報酬を予測モデルを作るのです。
報酬の予測は以下のような式で計算します。
$Q(s,a)$は状況$s$で行動$a$を行ったときの報酬の期待値です。
$α$は学習率、$γ$は報酬の割引率です。
$Q(s', a')$は状況$s$の次の状況$s'$で行動$a'$を行ったときの報酬の期待値です。
$max$で期待値$Q(s', a')$の最大値をとり、割引率$γ$をかけます。
$r$は状況$s$で行動$a$を行ったときの報酬です。
Q学習の特徴はこの式を繰り返し計算することで、報酬の見込値$Q(s,a)$と期待値$r+γmaxQ(s',a')$を近づけていく(結果として$Q(s,a)←Q(s,a)+0$に収斂していく)ことにあります。
Q学習ではまず、充分大きな回数の繰り返しで状態、行動、報酬の組み合わせを取得していきます。
これを入力にして上記の式を繰り返し計算していき、実態にあった報酬の期待値$Q(s,a)$を導き出そうといういものです。
Q学習は報酬の最大化を目指します。
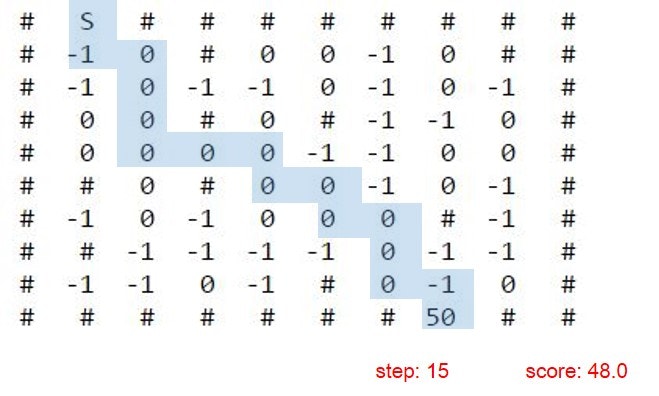
今回の迷路ではゴールを最大の報酬にしておりますので、Q学習で迷路を解くと、-1のタイルを回避しながら迅速にゴールに向かって行きます。
その様子がこちらです。
可能な限り0のタイルを通りながら最短距離でゴールしています。
報酬も48.0と、A-starより高得点です。
DQN
DQNはQ学習にディープラーニングを組み合わせたものです。
状況$s$、行動$a$を入力変数とし、Q学習に出てきた$r+γmaxQ(s',a')$をターゲット変数としたニューラルネットワークを構築します。
$s$、$a$から$r+γmaxQ(s',a')$を近似し誤差を最小化していくことで、状態$s$に対して報酬$r$を最大化する行動$a$を導き出していくものになります。
DQNが通常のニューラルネットワークと違うのは、プログラムが教師あり学習の教師データを生成していく点です。
ニューラルネットワークの学習には教師データが必要ですが、DQNでは状態$s$に対する行動$a$とその報酬$r$を、実際に行動することで溜め込んでいきます
入力変数、ターゲット変数は行動を繰り返すことで$s$,$a$,$r$の組み合わせを記録しておき、一定以上溜まったメモリを元に学習を行います。
Experience Replayというのですが、自ら記録した$s$,$a$,$r$の組み合わせからサンプリングしたもので学習し予測モデルをつくって、また行動を繰り返して$s$,$a$,$r$の組み合わせを得て予測モデルを修正する、という流れをとります。
こちらがExperience Replayを提唱している論文です。
https://pdfs.semanticscholar.org/9cd8/193a66cf53143cbba6ccb0c7b9c2ebf2452b.pdf
日本語だとこちらの説明がわかりやすいです。
DQNの生い立ち + Deep Q-NetworkをChainerで書いた - Qiita
一部引用します:
input: 多数のサンプル($s$, $a$, $r$, $s'$)からなるデータ $D$
output: 学習後のQ関数 $Q_{\theta_N} (s,a)$
- $k=0$
- ニューラルネットワークのパラメータ $\theta_0$ を初期化する
- 繰り返し: $N-1$ 回繰り返す
- データ $D$ からサンプルを $M$ 個取り出す
5. $M$個のサンプルを元に、
教師信号 $ {\rm{target}}^t = r_t + \gamma \max_{a'} Q_{\theta_k} (s_t',a') $ と
入力 $ (s_t, a_t) $ を作成する( $t=1,2,...,M$ )
6. 作成した教師信号 ${\rm{target}}^t$ と入力$ (s_t, a_t) $を元に、
$Q_\theta (s, a)$ と教師信号との誤差$L_\theta$ を何らかの勾配法で最小化
する。学習が収束するなり一定の条件を満たしたら、その結果を
$\theta_{k+1}$とする
7. $k \leftarrow k+1$とする - $Q_{\theta_N} (s,a)$ を返す
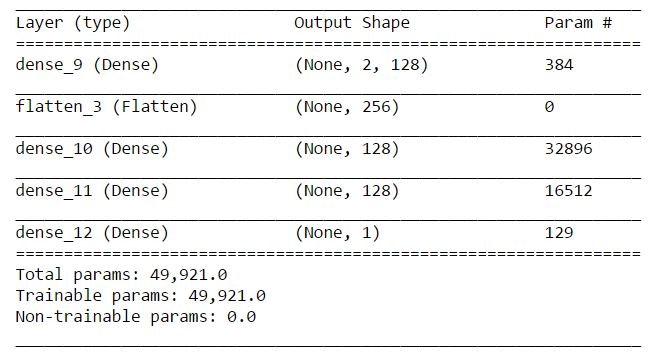
ニューラルネットワークはKerasで書いています。
モデルはこんな感じです。
DQNだけプログラムを載せます。
プログラム全文はこちらです。
https://github.com/shibuiwilliam/maze_solver
以下がエージェントです。
ニューラルネットワークモデル、状態・行動・報酬を格納するメモリ、行動選択、Experience Replayで構成されています。
クラス変数のepsilonはランダムな行動をとる確率です。
この値はトレーニングを進める毎にe_decayで減衰していきます。
e_minがepsilonの最小値です。
最終的には予測モデルに従って最適な行動を取るようになりますが、はじめのうちはランダムに行動してサンプリングします。
class DQN_Solver:
def __init__(self, state_size, action_size):
self.state_size = state_size # list size of state
self.action_size = action_size # list size of action
self.memory = deque(maxlen=100000) # memory space
self.gamma = 0.9 # discount rate
self.epsilon = 1.0 # randomness of choosing random action or the best one
self.e_decay = 0.9999 # epsilon decay rate
self.e_min = 0.01 # minimum rate of epsilon
self.learning_rate = 0.0001 # learning rate of neural network
self.model = self.build_model() # model
self.model.summary() # model summary
# model for neural network
def build_model(self):
model = Sequential()
model.add(Dense(128, input_shape=(2,2), activation='tanh'))
model.add(Flatten())
model.add(Dense(128, activation='tanh'))
model.add(Dense(128, activation='tanh'))
model.add(Dense(1, activation='linear'))
model.compile(loss="mse", optimizer=RMSprop(lr=self.learning_rate))
return model
# remember state, action, its reward, next state and next possible action. done means boolean for goal
def remember_memory(self, state, action, reward, next_state, next_movables, done):
self.memory.append((state, action, reward, next_state, next_movables, done))
# choosing action depending on epsilon
def choose_action(self, state, movables):
if self.epsilon >= random.random():
# randomly choosing action
return random.choice(movables)
else:
# choosing the best action from model.predict()
return self.choose_best_action(state, movables)
# choose the best action to maximize reward expectation
def choose_best_action(self, state, movables):
best_actions = []
max_act_value = -100
for a in movables:
np_action = np.array([[state, a]])
act_value = self.model.predict(np_action)
if act_value > max_act_value:
best_actions = [a,]
max_act_value = act_value
elif act_value == max_act_value:
best_actions.append(a)
return random.choice(best_actions)
# this experience replay is going to train the model from memorized states, actions and rewards
def replay_experience(self, batch_size):
batch_size = min(batch_size, len(self.memory))
minibatch = random.sample(self.memory, batch_size)
X = []
Y = []
for i in range(batch_size):
state, action, reward, next_state, next_movables, done = minibatch[i]
input_action = [state, action]
if done:
target_f = reward
else:
next_rewards = []
for i in next_movables:
np_next_s_a = np.array([[next_state, i]])
next_rewards.append(self.model.predict(np_next_s_a))
np_n_r_max = np.amax(np.array(next_rewards))
target_f = reward + self.gamma * np_n_r_max
X.append(input_action)
Y.append(target_f)
np_X = np.array(X)
np_Y = np.array([Y]).T
self.model.fit(np_X, np_Y, epochs=1, verbose=0)
if self.epsilon > self.e_min:
self.epsilon *= self.e_decay
Experience Replayでは現在の状態、行動、報酬とその次の状態、最適な行動、報酬をニューラルネットワークに渡して学習しています。
現在の行動に対する期待値を近似します。
こちらがモデルのトレーニングです。
episodesがトレーニングを行う回数で、timesが1 episodeにおけるサンプリング(探索)の回数です。
サンプリング→トレーニングを1000×20000回繰り返しています。
ただし、サンプリング途中でゴールしたら、そのサンプリングは中断します。
サンプリングとトレーニングの回数はepsilonとe_decayの値と合わせて調整します。
サンプリング(times)が少ないとExperience Replayできるサンプルデータが足りませんし、トレーニング回数(episodes)が少ないとニューラルネットワークがモデルを学習しません。
epsilon値はepisodes毎に減衰しているので、この値がe_decayに従って充分に小さい値にならないと、どんなに良いモデルがあっても、サンプリング中はランダムな行動をとり続け、モデルを評価できません。
この辺の値は迷路のサイズによって調整します。
10×10であれば今回の数値でモデルが生成できましたが、サイズが大きいとサンプリング回数が足りていないうちにトレーニングが終了してしまい、偏ったモデルができあがります。
# train the model
state_size = 2
action_size = 2
dql_solver = DQN_Solver(state_size, action_size)
# number of episodes to run training
episodes = 20000
# number of times to sample the combination of state, action and reward
times = 1000
for e in range(episodes):
state = start_point
score = 0
for time in range(times):
movables = maze_field.get_actions(state)
action = dql_solver.choose_action(state, movables)
reward, done = maze_field.get_val(action)
score = score + reward
next_state = action
next_movables = maze_field.get_actions(next_state)
dql_solver.remember_memory(state, action, reward, next_state, next_movables, done)
if done or time == (times - 1):
if e % 500 == 0:
print("episode: {}/{}, score: {}, e: {:.2} \t @ {}"
.format(e, episodes, score, dql_solver.epsilon, time))
break
state = next_state
# run experience replay after sampling the state, action and reward for defined times
dql_solver.replay_experience(32)
以下はトレーニングの実行結果です。
500エピソード毎に出力しています。
scoreがそのエピソードの報酬、eがepsilon、@がサンプリング回数です。
@が少ないということは、サンプリング途中でゴールしているということです。
episode: 0/20000, score: 5.0, e: 1.0 @ 100
episode: 500/20000, score: 19.0, e: 0.95 @ 86
episode: 1000/20000, score: 14.0, e: 0.9 @ 82
episode: 1500/20000, score: 24.0, e: 0.86 @ 56
episode: 2000/20000, score: -9.0, e: 0.82 @ 138
episode: 2500/20000, score: 26.0, e: 0.78 @ 76
episode: 3000/20000, score: 20.0, e: 0.74 @ 84
episode: 3500/20000, score: 42.0, e: 0.7 @ 24
episode: 4000/20000, score: 44.0, e: 0.67 @ 22
episode: 4500/20000, score: 45.0, e: 0.64 @ 24
episode: 5000/20000, score: 46.0, e: 0.61 @ 36
episode: 5500/20000, score: 33.0, e: 0.58 @ 32
episode: 6000/20000, score: 43.0, e: 0.55 @ 32
episode: 6500/20000, score: 48.0, e: 0.52 @ 24
episode: 7000/20000, score: 38.0, e: 0.5 @ 34
episode: 7500/20000, score: 45.0, e: 0.47 @ 28
episode: 8000/20000, score: 43.0, e: 0.45 @ 42
episode: 8500/20000, score: 43.0, e: 0.43 @ 24
episode: 9000/20000, score: 45.0, e: 0.41 @ 28
episode: 9500/20000, score: 45.0, e: 0.39 @ 28
episode: 10000/20000, score: 48.0, e: 0.37 @ 20
episode: 10500/20000, score: 44.0, e: 0.35 @ 22
episode: 11000/20000, score: 46.0, e: 0.33 @ 24
episode: 11500/20000, score: 45.0, e: 0.32 @ 22
episode: 12000/20000, score: 48.0, e: 0.3 @ 26
episode: 12500/20000, score: 45.0, e: 0.29 @ 18
episode: 13000/20000, score: 47.0, e: 0.27 @ 18
episode: 13500/20000, score: 41.0, e: 0.26 @ 24
episode: 14000/20000, score: 47.0, e: 0.25 @ 16
episode: 14500/20000, score: 47.0, e: 0.23 @ 14
episode: 15000/20000, score: 47.0, e: 0.22 @ 14
episode: 15500/20000, score: 48.0, e: 0.21 @ 14
episode: 16000/20000, score: 46.0, e: 0.2 @ 18
episode: 16500/20000, score: 44.0, e: 0.19 @ 20
episode: 17000/20000, score: 48.0, e: 0.18 @ 14
episode: 17500/20000, score: 45.0, e: 0.17 @ 20
episode: 18000/20000, score: 48.0, e: 0.17 @ 18
episode: 18500/20000, score: 48.0, e: 0.16 @ 20
episode: 19000/20000, score: 46.0, e: 0.15 @ 18
episode: 19500/20000, score: 48.0, e: 0.14 @ 16
エピソードを繰り返すとスコアが上昇し、epsilonが減衰し、サンプリング回数が減少していきます。
良いモデルに集約していっているのがわかります。
作ったモデルで迷路を解いてみます。
# try the model
state = start_point
score = 0
steps = 0
while True:
steps += 1
movables = maze_field.get_actions(state)
action = dql_solver.choose_best_action(state, movables)
print("current state: {0} -> action: {1} ".format(state, action))
reward, done = maze_field.get_val(action)
maze_field.display(state)
score = score + reward
state = action
print("current step: {0} \t score: {1}\n".format(steps, score))
if done:
maze_field.display(action)
print("goal!")
break
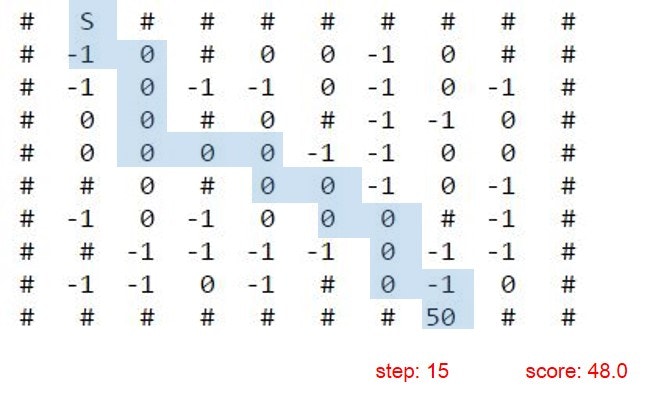
結果はQ学習と同じなりました。
両者で求めているものは同じですし、このサイズの迷路ではさもありなんでしょう。
おわりに
DQNを触ってみたくて、ついでに迷路探索のアルゴリズムを比較してみました。
うまいことDQNが動いて楽しかったです。
一番苦労したのはいずれのアルゴリズムでも使える迷路プログラムを書くことですが、今でもときどき解けない迷路(ゴールが壁で阻まれていたり)ができたりしますが、疲れたので修正は後回しにしました。
あと、DQNのパラメータ調整は時間がかかりますね。
今20×20の迷路で検証しているので、これが完了したらまたアップロードします。