今回はPRML実装一回目の終わりで少し言及したエビデンス近似を実装しました。この手法は、他にも経験ベイズ、第二種の最尤推定などとも呼ばれています。機械学習のアルゴリズムを使用していると超パラメータを設定しないといけないことが多々あります。この手法を使うことで今までなんとなく決めていた超パラメータをデータから自動的に決めてくれます。
ベイズ線形回帰
エビデンス近似の説明に入る前にベイズ線形回帰の説明をします。
最尤推定
トレーニングデータ$\{x_i, t_i\}_{i=1}^N$が与えられたときに、特徴ベクトル${\bf\phi}$を用意して(例えば${\bf\phi}(x)=(1, x, x^2, x^3)^{\rm T}$)
{\bf t} =
\begin{bmatrix}
t_1\\
t_2\\
\vdots\\
t_N
\end{bmatrix}\\
{\bf\Phi} =
\begin{bmatrix}
\phi_1(x_1) & \phi_2(x_1) & \cdots & \phi_M(x_1)\\\
\phi_1(x_2) & \phi_2(x_2) & \cdots & \phi_M(x_2)\\\
\vdots & \vdots & \ddots & \vdots\\\
\phi_1(x_N) & \phi_2(x_N) & \cdots & \phi_M(x_N)
\end{bmatrix}\\
{\bf w} =
\begin{bmatrix}
w_1\\
w_2\\
\vdots\\
w_M
\end{bmatrix}\\
として、以下の尤度関数をパラメータ${\bf w}$について最小化します。ただし、${\bf I}$は$N\times N$の単位行列、$\beta$は精度パラメータとしています。
E({\bf w}) = \mathcal{N}({\bf t}|{\bf\Phi}{\bf w}, \beta^{-1}{\bf I})
事後分布
最尤推定ではトレーニングデータに過学習するかもしれないということでパラメータ${\bf w}$に事前分布を設定します。ということで平均0、分散$\alpha^{-1}$のガウス分布を事前分布とすると、ベイズの定理を用いて
\begin{align}
p({\bf w}|{\bf\Phi},{\bf t}, \alpha, \beta) &= {\mathcal{N}({\bf t}|{\bf\Phi}{\bf w}, \beta^{-1}{\bf I}) \mathcal{N}({\bf w}|{\bf 0}, \alpha^{-1}{\bf I})\over p({\bf t}|{\bf\Phi}, \alpha, \beta)}\\
&= \mathcal{N}({\bf w}|{\bf m}_N, {\bf S}_N)
\end{align}
として、パラメータ${\bf w}$についての事後分布が得られます。ただし、
{\bf m}_N = \beta {\bf S}_N{\bf\Phi}^{\rm T}{\bf t}\\
{\bf S}_N^{-1} = \alpha{\bf I} + \beta{\bf\Phi}^{\rm T}{\bf\Phi}
事後予測分布
上で求めた事後分布を使って、新たな入力$x$に対する$t$の事後予測分布は
p(t|x,{\bf\Phi},{\bf t},\alpha,\beta) = \int \mathcal{N}(t|{\bf w}^{\rm T}{\bf\phi}(x), \beta^{-1}) \mathcal{N}({\bf w}|{\bf m}_N, {\bf S}_N) {\rm d}{\bf w}\\
= \mathcal{N}(t|{\bf m}_N^{\rm T}{\bf\phi}(x), \sigma^2_N(x))
のようにパラメータ${\bf w}$について積分消去することで求まります。ただし、その分散は
\sigma^2_N(x) = {1\over\beta} + \phi(x)^{\rm T}{\bf S}_N\phi(x)
このようにして求めた事後予測分布を使うことでベイズ線形回帰ができました。この回帰の挙動は超パラメータ$\alpha,\beta$に依存する形となっています。もし、私たちが設定した超パラメータの値が大きすぎたり、小さすぎたりした場合、回帰の結果は望んだようにはならないかもしれません。
エビデンス近似
上では超パラメータ$\alpha,\beta$を人間が決めたなんらかの値としていましたが、これらをデータから推定します。パラメータ${\bf w}$の事後分布を求めるときに
p({\bf w}|{\bf\Phi},{\bf t}, \alpha, \beta) = {\mathcal{N}({\bf t}|{\bf\Phi}{\bf w}, \beta^{-1}{\bf I}) \mathcal{N}({\bf w}|{\bf 0}, \alpha^{-1}{\bf I})\over p({\bf t}|{\bf\Phi}, \alpha, \beta)}
としてベイズの定理を使いました。事後分布を求める場合、往々にして右辺の分子の部分にだけ着目しますが、実は分母の$p({\bf t}|{\bf\Phi},\alpha,\beta)$がエビデンス関数と呼ばれるものになっていて、以下のような関係になっています。
(尤度関数)\times(事前分布)=(エビデンス関数)\times(事後分布)
エビデンス関数の持つ意味を$p({\bf t}|{\bf\Phi},\alpha,\beta)$から考えると、エビデンス関数は、与えられた超パラメータ$\alpha,\beta$がトレーニングデータ${\bf t}$をどれだけ生成しやすいかを表します。エビデンス関数の値が小さければ、その$\alpha,\beta$はそのデータを生成しにくく、逆にエビデンス関数の値が大きければ、そのデータを生成しやすいということになります。つまり、エビデンス関数の値は大きい方が良いということです。エビデンス関数の値が最大になるような超パラメータの値を${\hat\alpha},{\hat\beta}$として、これらを事後予測分布の式に代入することで近似的に
p(t|x,{\bf\Phi},{\bf t}) \approx p(t|x,{\bf\Phi},{\bf t},{\hat\alpha},{\hat\beta})
とするのがエビデンス近似となります。
エビデンス最大化
エビデンス関数が最大になるような$\alpha,\beta$を求めます。${\bf\Phi}^{\rm T}{\bf\Phi}$の固有値を$\lambda_i$として$\alpha,\beta,\gamma$を次のように更新する。
- $\gamma=\sum_i{\beta\lambda_i\over\alpha+\beta\lambda_i}$
- $\alpha={\gamma\over{\bf m}_N^{\rm T}{\bf m}_N}$、$\beta={N-\gamma\over\sum_n\left\{t_n - {\rm m}_N^{\rm T}{\bf\phi}(x_n)\right\}^2}$
この2つのステップを繰り返すことでエビデンス関数が極大になる$\alpha={\hat\alpha},\beta={\hat\beta}$に収束します。この式の導出はPRMLをご覧下さい。
実装
ベイズ曲線フィッティングのときに組んだコードを再利用しています。
計画行列
PolynomialFeaturesクラスは、次数を設定することで入力ベクトル$(x_1,\cdots,x_N)^{\rm T}$を計画行列${\bf\Phi}$に変換します。
import matplotlib.pyplot as plt
import numpy as np
class PolynomialFeatures(object):
def __init__(self, degree):
assert type(degree) is int, "%s is not int" % type(degree)
self.degree = degree
def transform(self, x):
features = [x ** i for i in xrange(self.degree + 1)]
return np.array(features).transpose()
| PolynomialFeatures | メソッドの説明 |
|---|---|
| __init__ | 多項式特徴の次数を設定 |
| transform | 入力を計画行列への変換 |
ベイズ線形回帰
BayesianRegressionクラスでは、ベイズ線形回帰のところで説明した事後確率の推定と事後予測分布の計算を行います。
class BayesianRegression(object):
def __init__(self, alpha=1., beta=1.):
self.alpha = alpha
self.beta = beta
def fit(self, X, t):
self.w_var = np.linalg.inv(
self.alpha * np.identity(np.size(X, 1))
+ self.beta * X.T.dot(X))
self.w_mean = self.beta * self.w_var.dot(X.T.dot(t))
def predict(self, X):
return X.dot(self.w_mean)
def predict_dist(self, X):
y = X.dot(self.w_mean)
y_var = 1 / self.beta + np.sum(X.dot(self.w_var) * X, axis=1)
y_std = np.sqrt(y_var)
return y, y_std
| BayesianRegression | メソッドの説明 |
|---|---|
| __init__ | $\alpha,\beta$の値を設定 |
| fit | パラメータ${\bf w}$の事後分布の平均、分散を計算 |
| predict | 事後予測分布の最頻値を計算 |
| predict_dist | 事後予測分布の最頻値、標準偏差の計算 |
エビデンス近似
パラメータ${\bf w}$の更新と超パラメータ$\alpha,\beta$の更新を交互に行うことでエビデンス関数の最大化を行います。パラメータ${\bf w}$の更新では上のベイズ曲線フィッティングのときと同じことをするだけなので、クラスの継承を用いてメソッドを再利用しています。またevidenceメソッドでは対数エビデンス関数の値を計算します。この値を比べることで複数のモデルのうち良いモデルの選択を自動的に行うことができます。
class EvidenceApproximation(BayesianRegression):
def __init__(self, iter_max=100, alpha=1., beta=1.):
self.iter_max = iter_max
self.alpha = alpha
self.beta = beta
def fit(self, X, t):
M = X.T.dot(X)
eigenvalues = np.linalg.eigvalsh(M)
for i in xrange(self.iter_max):
params = [self.alpha, self.beta]
super(EvidenceApproximation, self).fit(X, t)
self.gamma = np.sum(self.beta * eigenvalues / (self.alpha + self.beta * eigenvalues))
self.alpha = self.gamma / self.w_mean.dot(self.w_mean)
self.beta = (len(t) - self.gamma) / np.sum((t - X.dot(self.w_mean)) ** 2)
if np.allclose(params, [self.alpha, self.beta]):
break
super(EvidenceApproximation, self).fit(X, t)
def evidence(self, X, t):
M = X.T.dot(X)
return (len(M) * np.log(self.alpha)
+ len(t) * np.log(self.beta)
- self.beta * np.sum((t - X.dot(self.w_mean)) ** 2)
- np.linalg.slogdet(self.alpha + self.beta * M)[1])
| EvidenceApproximation | メソッドの説明 |
|---|---|
| __init__ | $\alpha,\beta$の値とそれらを更新する最大の回数を設定 |
| fit | $\alpha,\beta$を推定し、パラメータ${\bf w}$の事後分布の平均、分散を計算 |
| evidence | 対数エビデンス関数の値を計算 |
全体のコード
3次多項式$x(x-5)(x+5)$に従うようなデータ点を生成し、それを0次~7次多項式のモデルでエビデンス近似を用いた曲線フィッティングをして、モデルエビデンスの値が一番大きいモデルを使って事後予測分布を計算しています。
import matplotlib.pyplot as plt
import numpy as np
class PolynomialFeatures(object):
def __init__(self, degree):
assert type(degree) is int, "%s is not int" % type(degree)
self.degree = degree
def transform(self, x):
features = [x ** i for i in xrange(self.degree + 1)]
return np.array(features).transpose()
class BayesianRegression(object):
def __init__(self, alpha=1., beta=1.):
self.alpha = alpha
self.beta = beta
def fit(self, X, t):
self.w_var = np.linalg.inv(
self.alpha * np.identity(np.size(X, 1))
+ self.beta * X.T.dot(X))
self.w_mean = self.beta * self.w_var.dot(X.T.dot(t))
def predict(self, X):
return X.dot(self.w_mean)
def predict_dist(self, X):
y = X.dot(self.w_mean)
y_var = 1 / self.beta + np.sum(X.dot(self.w_var) * X, axis=1)
y_std = np.sqrt(y_var)
return y, y_std
class EvidenceApproximation(BayesianRegression):
def __init__(self, iter_max=100, alpha=1., beta=1.):
self.iter_max = iter_max
self.alpha = alpha
self.beta = beta
def fit(self, X, t):
M = X.T.dot(X)
eigenvalues = np.linalg.eigvalsh(M)
for i in xrange(self.iter_max):
params = [self.alpha, self.beta]
super(EvidenceApproximation, self).fit(X, t)
self.gamma = np.sum(self.beta * eigenvalues / (self.alpha + self.beta * eigenvalues))
self.alpha = self.gamma / self.w_mean.dot(self.w_mean)
self.beta = (len(t) - self.gamma) / np.sum((t - X.dot(self.w_mean)) ** 2)
if np.allclose(params, [self.alpha, self.beta]):
break
super(EvidenceApproximation, self).fit(X, t)
def evidence(self, X, t):
M = X.T.dot(X)
return (len(M) * np.log(self.alpha)
+ len(t) * np.log(self.beta)
- self.beta * np.sum((t - X.dot(self.w_mean)) ** 2)
- np.linalg.slogdet(self.alpha + self.beta * M)[1])
def create_toy_data(func, low=0, high=1, size=10, sigma=1.):
x = np.random.uniform(low, high, size)
t = func(x) + np.random.normal(scale=sigma, size=size)
return x, t
def main():
def func(x):
return x * (x - 5) * (x + 5)
x, t = create_toy_data(func, low=-5, high=5, size=20, sigma=5.)
plt.scatter(x, t, s=50, alpha=0.5, label="observation")
evidences = []
regressions = []
for i in xrange(8):
features = PolynomialFeatures(degree=i)
X = features.transform(x)
regression = EvidenceApproximation(alpha=100., beta=100.)
regression.fit(X, t)
evidences.append(regression.evidence(X, t))
regressions.append(regression)
degree = np.argmax(evidences)
regression = regressions[degree]
x_test = np.linspace(-5, 5, 100)
X_test = PolynomialFeatures(degree=int(degree)).transform(x_test)
y, y_std = regression.predict_dist(X_test)
plt.plot(x_test, func(x_test), color="blue", label="x(x-5)(x+5)")
plt.plot(x_test, y, color="red", label="predict_mean")
plt.fill_between(x_test, y - y_std, y + y_std, color="pink", alpha=0.5, label="predict_std")
plt.legend()
plt.show()
plt.plot(evidences)
plt.title("Model evidence")
plt.xlabel("M")
plt.ylabel("evidence")
plt.show()
if __name__ == '__main__':
main()
- 3次多項式$x(x-5)(x+5)$を定義(
def func()) - その関数に従うノイズ付きのデータ点を作成(
x, t = create_toy_data(...)) - $i = 0,\cdots,7$で4.~6.を繰り返す
- $i$次多項式特徴の計画行列を作成(
X = features.transform(x)) - $\alpha,\beta$の初期値をどちらも100(エビデンス関数の最大化をしなければダメなフィッティングになる値)として、エビデンス近似による曲線フィッティングを行う(
regression.fit(X, t)) - 5.のときの対数エビデンス関数の値を計算して保存(
evidences.append(regression.evidence(X, t))) - 対数エビデンス関数の値が一番大きいモデルの次数を取得(
degree = np.argmax(evidences)) - その次数での回帰の結果を取得(
regression = regressions[degree]) - 以上の結果を図示
結果
PRMLの図3.14のように3次多項式をモデルとしたときの対数エビデンス関数の値が一番大きくなっています。
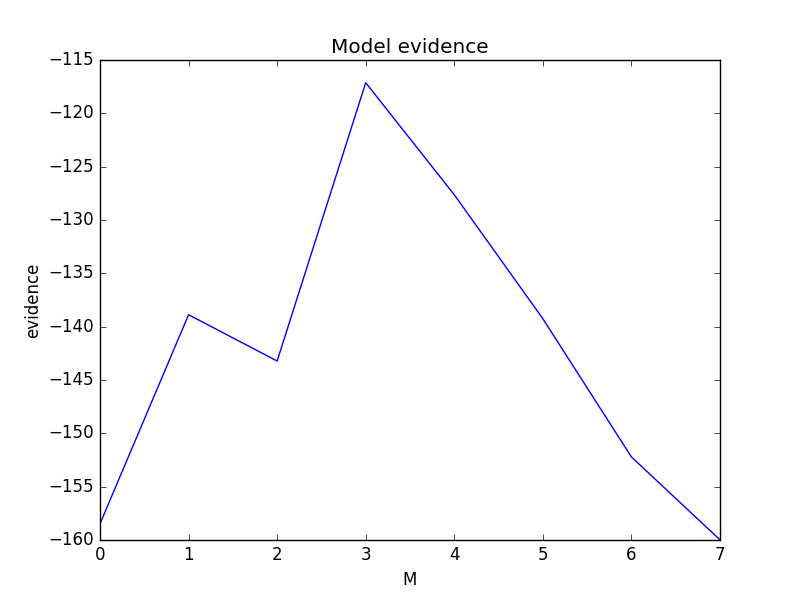
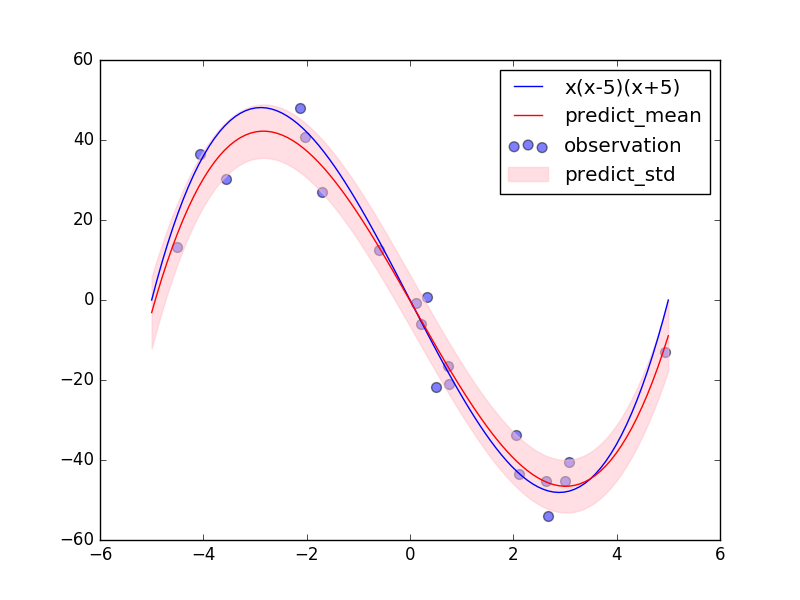
また、その3次多項式のモデルによる予測分布もいい感じになっています。超パラメータ$\alpha,\beta$の初期値をどちらも100にしていたので、普通のベイズ曲線フィッティングであれば、$\alpha$が大きすぎることによって${\bf w}$の各成分の値は0に近く、$\beta$が大きすぎることによって予測分布の分散も小さい、データに対して全くフィッティングできていない事後予測分布が出てきていたはずです。エビデンス関数を最大にする$\alpha,\beta$を推定したので、事後予測分布もデータに合うような結果となっています。
終わりに
このエビデンス近似を用いることでダメダメな超パラメータを初期値にしても良い感じの推定をしてくれました。グリッドサーチとかだとトレーニングデータのうちいくつかの点を検証ようとして超パラメータを探していましたが、エビデンス近似だとトレーニングデータ全てを使って、それも少ない試行回数で超パラメータを推定することができます。また、このエビデンス近似は線形回帰モデルだけでなくロジスティック回帰やニューラルネットワークの超パラメータを推定するのにも用いられるそうです。機会があれば、それらの実装もしていこうと思います。