今回はスチューデントのt分布の最尤推定を実装します。スチューデントのt分布はガウス分布より外れ値に対して頑健な性質を持つ分布としてよく知られていますが、よくよく思い出せばこの分布を用いたことが全くなかったので、良い機会ですしその頑健性を実際に確認してみます。一回目のPRML実装のときに標準ライブラリ以外は極力numpyだけというルールを設けましたが、今回はディガンマ関数というあまり馴染みのない関数が出てきたためscipyも使いました。この企画2回目にして早々にnumpy以外のサードパーティーのパッケージを使ってしまうこととなり、先が思いやられてしまいます。
スチューデントのt分布
スチューデントのt分布は、ガウス分布$\mathcal{N}(x|\mu,\tau^{-1})$の精度パラメータ$\tau$の共役事前分布としてガンマ分布${\rm Gam}(\tau|a,b)$を用い、精度を積分消去して得られる分布です。このことからスチューデントのt分布は、平均は同じだが分散の異なるガウス分布を無限個足し合わせた混合ガウス分布だと解釈できます。
$$p(x|\mu,a,b)=\int^{\infty}_0 \mathcal{N}(x|\mu,\tau^{-1}){\rm Gam}(\tau|a,b){\rm d}\tau$$この後、$\nu=2a,\lambda=a/b$とすると見るスチューデントのt分布の形になります。
$${\rm St}(x|\mu,\lambda,\nu)={\Gamma(\nu/2+1/2)\over\Gamma(\nu/2)}\left({\lambda\over\pi\nu}\right)^{1/2}\left[1+{\lambda(x-\mu)^2\over\nu}\right]^{-\nu/2-1/2}$$幾つかの点xが与えられているときに最尤推定をして$\mu,a,b$(もしくは$\mu,\lambda,\nu$)を推定したいのですが、ガウス分布での最尤推定の場合とは違って閉形式になりません。上の${\rm St}(x|\mu,\lambda,\nu)$をパラメータについて微分しても全然綺麗な形にはなってくれなさそうです。PRMLではスチューデントのt分布の最尤推定にはEMアルゴリズム(PRML演習問題12.24)を使うと書いてあります。EMアルゴリズムとは観測されていないデータがある状況でパラメータを推定するのによく用いられる手法であり、PRMLの第9章で紹介されています。精度パラメータ$\tau$を潜在変数としてEMアルゴリズムを適用します。スチューデントのt分布に適用したときの計算式がPRMLには載っていないので、少し計算していきます。間違いなどがあればご指摘いただけると幸いです。
Eステップ
EMアルゴリズムのE(Expectation)ステップです。このステップでは推定したいパラメータ($\mu,a,b$)を固定して、各サンプル点$x_i$がどんな分散(もしくは精度$\tau$)のガウス分布からサンプルされているのかを計算します。
$$
p(\tau_i|x_i,\mu,a,b) = \mathcal{N}(x_i|\mu,\tau^{-1}){\rm Gam}(\tau_i|a,b)/const.
$$事前分布にはガンマ分布、尤度関数にはガウス関数を用いた形になっています。これを計算するとガンマ分布$${\rm Gam}(\tau_i|a+{1\over2},b+{1\over2}(x_i-\mu)^2)$$が事後分布として得られます。この事後分布の期待値より$$\tau_i={a+{1\over2}\over b+{1\over2}(x_i-\mu)^2}$$として各サンプル点についての精度パラメータが得られます。
Mステップ
EMアルゴリズムのM(Maximization)ステップです。完全データ$\{x_i,\tau_i\}$に対しての対数尤度関数を計算して、パラメータ$\mu,a,b$について最大化します。このときの精度パラメータ$\tau_i$にはEステップで求まったものを用います。
$$\sum_{i=1}^N\ln p(x_i,\tau_i|\mu,a,b) = \sum_{i=1}^N\ln\{\mathcal{N}(x_i|\mu,\tau_i^{-1}){\rm Gam}(\tau_i|a,b)\}$$これを計算して(自信ない)、推定したいパラメータが関わっているところを抜き出してくると、
$$-{1\over2}\sum_i\tau_i(x_i-\mu)^2 + aN\ln b -N\ln\Gamma(a)+a\sum_i\ln\tau_i - b\sum_i\tau_i$$
これをそれぞれのパラメータで微分してイコール0とおいて方程式を解きます。
$$\mu = {\sum_i\tau_ix_i\over\sum_i\tau_i}$$$$a = \psi^{-1}(\ln b + {1\over N}\sum_i\ln\tau_i)$$$$b = {aN\over\sum_i\tau_i}$$aで微分するとディガンマ関数$\psi(x)$がでてきました。もしその関数の逆関数がちゃんと実在するのであれば解けましたが、numpyとかscipyにはディガンマ関数の逆関数なんてない(ディガンマ関数はscipyにある)。ということでパラメータaについては勾配法で少し更新するだけにします。
そもそも$a,b$の解を見るとお互いに混じっているので、上の3つの式では対数尤度関数の最大化はおそらくできていません。このように、対数尤度関数の最大化が完全にはなされない場合のEMアルゴリズムを一般化EMアルゴリズムと呼ぶそうです。スチューデントのt分布の最尤推定を行うときにたいてい自由度パラメータ$\nu(=2a)$を何らかの値で固定しているのは、Mステップをきっちり行うためだと思われます。自由度パラメータを固定すれば、残る推定対象は$\mu,\lambda$となって、対数尤度関数の最大化が簡単にできるのだと思います。
下のコメントをもとに少し訂正、補足をします。本来のEステップであれば、精度パラメータ $\tau_i$の事後分布$p(\tau_i|x_i,\mu,a,b) = {\rm Gam}(\tau_i|a+{1\over2},b+{1\over2}(x_i-\mu)^2)$を計算した部分で終わり、そのあとのMステップでは完全対数尤度関数$\ln p(x_i,\tau_i|\mu,a,b)$のその事後分布についての期待値$\mathbb{E}[\sum_i\ln p(x_i,\tau_i|\mu,a,b)]$を計算します。その計算結果はパラメータに関わっているところだけ抜き出すと、$-{1\over2}\sum_i\mathbb{E}[\tau_i](x_i - \mu)^2 + a\sum_i\mathbb{E}[\ln\tau_i] + aN\ln b - b\sum_i\mathbb{E}[\tau_i] - N\ln\Gamma(a)$、となり最大化すべき関数の形が一部違っています。元の記事の方のEMアルゴリズムは期待値計算にサンプル近似$\mathbb{E}[\sum_i\ln p(x_i,\tau_i|\mu,a,b)]=\sum_i\ln p(x_i,\tau_i^{(sample)}|\mu,a,b)$、ただしサンプルサイズはそれぞれ1つだけで常に$\tau_i^{(sample)}=\mathbb{E}[\tau_i]$がサンプルされる、を用いていると解釈してもらえれば幸いです。下の図ではある程度うまくいっているように見えるので、このサンプル近似でもそれほど精度に影響がないのかもしれません(本当にそうならうれしいな〜)。
最尤推定の流れ
ここまでのことをまとめますと、
- パラメータ$\mu,a,b$の初期値を設定
- Eステップで全てのサンプル点に対して精度パラメータ$\tau$を計算
- Mステップで完全データに対する対数尤度関数の値が大きくなるようにパラメータ$\mu,a,b$を更新
- パラメータが収束していれば終了、そうでなければEステップに戻る
このような一般化EMアルゴリズムを用いてスチューデントのt分布のパラメータを求めます。
実装
import
結果の図示をするためのmatplotlibとnumpy、そしてそれらに加えてscipyからガンマ関数とディガンマ関数をimportします。
import matplotlib.pyplot as plt
import numpy as np
from scipy.special import gamma, digamma
ガウス分布
スチューデントのt分布との比較をするためだけのガウス分布による最尤推定
class Gaussian(object):
def fit(self, x):
self.mean = np.mean(x)
self.var = np.var(x)
def predict_proba(self, x):
return (np.exp(-0.5 * (x - self.mean) ** 2 / self.var)
/ np.sqrt(2 * np.pi * self.var))
スチューデントのt分布
スチューデントのt分布による最尤推定を行うコードです。fitメソッドで最尤推定を行っています。その中でEステップとMステップを繰り返し、パラメータが更新されなくなったら終了します。
class StudentsT(object):
def __init__(self, mean=0, a=1, b=1, learning_rate=0.01):
self.mean = mean
self.a = a
self.b = b
self.learning_rate = learning_rate
def fit(self, x):
while True:
params = [self.mean, self.a, self.b]
self._expectation(x)
self._maximization(x)
if np.allclose(params, [self.mean, self.a, self.b]):
break
def _expectation(self, x):
self.precisions = (self.a + 0.5) / (self.b + 0.5 * (x - self.mean) ** 2)
def _maximization(self, x):
self.mean = np.sum(self.precisions * x) / np.sum(self.precisions)
a = self.a
b = self.b
self.a = a + self.learning_rate * (
len(x) * np.log(b)
+ np.log(np.prod(self.precisions))
- len(x) * digamma(a))
self.b = a * len(x) / np.sum(self.precisions)
def predict_proba(self, x):
return ((1 + (x - self.mean) ** 2/(2 * self.b)) ** (-self.a - 0.5)
* gamma(self.a + 0.5)
/ (gamma(self.a) * np.sqrt(2 * np.pi * self.b)))
コード全体
import matplotlib.pyplot as plt
import numpy as np
from scipy.special import gamma, digamma
class Gaussian(object):
def fit(self, x):
self.mean = np.mean(x)
self.var = np.var(x)
def predict_proba(self, x):
return (np.exp(-0.5 * (x - self.mean) ** 2 / self.var)
/ np.sqrt(2 * np.pi * self.var))
class StudentsT(object):
def __init__(self, mean=0, a=1, b=1, learning_rate=0.01):
self.mean = mean
self.a = a
self.b = b
self.learning_rate = learning_rate
def fit(self, x):
while True:
params = [self.mean, self.a, self.b]
self._expectation(x)
self._maximization(x)
if np.allclose(params, [self.mean, self.a, self.b]):
break
def _expectation(self, x):
self.precisions = (self.a + 0.5) / (self.b + 0.5 * (x - self.mean) ** 2)
def _maximization(self, x):
self.mean = np.sum(self.precisions * x) / np.sum(self.precisions)
a = self.a
b = self.b
self.a = a + self.learning_rate * (
len(x) * np.log(b)
+ np.log(np.prod(self.precisions))
- len(x) * digamma(a))
self.b = a * len(x) / np.sum(self.precisions)
def predict_proba(self, x):
return ((1 + (x - self.mean) ** 2/(2 * self.b)) ** (-self.a - 0.5)
* gamma(self.a + 0.5)
/ (gamma(self.a) * np.sqrt(2 * np.pi * self.b)))
def main():
# create toy data including outliers and plot histogram
x = np.random.normal(size=20)
x = np.concatenate([x, np.random.normal(loc=20., size=3)])
plt.hist(x, bins=50, normed=1., label="samples")
# prepare model
students_t = StudentsT()
gaussian = Gaussian()
# maximum likelihood estimate
students_t.fit(x)
gaussian.fit(x)
# plot results
x = np.linspace(-5, 25, 1000)
plt.plot(x, students_t.predict_proba(x), label="student's t", linewidth=2)
plt.plot(x, gaussian.predict_proba(x), label="gaussian", linewidth=2)
plt.legend()
plt.show()
if __name__ == '__main__':
main()
結果
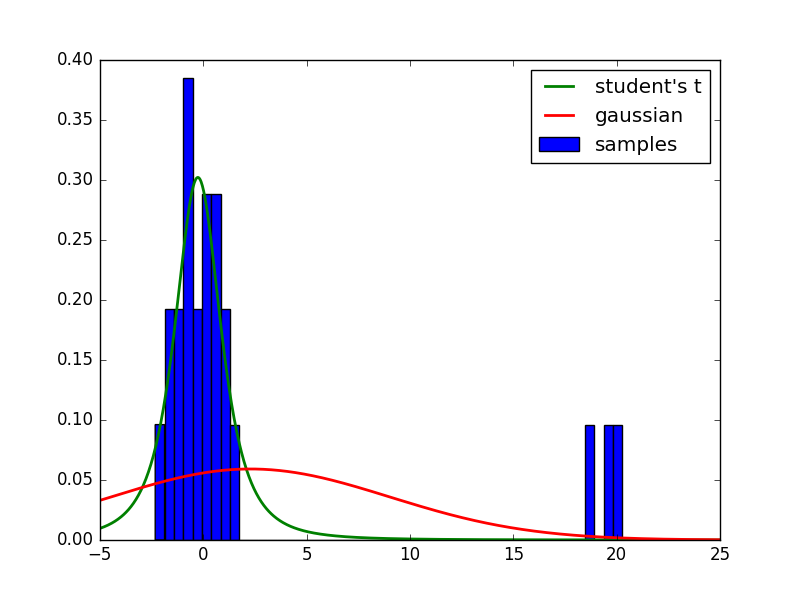
上のコードを走らせると下のような結果が得られると思います。PRMLの図2.16のようにスチューデントのt分布によるフィッティングだと確かに外れ値がある場合でも頑健です。スチューデントのt分布の平均は0あたりですが、ガウス分布の平均は外れ値に引っ張られて2.5あたりになっています。
終わりに
スチューデントのt分布での最尤推定のほうがガウス分布をモデルにした場合より頑健であることが確認できました。機会があればスチューデントのt分布を使った曲線の回帰問題も解いてみようかと思います。