PRML第6章 ガウス過程による回帰 Python実装

ほぼNumpyだけでPRMLのアルゴリズムを実装する企画ですが、はやくも日本語版PRMLでは下巻に突入しました。
第６章のカーネル法では、カーネル関数を用いてデータ点の特徴空間での内積を計算して（カーネルトリック）、その空間で線形回帰や線形分離します。ガウス過程については全然詳しく知らないので間違っていることが多々あると思います。いちおうコードに関してはそれっぽく動く実装ができています。

ガウス過程

第３章などで取り組んだ線形回帰では、パラメータ${\bf w}$はよくガウス分布に従っていました。なので、$y={\bf w}^{\rm T}\phi(x)$も１次元のガウス分布に従い、${\bf y}={\bf\Phi}{\bf w}$は多次元のガウス分布に従います。ただし、${\bf\Phi}$は$\{x_1,\dots,x_N\}$の計画行列。
このような場合、$p({\bf y})$はガウス過程に従うといいます。ガウス過程は、一次元($y$がスカラー)、多次元($y$が有限個のベクトル)、などに限らず無限次元($y$が無限個のベクトル)でもガウス分布に従う、いわば無限次元のガウス分布と解釈できるそうです。

${\bf y}$の同時分布は平均が${\bf 0}$、共分散にグラム行列$K$としたガウス分布

p({\bf y}) = \mathcal{N}({\bf y}|{\bf 0},K)

となる。ただし、グラム行列の要素は$k(x,x')$をカーネル関数として、$K_{nm}=k(x_n,x_m)$となります。カーネル関数としては、$a,b$を定数としてガウス関数$k(x,x')=a\exp\left(-b(x - x')^2\right)$などがよく使われています。お互いに似ている$x_n,x_m$に対しては、$y(x_n),y(x_m)$の相関が高くなるように定められます。この「似ている」はカーネル関数としてどのようなものを用いるのかに依ります。

ガウス過程による回帰

観測されるターゲットを$t_n=y_n + \epsilon_n$とします。ここで$y_n={\bf w}^{\rm T}\phi(x_n)$、ノイズ$\epsilon_n$はn番目の観測値に加わるガウス分布に従うノイズとします。精度パラメータ$\beta$を用いると

p(t_n|y_n) = \mathcal{N}(t_n|y_n,\beta^{(-1)})

となります。よって、${\bf t}=(t_1,\dots,t_N)^{\rm T}$として、

p({\bf t}|{\bf y}) = \mathcal{N}({\bf t}|{\bf y},\beta^{(-1)}{\bf I}_N)

となります。ここで${\bf y}$の同時確率はすでに上で定義したので、${\bf t}$の同時分布が求まります。

\begin{align}
p({\bf t}) &= \int p({\bf t}|{\bf y})p({\bf y})d{\bf y}\\
&= \int \mathcal{N}({\bf t}|{\bf y},\beta^{(-1)}{\bf I}_N)\mathcal{N}({\bf y}|{\bf 0},K)d{\bf y}\\
&= \mathcal{N}({\bf t}|{\bf 0},{\bf C}_N)
\end{align}

ただし、${\bf C}_N = K + \beta^{(-1)}{\bf I}_N$としています。

N個の観測値${\bf t}$に加えて新たに予測したい$t_{N+1}$として、${\bf t},t_{N+1}$の同時確率は、上の議論より

p({\bf t},t_{N+1}) = \mathcal{N}({\bf t},t_{N+1}|{\bf 0}, {\bf C}_{N+1})

ただし、共分散行列は、${\bf k} = \left(k(x_1,x_{N+1}),\dots,k(x_N,x_{N+1})\right),c=k(x_{N+1},x_{N+1})$として

{\bf C}_{N+1} =
\begin{bmatrix}
{\bf C}_N & {\bf k}\\
{\bf k}^{\rm T} & c
\end{bmatrix}

となります。${\bf t},t_{N+1}$の同時分布が分かったので、条件付き分布$p(t_{N+1}|{\bf t})$が求まります。

p(t_{N+1}|{\bf t}) = \mathcal{N}(t_{N+1}|{\bf k}^{\rm T}{\bf C}_N^{-1}{\bf t},c-{\bf k}^{\rm T}{\bf C}_N^{-1}{\bf k})

超パラメータの学習

上での議論はカーネル関数$k(x,x')$を固定していました。例えば、カーネル関数$k(x,x') = a\exp(-b(x - x')^2)$において$a,b$を定数としていました。すると、カーネル関数に用いる定数をどうすればいいのかということになります。このパラメータの推定はPRMLの第３章で実装した超パラメータの推定に対応しています。そのときはエビデンス関数$p({\bf t}|\theta)$の最大化をしました。$\theta$はカーネル関数のパラメータ、例えば$\theta=(a,b)^{\rm T}$。
対数エビデンス関数は

\ln p({\bf t}|\theta) = -{1\over2}\ln |{\bf C}_N| - {1\over2}{\bf t}^{\rm T}{\bf C}_N^{-1}{\bf t} - {N\over2}\ln(2\pi)

となり、これをパラメータについて微分すると、

{\partial\over\partial\theta_i}\ln p({\bf t}|\theta) = -{1\over2}{\rm Tr}({\bf C}_N^{-1}{\partial{\bf C}_N\over\partial\theta_i}) + {1\over2}{\bf t}^{\rm T}{\bf C}_N^{-1}{\partial{\bf C}_N\over\partial\theta_i}{\bf C}_N^{-1}{\bf t}

となります。勾配法を使ってパラメータの更新をしていきました。

実装

ライブラリ

import matplotlib.pyplot as plt
import numpy as np

importするライブラリはグラフ描画用ライブラリであるmatplotlibと行列計算などを行うnumpyの２つです。

カーネル関数

今回はカーネル関数として$a\exp(-{b\over2}(x-x')^2)$を使いました。

# カーネル関数のクラス
class GaussianKernel(object):
    # カーネル関数のパラメータa,bを初期化
    def __init__(self, params):
        assert np.shape(params) == (2,)
        self.__params = params

    # カーネル関数のパラメータa,bを返す
    def get_params(self):
        return np.copy(self.__params)

     # x,yを入力としてカーネル関数の値を計算 PRML式(6.63)
    def __call__(self, x, y):
        return self.__params[0] * np.exp(-0.5 * self.__params[1] * (x - y) ** 2)

    # x,yを入力とした時のカーネル関数のパラメータでの微分を計算
    def derivatives(self, x, y):
        sq_diff = (x - y) ** 2
        # パラメータaでの微分
        delta_0 = np.exp(-0.5 * self.__params[1] * sq_diff)
        # パラメータbでの微分
        delta_1 = -0.5 * sq_diff * delta_0 * self.__params[0]
        return (delta_0, delta_1)

    # カーネル関数のパラメータを更新
    def update_parameters(self, updates):
        assert np.shape(updates) == (2,)
        self.__params += updates

ガウス過程による回帰

# ガウス過程による回帰を行うクラス
class GaussianProcessRegression(object):
    # カーネル関数とノイズの精度パラメータの初期化
    def __init__(self, kernel, beta=1.):
        self.kernel = kernel
        self.beta = beta

    # カーネル関数のパラメータ推定を行わずに回帰
    def fit(self, x, t):
        self.x = x
        self.t = t
        # グラム行列の計算 PRML式(6.54)
        Gram = self.kernel(*np.meshgrid(x, x))
        # 共分散行列の計算 PRML式(6.62)
        self.covariance = Gram + np.identity(len(x)) / self.beta
        # 精度行列の計算
        self.precision = np.linalg.inv(self.covariance)

    # カーネル関数のパラメータの推定を行う回帰
    def fit_kernel(self, x, t, learning_rate=0.1, iter_max=10000):
        for i in xrange(iter_max):
            params = self.kernel.get_params()
            # カーネル関数の今のパラメータで回帰
            self.fit(x, t)
            # 対数エビデンス関数をパラメータで微分
            gradients = self.kernel.derivatives(*np.meshgrid(x, x))
            # パラメータの更新量を計算 PRML式(6.70)
            updates = np.array(
                [-np.trace(self.precision.dot(grad)) + t.dot(self.precision.dot(grad).dot(self.precision).dot(t)) for grad in gradients])
            # パラメータを更新
            self.kernel.update_parameters(learning_rate * updates)
            # パラメータの更新量が小さければ更新をやめる
            if np.allclose(params, self.kernel.get_params()):
                break
        else:
            # 既定の更新回数だけ更新してもパラメータの更新量が小さくない場合以下の文を出力
            print "parameters may not have converged"

    # 予測分布を出力
    def predict_dist(self, x):
        K = self.kernel(*np.meshgrid(x, self.x, indexing='ij'))
        # 予測分布の平均を計算 PRML式(6.66)
        mean = K.dot(self.precision).dot(self.t)
        # 予測分布の分散を計算 PRML式(6.67)
        var = self.kernel(x, x) + 1 / self.beta - np.sum(K.dot(self.precision) * K, axis=1)
        return mean.ravel(), np.sqrt(var.ravel())

メイン関数

regression.fit_kernel(...)をregression.fit(x,t)に置き換えるとパラメータの推定を行わずに回帰します。

def main():
    # 学習データが従う関数を設定
    def func(x):
        return np.sin(2 * np.pi * x)
    # 学習データを生成
    x, t = create_toy_data(func, high=0.7, std=0.1)

    # カーネル関数の設定、パラメータはてきとうに設定
    kernel = GaussianKernel(params=np.array([1., 1.]))
    # ガウス過程回帰に用いるカーネル関数と精度パラメータ(真の値)の設定
    regression = GaussianProcessRegression(kernel=kernel, beta=100)
    # カーネル関数のパラメータの推定も含めた回帰、regression.fit(x,t)に替えるとパラメータを推定せず回帰
    regression.fit_kernel(x, t, learning_rate=0.1, iter_max=10000)

    # テストデータについて予測分布を出力
    x_test = np.linspace(0, 1, 100)
    y, y_std = regression.predict_dist(x_test)

    # 回帰の結果をプロット
    plt.scatter(x, t, alpha=0.5, color="blue", label="observation")
    plt.plot(x_test, func(x_test), color="blue", label="sin$(2\pi x)$")
    plt.plot(x_test, y, color="red", label="predict_mean")
    plt.fill_between(x_test, y - y_std, y + y_std, color="pink", alpha=0.5, label="predict_std")
    plt.legend(loc="lower left")
    plt.show()

コード全体

gaussian_process_regression.py

import matplotlib.pyplot as plt
import numpy as np


class GaussianKernel(object):

    def __init__(self, params):
        assert np.shape(params) == (2,)
        self.__params = params

    def get_params(self):
        return np.copy(self.__params)

    def __call__(self, x, y):
        return self.__params[0] * np.exp(-0.5 * self.__params[1] * (x - y) ** 2)

    def derivatives(self, x, y):
        sq_diff = (x - y) ** 2
        delta_0 = np.exp(-0.5 * self.__params[1] * sq_diff)
        delta_1 = -0.5 * sq_diff * delta_0 * self.__params[0]
        return (delta_0, delta_1)

    def update_parameters(self, updates):
        assert np.shape(updates) == (2,)
        self.__params += updates


class GaussianProcessRegression(object):

    def __init__(self, kernel, beta=1.):
        self.kernel = kernel
        self.beta = beta

    def fit(self, x, t):
        self.x = x
        self.t = t
        Gram = self.kernel(*np.meshgrid(x, x))
        self.covariance = Gram + np.identity(len(x)) / self.beta
        self.precision = np.linalg.inv(self.covariance)

    def fit_kernel(self, x, t, learning_rate=0.1, iter_max=10000):
        for i in xrange(iter_max):
            params = self.kernel.get_params()
            self.fit(x, t)
            gradients = self.kernel.derivatives(*np.meshgrid(x, x))
            updates = np.array(
                [-np.trace(self.precision.dot(grad)) + t.dot(self.precision.dot(grad).dot(self.precision).dot(t)) for grad in gradients])
            self.kernel.update_parameters(learning_rate * updates)
            if np.allclose(params, self.kernel.get_params()):
                break
        else:
            print "parameters may not have converged"

    def predict_dist(self, x):
        K = self.kernel(*np.meshgrid(x, self.x, indexing='ij'))
        mean = K.dot(self.precision).dot(self.t)
        var = self.kernel(x, x) + 1 / self.beta - np.sum(K.dot(self.precision) * K, axis=1)
        return mean.ravel(), np.sqrt(var.ravel())


def create_toy_data(func, low=0, high=1., n=10, std=1.):
    x = np.random.uniform(low, high, n)
    t = func(x) + np.random.normal(scale=std, size=n)
    return x, t


def main():

    def func(x):
        return np.sin(2 * np.pi * x)

    x, t = create_toy_data(func, high=0.7, std=0.1)

    kernel = GaussianKernel(params=np.array([1., 1.]))
    regression = GaussianProcessRegression(kernel=kernel, beta=100)
    regression.fit_kernel(x, t, learning_rate=0.1, iter_max=10000)

    x_test = np.linspace(0, 1, 100)
    y, y_std = regression.predict_dist(x_test)

    plt.scatter(x, t, alpha=0.5, color="blue", label="observation")
    plt.plot(x_test, func(x_test), color="blue", label="sin$(2\pi x)$")
    plt.plot(x_test, y, color="red", label="predict_mean")
    plt.fill_between(x_test, y - y_std, y + y_std, color="pink", alpha=0.5, label="predict_std")
    plt.legend(loc="lower left")
    plt.show()

if __name__ == '__main__':
    main()

結果

PRMLの図6.8のような図ができました。学習データのない領域では予測分布の分散が大きく、学習データのあるところでは分散が小さくなっています。

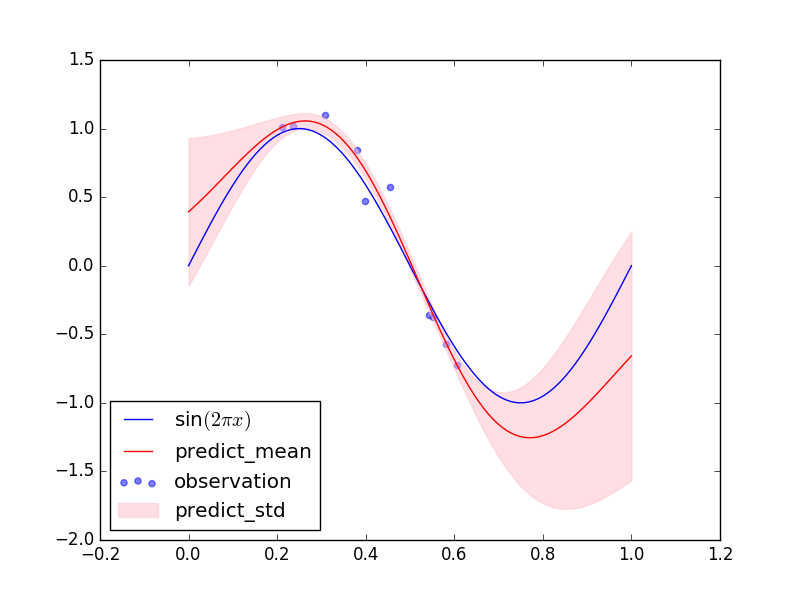
ちなみに上と同じ学習データで超パラメータの最尤推定を行わなかった場合の結果は下の図のようになりました。学習データについても（テストデータについても）上の予測分布の方がフィッティングできています。

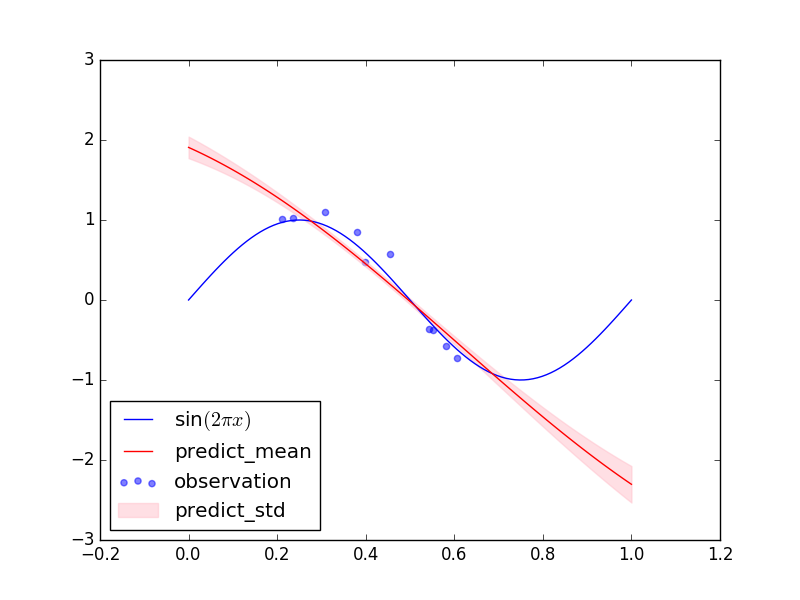
終わりに

結局やっていることはベイズ線形回帰と同じようなものです。ただ、特徴ベクトルを明示的に用いずに、カーネルトリックを用いて特徴ベクトルの内積だけ使って回帰しました。PRMLには記載されていませんが、ガウス過程はベイズ最適化という最近注目を集めているらしい手法に用いられるているそうです。ベイズ最適化を使って、ニューラルネットワークの学習係数などのパラメータを決定するらしいです。機会があればベイズ最適化を実装してみたいです。