PRML第5章 混合密度ネットワーク Python実装

前回は普通のニューラルネットワークをtensorflowやchainerなどのライブラリを使わずに実装しました。ただ、その類の実装はネット上にすでにたくさんあり、それではあまり面白みがありませんので、前回のはあくまで準備として今回は混合密度ネットワークを実装しました。前回実装したニューラルネットワークのコードを利用するので、前回の記事も適宜参考にしてみて下さい。

混合密度ネットワーク

従来モデルの問題点

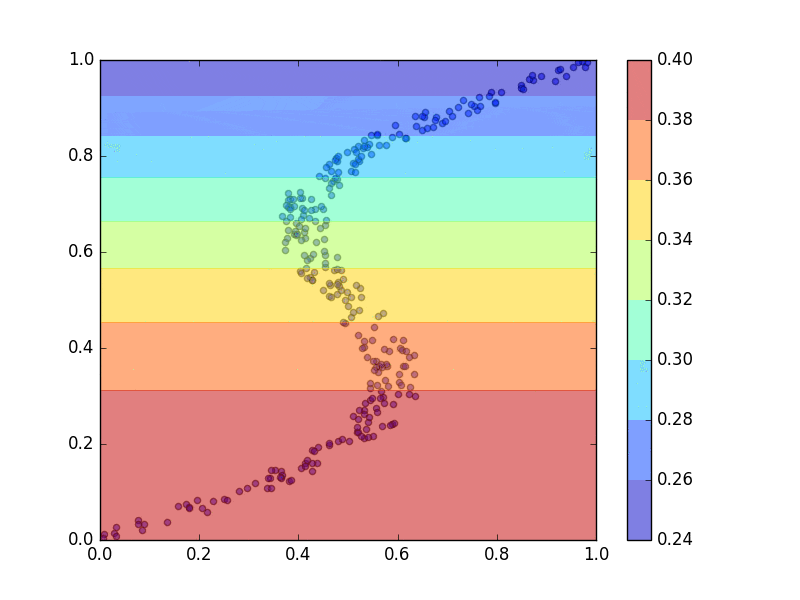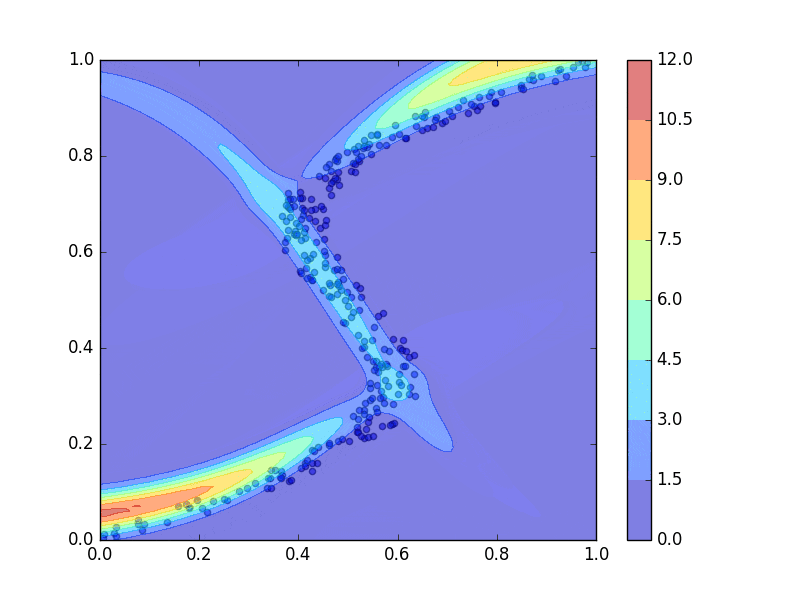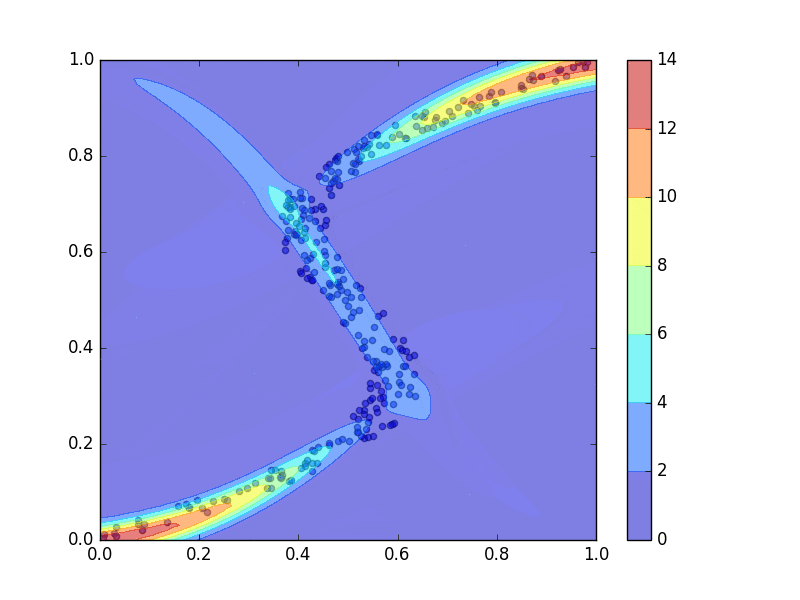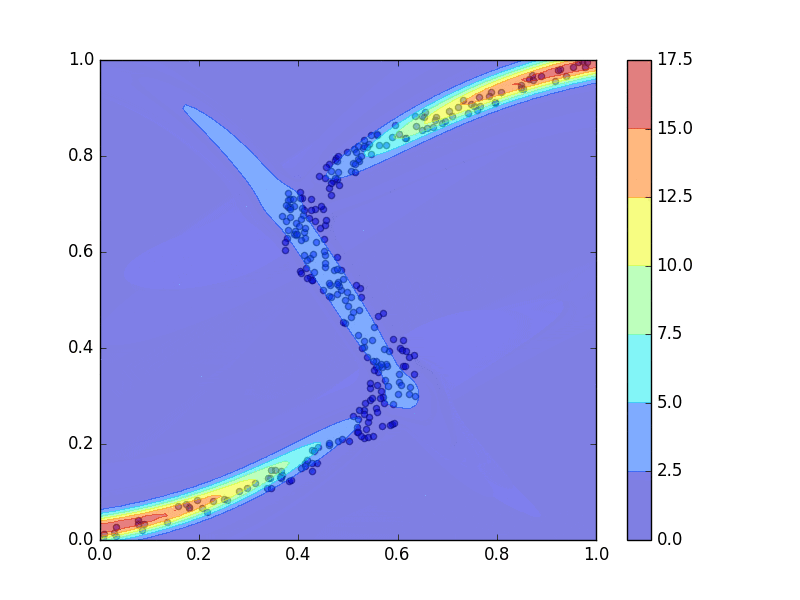
回帰問題を解くときに、二乗和誤差関数を使っていたのではうまく対処できない場合があります。下の図（PRML図5.19の再現）は、青点をトレーニングデータとして、二乗和誤差関数を用いてニューラルネットワークを学習させたときの結果を表しています。

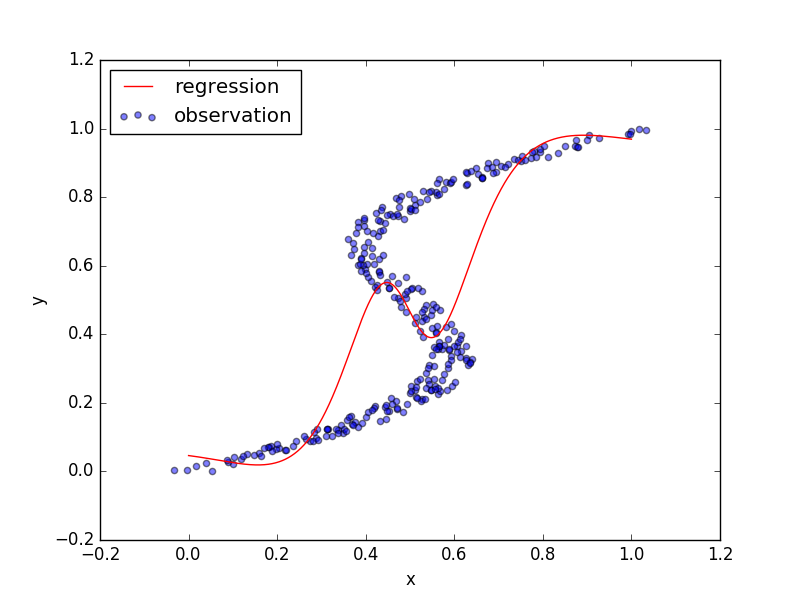
$x=0.5$のときは$y$の値が0.2、0.5、0.8のどれでもよさそうです。しかし、その中で一つを選ばないといけないので0.5になり、他の２つにフィッティングしません。ニューラルネットワークを学習させたのにあまりフィッティングできていないのは、コスト関数が単峰性のガウス分布でモデルされているからです。入力$x$とターゲット$t$の関係を、ガウス分布で以下のように表し、

p(t|x) = \mathcal{N}(t|\mu(x),\sigma^2),

これに基づいてフィッティング、関数$\mu(x)$の推定、を行っていました。そして、推定した$\mu(x)$が上の図の赤色となっていて、ダメダメな結果となってしまいました。

混合ガウス分布

混合密度ネットワークではコスト関数に多峰性の混合ガウス分布でモデルされたものを用いることで、上の問題を解決します。K個のガウス分布に一つ一つ混合係数$\pi_k$を用意して、入力$x$とターゲット$t$の関係を

p(t|x) = \sum_{k=1}^K\pi_k(x)\mathcal{N}(t|\mu_k(x),\sigma^2_k(x))

とモデルします。ただし、混合係数の和は1とします($\sum_k\pi_k=1$)。上のトレーニングデータの例だと、$x=0.5$では$y=0.2,0.5,0.8$のあたりに３つのデータ点の集合があります。よって、$K=3$とするのが良さそうです。3個のガウス分布がそれぞれ別のデータ点の集合にフィッティングされることで、多峰性のあるデータでも対処できます。
よって、トレーニングデータの組$\{x_n,t_n\}_{n=1}^N$が与えられているとき、最適化するコスト関数は

\begin{align}
E(w) &= \sum_{n=1}^N E_n\\
&= -\sum_{n=1}^N \ln p(t_n|x_n)\\
&= -\sum_{n=1}^N \ln \left\{\sum_{k=1}^K\pi_k(x_n,w)\mathcal{N}\left(t_n|\mu_k(x_n,w),\sigma^2_k(x_n,w)\right)\right\}
\end{align}

となります。そして、上の式を最小化するようなパラメータ$w$を推定します。関数$\pi_k,\mu_k,\sigma_k$にはニューラルネットワークを使います。パラメータ$w$のネットワークに入力$x$を入れると、混合係数、平均、分散が出力され、$t$の確率分布が算出されます。

ネットワーク構造

今回は上の図のようなデータに対して回帰を行うので、入力${\bf x}$は１次元となります。中間${\bf z}$のノードの数はPRMLにならって5つ、出力${\bf y}$のノード数は９つとします。第一層のパラメータを$W^{(1)},{\bf b}^{(1)}$、活性化関数を$f(\cdot)$、第二層のパラメータを$W^{(2)},{\bf b}^{(2)}$として、順伝播は次のようになります。

\begin{align}
{\bf z} &= f(W^{(1)}{\bf x} + {\bf b}^{(1)})\\
{\bf y} &= W^{(2)}{\bf z} + {\bf b}^{(2)}
\end{align}

この出力9つは混合ガウス分布のパラメータ$\pi_k,\mu_k,\sigma_k$の活性です。
まず、出力${\bf y}$は上から３つずつ$\pi,\mu,\sigma$に対応している活性とします。

{\bf y} =
\begin{bmatrix}
a_{\pi_1}\\
a_{\pi_2}\\
a_{\pi_3}\\
a_{\mu_1}\\
a_{\mu_2}\\
a_{\mu_3}\\
a_{\sigma_1}\\
a_{\sigma_2}\\
a_{\sigma_3}
\end{bmatrix}

混合係数$\pi_k$は$\sum_k\pi_k=1$という制約条件があるので、ソフトマックス関数により混合係数を出力します。

\pi_k = {\exp(a_{\pi_k})\over\sum_{l=1}^K\exp(a_{\pi_l})}

平均は非線形変換を用いずに$\mu_k = a_{\mu_k}$とします。
標準偏差$\sigma$は０以上なので指数関数を使って$\sigma_k = \exp(a_{\sigma_k})$。
これで、混合ガウス分布を計算するのに必要な関数$\pi_k,\mu_k,\sigma_k$が求まりました。

勾配

前回のニューラルネットワークの実装で書いたようにニューラルネットワークを学習させるのにはコスト関数をニューラルネットワークの出力で微分した勾配が必要です。それがあれば、あとは誤差逆伝播を使ってコスト関数のパラメータ$w$についての微分も計算できます。
そのコスト関数のニューラルネットワークの出力での勾配は、

\gamma_{nk}(t_n|x_n) = {\pi_k\mathcal{N}(t_n|\mu_k(x_n,w),\sigma_k^2(x_n,w))\over\sum_l\pi_l\mathcal{N}(t_n|\mu_l(x_n,w),\sigma_l^2(x_n,w))}

を用いて、

\begin{align}
{\partial E_n\over\partial a_{\pi_k}} &= \pi_k - \gamma_{nk}\\
{\partial E_n\over\partial a_{\mu_k}} &= \gamma_{nk}{\mu_k - t_n\over\sigma^2_k}\\
{\partial E_n\over\partial a_{\sigma_k}} &= \gamma_{nk}\left(1 - {||t_n - \mu_k||^2\over \sigma^2_k}\right)
\end{align}

となります。式の導出はPRMLでは演習問題になっているのでその回答、もしくは混合密度ネットワークの論文を参照してください。

実装

コスト関数

上で書いた数式をコードにすると、次のようになります。

# コスト関数のクラス
class GaussianMixture(object):
    """Negative Log Likelihood of Gaussian Mixture model"""
    def __init__(self, n_components):
        # ガウス分布の個数、今までの例だと3
        self.n_components = n_components

    # コスト関数の値を計算するメソッド
    def __call__(self, X, targets):

        # ネットワークの出力Xを活性化関数で変換して、標準偏差、混合係数、平均を計算
        sigma, weight, mu = self.activate(X)

        # ガウス関数N(t|mu,sigma^2)の値を計算
        gauss = self.gauss(mu, sigma, targets)

        # 混合ガウス分布の負の対数尤度E(w):PRML(式5.153)
        return -np.sum(np.log(np.sum(weight * gauss, axis=1)))

    # 活性化関数で変換
    def activate(self, X):
        assert np.size(X, 1) == 3 * self.n_components

        # Xを標準偏差、混合係数、平均に対応するところに分割
        X_sigma, X_weight, X_mu = np.split(X, [self.n_components, 2 * self.n_components], axis=1)

        # 標準偏差を活性化関数で変換
        sigma = np.exp(X_sigma)

        # 混合係数を活性化関数で変換、桁があふれないように最大値で引く
        weight = np.exp(X_weight - np.max(X_weight, 1, keepdims=True))
        weight /= np.sum(weight, axis=1, keepdims=True)

        return sigma, weight, X_mu

    # ガウス関数N(target|mu,sigma^2)を計算
    def gauss(self, mu, sigma, targets):
        return np.exp(-0.5 * (mu - targets) ** 2 / np.square(sigma)) / np.sqrt(2 * np.pi * np.square(sigma))

    # コスト関数を活性で微分
    def delta(self, X, targets):
        sigma, weight, mu = self.activate(X)
        var = np.square(sigma)
        gamma = weight * self.gauss(mu, sigma, targets)
        gamma /= np.sum(gamma, axis=1, keepdims=True)

        # それぞれの微分を計算
        delta_mu = gamma * (mu - targets) / var
        delta_sigma = gamma * (1 - (mu - targets) ** 2 / var)
        delta_weight = weight - gamma

        # 連結させてから返す
        delta = np.hstack([delta_sigma, delta_weight, delta_mu])
        return delta

学習データの作成

# 関数funcの逆関数に従うような学習データを作成する
def create_toy_dataset(func, n=300):
    t = np.random.uniform(size=(n, 1))
    x = func(t) + np.random.uniform(-0.05, 0.05, size=(n, 1))
    return x, t

ミニバッチ処理

学習がうまくいかないことがあったので急遽使用した手法の一つ。
学習データ全てを使って勾配を計算するのではなく、学習データからいくつかを取ってきて勾配計算を行う。こうすることで、局所解から抜け出せるかもしれません。

# 学習データの組x,tからランダムにペアをn個選択する
def sample(x, t, n=None):
    assert len(x) == len(t)
    N = len(x)
    if n is None:
        n = N
    indices = np.random.choice(N, n, replace=False)
    return x[indices], t[indices]

混合密度ネットワークの学習

混合密度ネットワークを学習して、その結果を図示するメインの関数です。

def main():

    def func(x):
        return x + 0.3 * np.sin(2 * np.pi * x)

    # 関数funcの逆関数に従うデータ点を生成
    x, t = create_toy_dataset(func)

    # ニューラルネットワークの構造を決める。
    layers = [TanhLayer(1, 5, std=0.1), LinearLayer(5, 9, std=0.1)]
    # 最適化するコスト関数を決める
    cost_function = GaussianMixture(3)
    # ニューラルネットワークを作る
    nn = NeuralNetwork(layers, cost_function)
    # 実装がうまくいっているかチェックする場合はこの下の行をアンコメントする。
    # nn._gradient_check(np.array([[0.5]]), np.array([[0.5]]))

    # はじめの学習係数を設定
    learning_rate = 1e-4
    for i in xrange(500000):
        # 一万回に一回コスト関数の値を算出し、学習係数を0.9倍にする
        if i % 10000 == 0:
            print "step %6d, cost %f" % (i, nn.cost(x, t))
            learning_rate *= 0.9
        # ミニバッチ処理
        batch = sample(x, t, n=100)
        nn.fit(*batch, learning_rate=learning_rate)

    # テスト用データの作成
    x_test = np.linspace(x.min(), x.max(), 100)
    y_test = np.linspace(t.min(), t.max(), 100)
    X_test, Y_test = np.meshgrid(x_test, y_test)
    test = np.array([X_test, Y_test]).transpose(1, 2, 0).reshape(-1, 2)

    # テスト用データの尤度を算出
    sigma, weight, mu = nn(test[:, 0].reshape(-1, 1))
    probs = cost_function.gauss(mu, sigma, test[:, 1].reshape(-1, 1))
    probs = np.sum(weight * probs, axis=1)
    Probs = probs.reshape(100, 100)

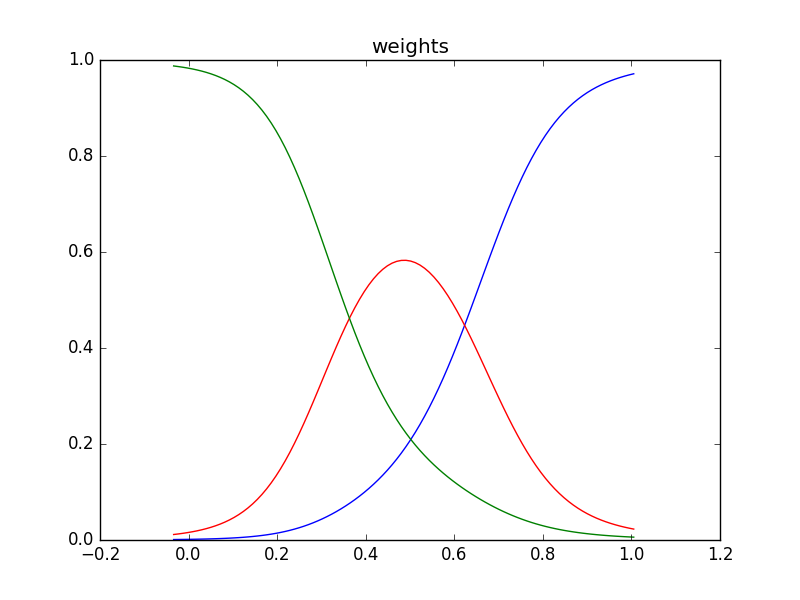
    # PRML図5.21(a)の再現
    plt.plot(x_test, weight[:100, 0], color="blue")
    plt.plot(x_test, weight[:100, 1], color="red")
    plt.plot(x_test, weight[:100, 2], color="green")
    plt.title("weights")
    plt.show()

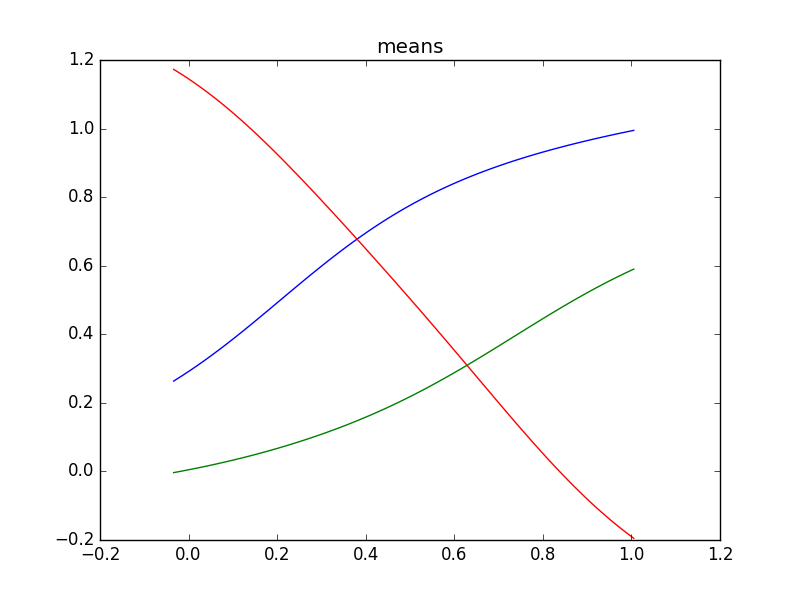
    # PRML図5.21(b)の再現
    plt.plot(x_test, mu[:100, 0], color="blue")
    plt.plot(x_test, mu[:100, 1], color="red")
    plt.plot(x_test, mu[:100, 2], color="green")
    plt.title("means")
    plt.show()

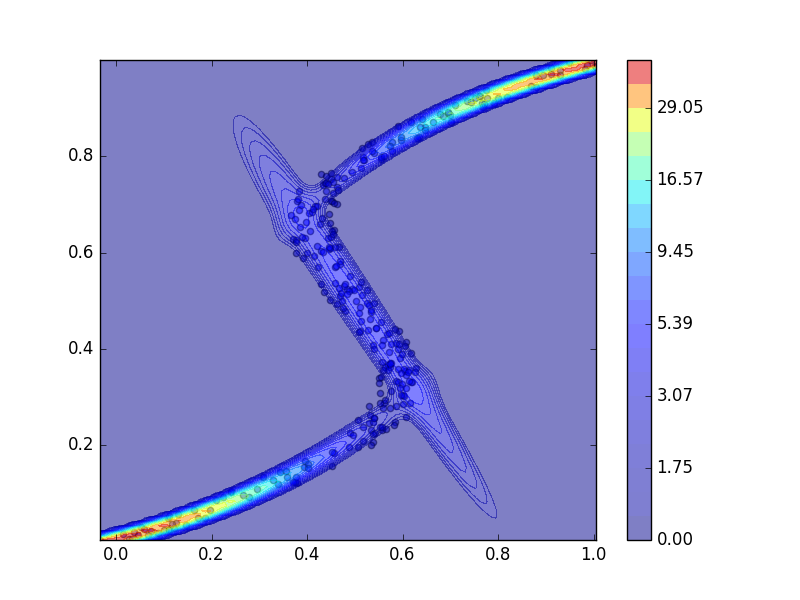
    # PRML図5.21(c)の再現
    plt.scatter(x, t, alpha=0.5, label="observation")
    levels_log = np.linspace(0, np.log(probs.max()), 21)
    levels = np.exp(levels_log)
    levels[0] = 0
    plt.contourf(X_test, Y_test, Probs, levels, alpha=0.5)
    plt.colorbar()
    plt.xlim(x.min(), x.max())
    plt.ylim(t.min(), t.max())
    plt.show()

全体のコード

3行目のneural_networkは前回実装したneural_network.pyのことです。このコードと同じディレクトリに入れて下さい。

mixture_density_network.py

import matplotlib.pyplot as plt
import numpy as np
from neural_network import TanhLayer, LinearLayer, NeuralNetwork


class GaussianMixture(object):
    """Negative Log Likelihood of Gaussian Mixture model"""
    def __init__(self, n_components):
        self.n_components = n_components

    def __call__(self, X, targets):
        sigma, weight, mu = self.activate(X)
        gauss = self.gauss(mu, sigma, targets)
        return -np.sum(np.log(np.sum(weight * gauss, axis=1)))

    def activate(self, X):
        assert np.size(X, 1) == 3 * self.n_components
        X_sigma, X_weight, X_mu = np.split(X, [self.n_components, 2 * self.n_components], axis=1)
        sigma = np.exp(X_sigma)
        weight = np.exp(X_weight - np.max(X_weight, 1, keepdims=True))
        weight /= np.sum(weight, axis=1, keepdims=True)
        return sigma, weight, X_mu

    def gauss(self, mu, sigma, targets):
        return np.exp(-0.5 * (mu - targets) ** 2 / np.square(sigma)) / np.sqrt(2 * np.pi * np.square(sigma))

    def delta(self, X, targets):
        sigma, weight, mu = self.activate(X)
        var = np.square(sigma)
        gamma = weight * self.gauss(mu, sigma, targets)
        gamma /= np.sum(gamma, axis=1, keepdims=True)

        delta_mu = gamma * (mu - targets) / var
        delta_sigma = gamma * (1 - (mu - targets) ** 2 / var)
        delta_weight = weight - gamma
        delta = np.hstack([delta_sigma, delta_weight, delta_mu])
        return delta


def create_toy_dataset(func, n=300):
    t = np.random.uniform(size=(n, 1))
    x = func(t) + np.random.uniform(-0.05, 0.05, size=(n, 1))
    return x, t


def sample(x, t, n=None):
    assert len(x) == len(t)
    N = len(x)
    if n is None:
        n = N
    indices = np.random.choice(N, n, replace=False)
    return x[indices], t[indices]


def main():

    def func(x):
        return x + 0.3 * np.sin(2 * np.pi * x)

    x, t = create_toy_dataset(func)

    layers = [TanhLayer(1, 5, std=0.1), LinearLayer(5, 9, std=0.1)]
    cost_function = GaussianMixture(3)
    nn = NeuralNetwork(layers, cost_function)
    # nn._gradient_check(np.array([[0.5]]), np.array([[0.5]]))
    learning_rate = 1e-4
    for i in xrange(500000):
        if i % 10000 == 0:
            print "step %6d, cost %f" % (i, nn.cost(x, t))
            learning_rate *= 0.9
        batch = sample(x, t, n=100)
        nn.fit(*batch, learning_rate=learning_rate)

    x_test = np.linspace(x.min(), x.max(), 100)
    y_test = np.linspace(t.min(), t.max(), 100)
    X_test, Y_test = np.meshgrid(x_test, y_test)
    test = np.array([X_test, Y_test]).transpose(1, 2, 0).reshape(-1, 2)

    sigma, weight, mu = nn(test[:, 0].reshape(-1, 1))
    probs = cost_function.gauss(mu, sigma, test[:, 1].reshape(-1, 1))
    probs = np.sum(weight * probs, axis=1)
    Probs = probs.reshape(100, 100)

    plt.plot(x_test, weight[:100, 0], color="blue")
    plt.plot(x_test, weight[:100, 1], color="red")
    plt.plot(x_test, weight[:100, 2], color="green")
    plt.title("weights")
    plt.show()

    plt.plot(x_test, mu[:100, 0], color="blue")
    plt.plot(x_test, mu[:100, 1], color="red")
    plt.plot(x_test, mu[:100, 2], color="green")
    plt.title("means")
    plt.show()

    plt.scatter(x, t, alpha=0.5, label="observation")
    levels_log = np.linspace(0, np.log(probs.max()), 21)
    levels = np.exp(levels_log)
    levels[0] = 0
    plt.contourf(X_test, Y_test, Probs, levels, alpha=0.5)
    plt.colorbar()
    plt.xlim(x.min(), x.max())
    plt.ylim(t.min(), t.max())
    plt.show()


if __name__ == '__main__':
    main()

結果

青点をトレーニングデータ点として、上のコードを走らせて混合密度ネットワークを学習させた結果、PRMLの図5.21のようなグラフの再現が出来ました。ただし、線の色などは違うことがあります。３つのガウス分布、青、赤、緑、によってトレーニングデータ点にフィッティングされています。

学習の様子

前回同様、学習の過程を動画にもしてみました。

終わりに

混合密度ネットワークというものをPRMLで読むまで聞いたことがなかったのでネットで検索してみると、PRMLの著者C・M・ビショップさんが1994年に書かれた論文がヒットしたので、この人自身が提唱したものなのかもしれません。混合密度ネットワークは多峰性のあるものなら従来のモデルより有効だと思われるので、これを何らかの実データに対して適用してみたいものです。