PRML第5章 ニューラルネットワーク Python実装

PRMLの第5章では最近流行りのニューラルネットワークが紹介されています。ニューラルネットワークを実装してみたという類のものはネット上にいくつもありますので、できる限り見慣れないものを題材にしたかったので混合密度ネットワークをほぼNumpyだけで実装することにしました。
ただ、コード分量が結構大きくなってしまったので２回に分けて、この記事では結局普通のニューラルネットワークを実装して、混合密度ネットワークは次回にします。

ニューラルネットワーク

ネットワーク構造

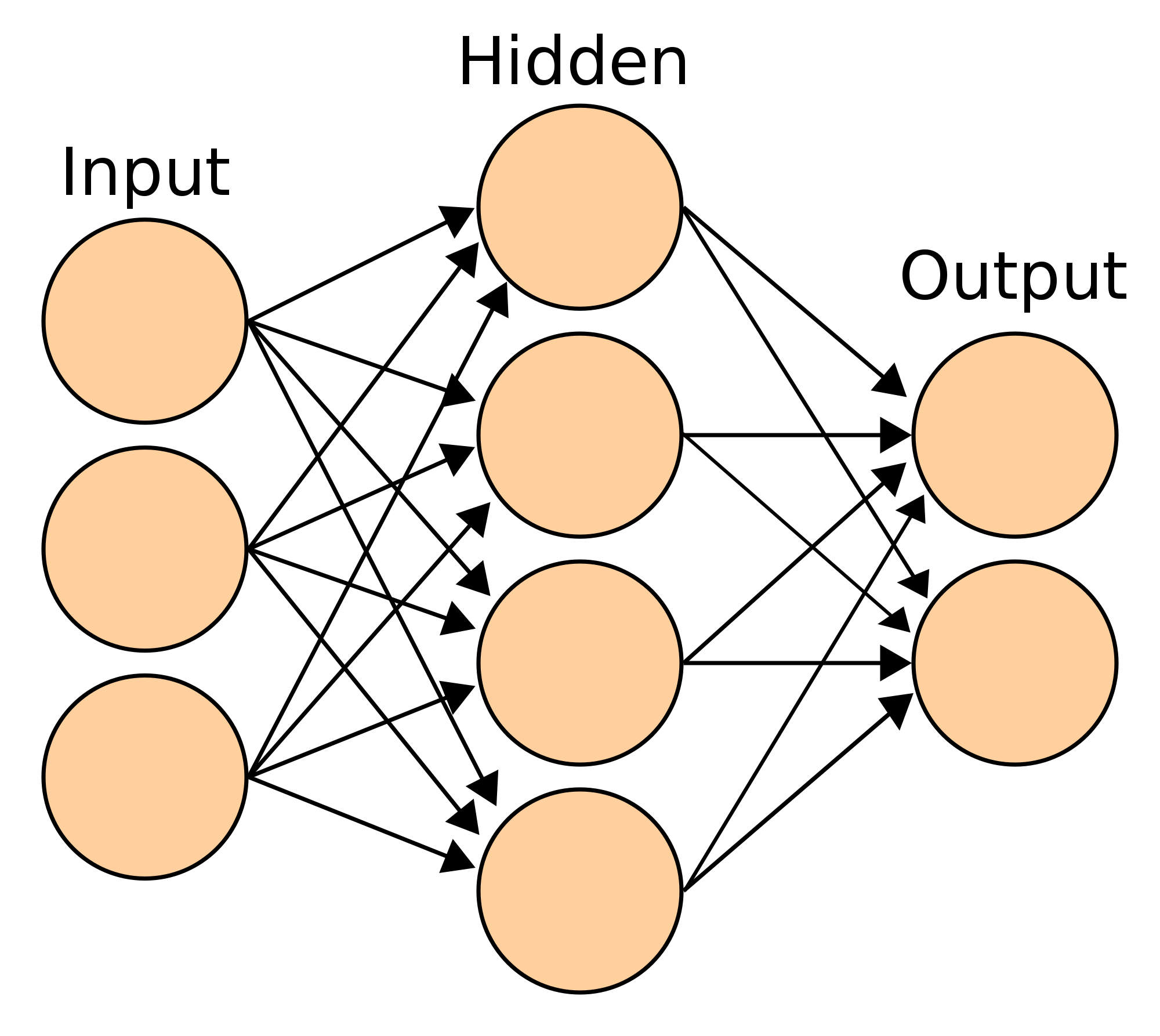
これは入力ユニットが３次元${\bf x} = (x_1,x_2,x_3)$、隠れユニットが４次元${\bf z} = (z_1,z_2,z_3,z_4)$、出力ユニットが２次元${\bf z}= (z_1,z_2)$の２層のニューラルネットワークを模式的に表した図です。入力から隠れユニットが第一層(${\bf x}\to {\bf z}$)、隠れユニットから出力が第二層(${\bf z}\to {\bf y}$)となっています。ユニットの次元、層の数などは問題に応じて変える必要があります。

順伝播

順伝播とは入力からネットワークの出力を計算するステップのことをいいます。入力${\bf x}$から隠れユニット${\bf z}$を計算して、そのあとに隠れユニット${\bf z}$から出力${\bf y}$を計算します。

第一層の隠れユニットの一つ$z_1$は、

\begin{align}
a_{z_1} &= w_{11}^{(1)}x_1+w_{12}^{(1)}x_2+w_{13}^{(1)}x_3 + b_1^{(1)}\\
z_1 &= f^{(1)}(a_{z_1})
\end{align}

と計算されます。ここで、$a_{z_1}$を1番目の隠れユニットの活性、$w_{1j}^{(1)}$をj番目の入力ユニットから1番目の隠れユニットへの重み,$b_1$は１番目の隠れユニットのバイアス、$f^{(1)}$を第一層の活性化関数としています。

これらを$z_2,z_3,z_4$についても同様の式を立てることはできますが、３つも式があるのはややこしくなっていくので、よく行列を使います。

\begin{align}
\begin{bmatrix}
a_{z_1}\\
a_{z_2}\\
a_{z_3}\\
a_{z_4}
\end{bmatrix}
&=
\begin{bmatrix}
w_{11}^{(1)} & w_{12}^{(1)} & w_{13}^{(1)}\\
w_{21}^{(1)} & w_{22}^{(1)} & w_{23}^{(1)}\\
w_{31}^{(1)} & w_{32}^{(1)} & w_{33}^{(1)}\\
w_{41}^{(1)} & w_{42}^{(1)} & w_{43}^{(1)}
\end{bmatrix}
\begin{bmatrix}
x_1\\
x_2\\
x_3
\end{bmatrix}
+
\begin{bmatrix}
b_1^{(1)}\\
b_2^{(1)}\\
b_3^{(1)}\\
b_4^{(1)}
\end{bmatrix}
\\
\begin{bmatrix}
z_1\\
z_2\\
z_3\\
z_4
\end{bmatrix}
&=
\begin{bmatrix}
f^{(1)}(a_{z_1})\\
f^{(1)}(a_{z_2})\\
f^{(1)}(a_{z_3})\\
f^{(1)}(a_{z_4})
\end{bmatrix}
\end{align}

これをもっと簡潔にして、

\begin{align}
{\bf a}_z &= W^{(1)}{\bf x} + {\bf b}^{(1)}\\
{\bf z} &= f^{(1)}({\bf a}_z)
\end{align}

とも表します。
これで第１層の順伝播ができました。

同じようにして第２層目は、

\begin{align}
{\bf a}_y &= W^{(2)}{\bf y} + {\bf b}^{(2)}\\
{\bf y} &= f^{(2)}({\bf a}_y)
\end{align}

と表せます。

ちなみに、これらをまとめると、

{\bf y} = f^{(2)}(W^{(2)}f^{(1)}(W^{(1)}{\bf x} + {\bf b}^{(1)}) + {\bf b}^{(2)})

となります。
こうして、入力から出力への計算ができます。

逆伝播

ニューラルネットワークにはパラメータが多く(今回の例だと26個)あります。これらの勾配を効率的に計算する方法が逆伝播です。
入力とそのターゲットの組$\{{\bf x}, {\bf t}\}$、と最小化したいコスト関数$E$を考えます。まず、順伝播によって入力${\bf x}$からネットワークの出力${\bf y}$を計算します。すると、コスト関数が計算でき、例えば$E=||{\bf t} - {\bf y}||^2$、そしてターゲット${\bf t}$との誤差が生じます。この誤差を入力まで伝播させていきます。
出力層での誤差、実際にはコスト関数の出力での偏微分、は

{\partial E\over\partial y_i}

です。これを用いると、${\bf a}_y$の誤差、コスト関数の${\bf a}_y$での偏微分は

\begin{align}
{\partial E\over\partial a_{y_i}} &= {\partial E\over\partial y_i}{\partial y_i\over\partial a_{y_i}}\\
&= {\partial E\over\partial y_i}f'^{(2)}(a_{y_i})\\
(&= y_i - t_i)
\end{align}

として求まります。出力層の活性化関数$f^{(2)}$が恒等写像、シグモイド関数、ソフトマックス関数などの正準連結関数であれば、${\bf a}_y$の誤差は単純に出力とターゲットの差となります。
${\bf a}_y$の誤差が求まれば第２層での重みの勾配が求まります。なぜなら、

\begin{align}
{\partial a_{y_i}\over\partial w_{ij}^{(2)}} &= z_j\\
{\partial a_{y_i}\over\partial b_i^{(2)}} &= 1
\end{align}

より、

\begin{align}
{\partial E\over\partial w_{ij}^{(2)}} &= {\partial E\over\partial a_{y_i}}{\partial a_{y_i}\over\partial w_{ij}^{(2)}}\\
&= {\partial E\over\partial a_{y_i}}z_j\\
{\partial E\over\partial b_i^{(2)}} &= {\partial E\over\partial a_{y_i}}{\partial a_{y_i}\over\partial b_i^{(2)}}\\
&= {\partial E\over\partial a_{y_i}}
\end{align}

となり、計算できます。出力の誤差を伝播させて活性${\bf a}_{y}$の誤差を求めて、その誤差を用いてパラメータの勾配を計算しました。
さらに、${\bf a}_y$の誤差が求まれば重みについての勾配だけでなく第２層の入力${\bf z}$の誤差も計算できます。

\begin{align}
{\partial E\over\partial z_j} &= \sum_{i=1}^2 {\partial E\over\partial a_{y_i}}{\partial a_{y_i}\over\partial z_j}\\
&= \sum_{i=1}^2 {\partial E\over\partial a_{y_i}}w_{ij}^{(2)}
\end{align}

こうして第２層の出力${\bf y}$から入力${\bf z}$への誤差の伝播ができました。
この第２層の入力${\bf z}$の誤差は第１層の出力の誤差でもあるので、今までのことをまた繰り返すことで、第１層の活性での誤差、重みの勾配も得られます。

\begin{align}
{\partial E\over\partial a_{z_i}} &= {\partial E\over\partial z_i}{\partial z_i\over\partial a_{z_i}}\\
&= {\partial E\over\partial z_i}f'^{(2)}(a_{z_i})\\
{\partial E\over\partial x_j} &= \sum_{i=1}^4 {\partial E\over\partial a_{z_i}}{\partial a_{z_i}\over\partial x_j}\\
&= \sum_{i=1}^4 {\partial E\over\partial a_{z_i}}w_{ij}^{(1)}\\
{\partial E\over\partial w_{ij}^{(1)}} &= {\partial E\over\partial a_{z_i}}{\partial a_{z_i}\over\partial w_{ij}^{(1)}}\\
&= {\partial E\over\partial a_{z_i}}x_j\\
{\partial E\over\partial b_i^{(1)}} &= {\partial E\over\partial a_{z_i}}{\partial a_{y_i}\over\partial b_i^{(1)}}\\
&= {\partial E\over\partial a_{z_i}}\\
\end{align}

このようにして、出力層での誤差を入力まで伝播させ、その過程で重みパラメータの更新に必要な勾配を計算できます。

逆伝播まとめ

出力ユニットでの誤差から逆向きに伝播させて

出力ユニット	第２層の活性
${\partial E\over\partial y_i}$	${\partial E\over\partial a_{y_i}}={\partial E\over\partial y_i}f'^{(2)}(a_{y_i})~~~(=y_i - t_i)$
活性での誤差からパラメータでの勾配を計算します。

\begin{align}
{\partial E\over\partial w_{ij}^{(2)}} &= {\partial E\over\partial a_{y_i}}z_j\\
{\partial E\over\partial b_i^{(2)}} &= {\partial E\over\partial a_{y_i}}
\end{align}

これを第１層にも伝播させます。

隠れユニット	第１層の活性
${\partial E\over\partial z_j}=\sum_{i=1}^2 {\partial E\over\partial a_{y_i}}w_{ij}^{(2)}$	${\partial E\over\partial a_{z_j}}={\partial E\over\partial z_j}f'^{(1)}(a_{j_1})$
そして、活性での誤差からパラメータの勾配が得られます。

\begin{align}
{\partial E\over\partial w_{ij}^{(1)}} &= {\partial E\over\partial a_{z_i}}x_j\\
{\partial E\over\partial b_i^{(1)}} &= {\partial E\over\partial a_{z_i}}
\end{align}

コード

ライブラリ

今回は重みの初期化に切断正規分布を用いるために、numpy以外のものも使いました。私が普段ニューラルネットワークを組むときはTensorflowを使っているのですが、Tensorflowでは切断正規分布をつかって重みの初期化をしているので、ここでもそれに倣うことにしました。

import numpy as np
from scipy.stats import truncnorm

層

ニューラルネットワークの一つの層を表すクラスです。インスタンスを生成するときに重みの初期化を行い、入力を入れて順伝播させたあと、誤差の逆伝播をします。このクラスをベースにして、実際にニューラルネットワークをモデルするのに使う層を組みます。

class Layer(object):

    def __init__(self, dim_input, dim_output, std=1., bias=0.):
        self.w = truncnorm(a=-2 * std, b=2 * std, scale=std).rvs((dim_input, dim_output))
        self.b = np.ones(dim_output) * bias

    def __call__(self, X):
        self.input = X
        return self.forward_propagation(X)

    def back_propagation(self, delta, learning_rate):
        # derivative with respect to activation
        delta = delta * self.activation_derivative()

        w = np.copy(self.w)
        self.w -= learning_rate * self.input.T.dot(delta)
        self.b -= learning_rate * np.sum(delta, axis=0)

        # derivative with respect to input
        return delta.dot(w.T)

Layer	説明
__init__	この層の入力と出力の次数を入れて、パラメータの初期化
__call__	この層の入力から順伝播させてこの層の出力を計算
back_propagation	この層の出力の誤差と学習係数を入れて、パラメータを更新してこの層の入力の誤差を計算

層：恒等写像

活性化関数が恒等写像$f(a)=a$の層。
順伝播の計算と活性化関数の微分を計算するメソッドを新たに定義することで層を組んでいきます。

class LinearLayer(Layer):

    def forward_propagation(self, X):
        return X.dot(self.w) + self.b

    def activation_derivative(self):
        return 1

層：ロジスティックシグモイド関数

活性化関数がロジスティックシグモイド関数$f(x)={1\over1+\exp(-x)}$の層。ロジスティックシグモイド関数の微分は$f'(x)=f(x)(1 - f(x))$となっています。

class SigmoidLayer(Layer):

    def forward_propagation(self, X):
        activation = X.dot(self.w) + self.b
        self.output = 1 / (1 + np.exp(-activation))
        return self.output

    def activation_derivative(self):
        return self.output * (1 - self.output)

この要領で他にも活性化関数に双曲線正接関数$\tanh(x)$や正規化線形関数$\max(x, 0)$を用いた層なども組むことができます。

コスト関数：二乗和誤差

回帰問題を解くときによく用いる誤差関数です。

class SumSquaresError(object):

    def activate(self, X):
        return X

    def __call__(self, X, targets):
        return 0.5 * np.sum((X - targets) ** 2)

    def delta(self, X, targets):
        return X - targets

コスト関数：シグモイドクロスエントロピー

２クラス分類をしたいときに用いる誤差関数です。ロジスティックシグモイド関数で非線形変換をしてからクロスエントロピーを計算します。

class SigmoidCrossEntropy(object):

    def activate(self, logits):
        return 1 / (1 + np.exp(-logits))

    def __call__(self, logits, targets):
        probs = self.activate(logits)
        p = np.clip(probs, 1e-10, 1 - 1e-10)
        return np.sum(-targets * np.log(p) - (1 - targets) * np.log(1 - p))

    def delta(self, logits, targets):
        probs = self.activate(logits)
        return probs - targets

この要領で、多クラス分類に用いるソフトマックスクロスエントロピーも実装しています。

ニューラルネットワーク

コスト関数に活性化関数があるので、最終層はLinearLayerを用いるようにします。有限幅の差分による近似を用いることで、誤差逆伝播が正しく実装されているのかを確認できるようにしています。

class NeuralNetwork(object):

    def __init__(self, layers, cost_function):
        self.layers = layers
        self.cost_function = cost_function

    def __call__(self, X):
        for layer in self.layers:
            X = layer(X)
        return self.cost_function.activate(X)

    def fit(self, X, t, learning_rate):
        for layer in self.layers:
            X = layer(X)

        delta = self.cost_function.delta(X, t)
        for layer in reversed(self.layers):
            delta = layer.back_propagation(delta, learning_rate)

    def cost(self, X, t):
        for layer in self.layers:
            X = layer(X)
        return self.cost_function(X, t)

    def _gradient_check(self, X=None, t=None, eps=1e-6):
        if X is None:
            X = np.array([[0.5 for _ in xrange(np.size(self.layers[0].w, 0))]])
        if t is None:
            t = np.zeros((1, np.size(self.layers[-1].w, 1)))
            t[0, 0] = 1.

        e = np.zeros_like(X)
        e[:, 0] += eps
        x_plus_e = X + e
        x_minus_e = X - e
        grad = (self.cost(x_plus_e, t) - self.cost(x_minus_e, t)) / (2 * eps)

        for layer in self.layers:
            X = layer(X)
        delta = self.cost_function.delta(X, t)
        for layer in reversed(self.layers):
            delta = layer.back_propagation(delta, 0)

        print "==================================="
        print "checking gradient"
        print "finite difference", grad
        print " back propagation", delta[0, 0]
        print "==================================="

NueralNetwork	説明
__init__	ネットワーク構造とコスト関数の定義
__call__	順伝播の計算
fit	ネットワークの学習
cost	コスト関数の値を計算
_gradient_check	逆伝播の勾配の確認

コード全体

全体のコードはこちらです。このモジュールから必要なものだけimportして、回帰や分類問題を解くコードを組みます。

neural_network.py

import numpy as np
from scipy.stats import truncnorm


class Layer(object):

    def __init__(self, dim_input, dim_output, std=1., bias=0.):
        self.w = truncnorm(a=-2 * std, b=2 * std, scale=std).rvs((dim_input, dim_output))
        self.b = np.ones(dim_output) * bias

    def __call__(self, X):
        self.input = X
        return self.forward_propagation(X)

    def back_propagation(self, delta, learning_rate):
        # derivative with respect to activation
        delta = delta * self.activation_derivative()

        w = np.copy(self.w)
        self.w -= learning_rate * self.input.T.dot(delta)
        self.b -= learning_rate * np.sum(delta, axis=0)

        # derivative with respect to input
        return delta.dot(w.T)


class LinearLayer(Layer):

    def forward_propagation(self, X):
        return X.dot(self.w) + self.b

    def activation_derivative(self):
        return 1


class SigmoidLayer(Layer):

    def forward_propagation(self, X):
        activation = X.dot(self.w) + self.b
        self.output = 1 / (1 + np.exp(-activation))
        return self.output

    def activation_derivative(self):
        return self.output * (1 - self.output)


class TanhLayer(Layer):

    def forward_propagation(self, X):
        activation = X.dot(self.w) + self.b
        self.output = np.tanh(activation)
        return self.output

    def activation_derivative(self):
        return 1 - self.output ** 2


class ReLULayer(Layer):

    def forward_propagation(self, X):
        activation = X.dot(self.w) + self.b
        self.output = activation.clip(min=0)
        return self.output

    def activation_derivative(self):
        return (self.output > 0).astype(np.float)


class SigmoidCrossEntropy(object):

    def activate(self, logits):
        return 1 / (1 + np.exp(-logits))

    def __call__(self, logits, targets):
        probs = self.activate(logits)
        p = np.clip(probs, 1e-10, 1 - 1e-10)
        return np.sum(-targets * np.log(p) - (1 - targets) * np.log(1 - p))

    def delta(self, logits, targets):
        probs = self.activate(logits)
        return probs - targets


class SoftmaxCrossEntropy(object):

    def activate(self, logits):
        a = np.exp(logits - np.max(logits, 1, keepdims=True))
        a /= np.sum(a, 1, keepdims=True)
        return a

    def __call__(self, logits, targets):
        probs = self.activate(logits)
        p = probs.clip(min=1e-10)
        return - np.sum(targets * np.log(p))

    def delta(self, logits, targets):
        probs = self.activate(logits)
        return probs - targets


class SumSquaresError(object):

    def activate(self, X):
        return X

    def __call__(self, X, targets):
        return 0.5 * np.sum((X - targets) ** 2)

    def delta(self, X, targets):
        return X - targets


class NeuralNetwork(object):

    def __init__(self, layers, cost_function):
        self.layers = layers
        self.cost_function = cost_function

    def __call__(self, X):
        for layer in self.layers:
            X = layer(X)
        return self.cost_function.activate(X)

    def fit(self, X, t, learning_rate):
        for layer in self.layers:
            X = layer(X)

        delta = self.cost_function.delta(X, t)
        for layer in reversed(self.layers):
            delta = layer.back_propagation(delta, learning_rate)

    def cost(self, X, t):
        for layer in self.layers:
            X = layer(X)
        return self.cost_function(X, t)

    def _gradient_check(self, X=None, t=None, eps=1e-6):
        if X is None:
            X = np.array([[0.5 for _ in xrange(np.size(self.layers[0].w, 0))]])
        if t is None:
            t = np.zeros((1, np.size(self.layers[-1].w, 1)))
            t[0, 0] = 1.

        e = np.zeros_like(X)
        e[:, 0] += eps
        x_plus_e = X + e
        x_minus_e = X - e
        grad = (self.cost(x_plus_e, t) - self.cost(x_minus_e, t)) / (2 * eps)

        for layer in self.layers:
            X = layer(X)
        delta = self.cost_function.delta(X, t)
        for layer in reversed(self.layers):
            delta = layer.back_propagation(delta, 0)

        print "==================================="
        print "checking gradient"
        print "finite difference", grad
        print " back propagation", delta[0, 0]
        print "==================================="

２クラス分類

上のneural_network.pyとこのファイルは同一ディレクトリに入れます。

binary_classification.py

import pylab as plt
import numpy as np
from neural_network import TanhLayer, LinearLayer, SigmoidCrossEntropy, NeuralNetwork


def create_toy_dataset():
    x = np.random.uniform(-1., 1., size=(1000, 2))
    labels = (np.prod(x, axis=1) > 0).astype(np.float)
    return x, labels.reshape(-1, 1)


def main():
    x, labels = create_toy_dataset()
    colors = ["blue", "red"]
    plt.scatter(x[:, 0], x[:, 1], c=[colors[int(label)] for label in labels])

    layers = [TanhLayer(2, 4), LinearLayer(4, 1)]
    cost_function = SigmoidCrossEntropy()
    nn = NeuralNetwork(layers, cost_function)
    nn._gradient_check()
    for i in xrange(100000):
        if i % 10000 == 0:
            print "step %6d, cost %f" % (i, nn.cost(x, labels))
        nn.fit(x, labels, learning_rate=0.001)

    X_test, Y_test = np.meshgrid(np.linspace(-1, 1, 100), np.linspace(-1, 1, 100))
    x_test = np.array([X_test, Y_test]).transpose(1, 2, 0).reshape(-1, 2)
    probs = nn(x_test)
    Probs = probs.reshape(100, 100)
    levels = np.linspace(0, 1, 11)
    plt.contourf(X_test, Y_test, Probs, levels, alpha=0.5)
    plt.colorbar()
    plt.xlim(-1, 1)
    plt.ylim(-1, 1)
    plt.show()


if __name__ == '__main__':
    main()

回帰

こちらも上のneural_network.pyと同一ディレクトリに入れます。

regression.py

import pylab as plt
import numpy as np
from neural_network import TanhLayer, LinearLayer, SumSquaresError, NeuralNetwork


def create_toy_dataset(func, n=100):
    x = np.random.uniform(size=(n, 1))
    t = func(x) + np.random.uniform(-0.1, 0.1, size=(n, 1))
    return x, t


def main():

    def func(x):
        return x + 0.3 * np.sin(2 * np.pi * x)

    x, t = create_toy_dataset(func)

    layers = [TanhLayer(1, 6, std=1., bias=-0.5), LinearLayer(6, 1, std=1., bias=0.5)]
    cost_function = SumSquaresError()
    nn = NeuralNetwork(layers, cost_function)
    nn._gradient_check()
    for i in xrange(100000):
        if i % 10000 == 0:
            print "step %6d, cost %f" % (i, nn.cost(x, t))
        nn.fit(x, t, learning_rate=0.001)

    plt.scatter(x, t, alpha=0.5, label="observation")
    x_test = np.linspace(0, 1, 1000)[:, np.newaxis]
    y = nn(x_test)
    plt.plot(x_test, func(x_test), color="blue", label="$x+0.3\sin(2\pi x)$")
    plt.plot(x_test, y, color="red", label="regression")
    plt.legend(loc="upper left")
    plt.xlabel("x")
    plt.ylabel("y")
    plt.show()


if __name__ == '__main__':
    main()

結果

２クラス分類を行うニューラルネットワークを学習させるコードを走らせると次のように出力されます。

ターミナル出力

===================================
checking gradient
finite difference 0.349788735199
 back propagation 0.349788735237
===================================

有限幅の差から計算された勾配と誤差逆伝播によって計算された誤差の値が近くなったので、実装は大丈夫そうです。

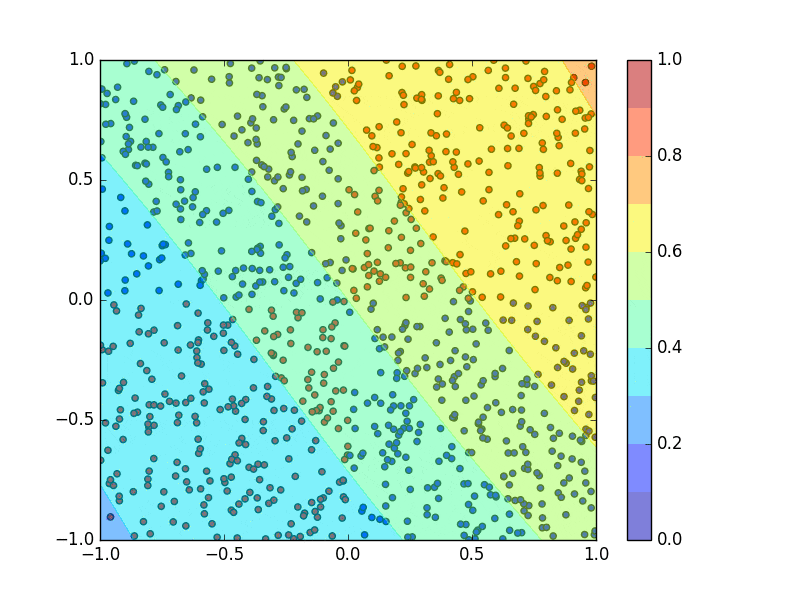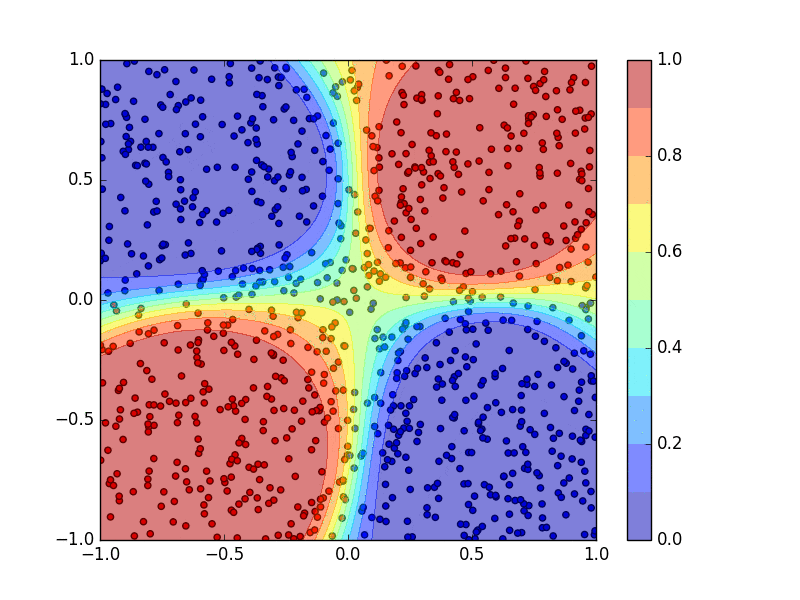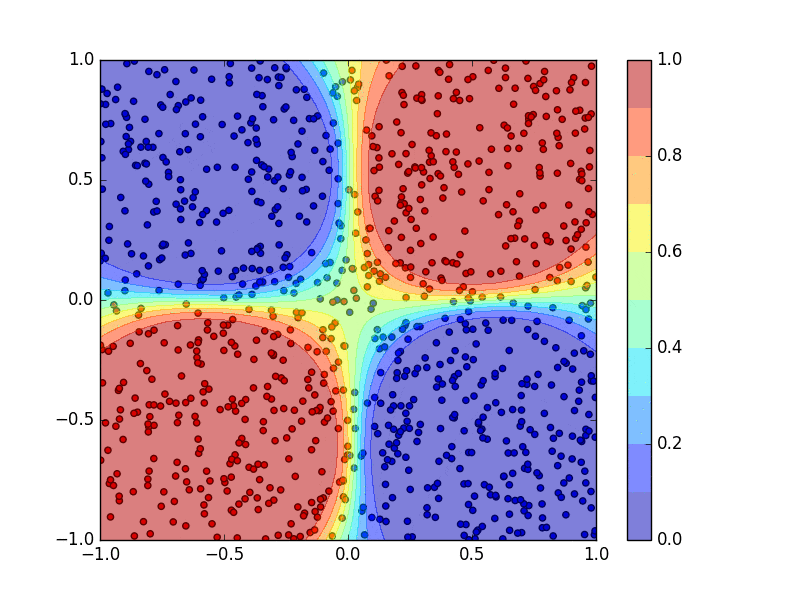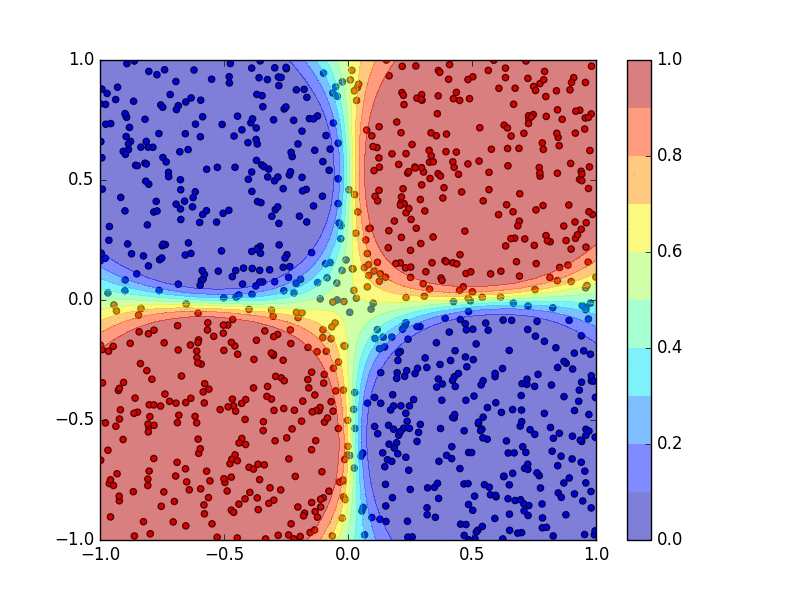
青、赤点をトレーニングデータとして２クラス分類を行うニューラルネットワークを学習させ、その出力によって２次元平面を色分けしています。ニューラルネットワークの学習の過程を動画で図示しています。(ただし、上の２クラス分類のコードは学習し終わった結果の静止画だけを表示します。)

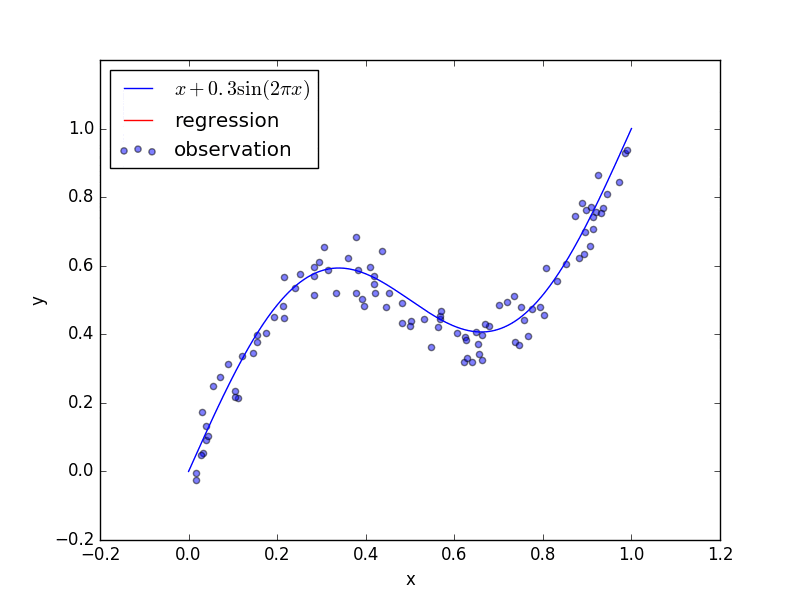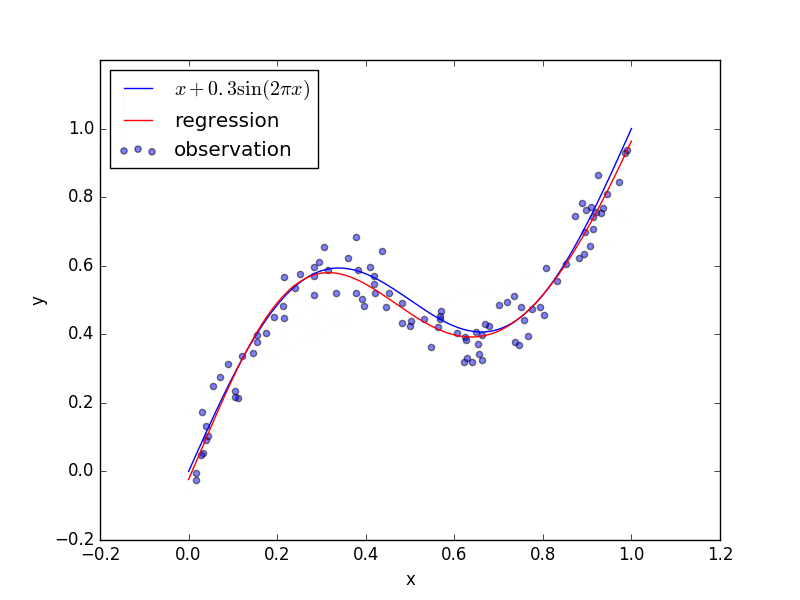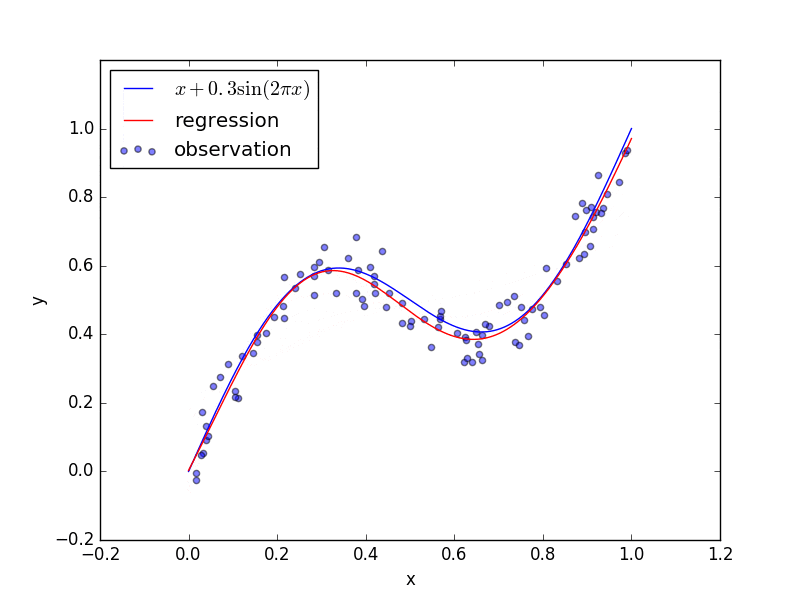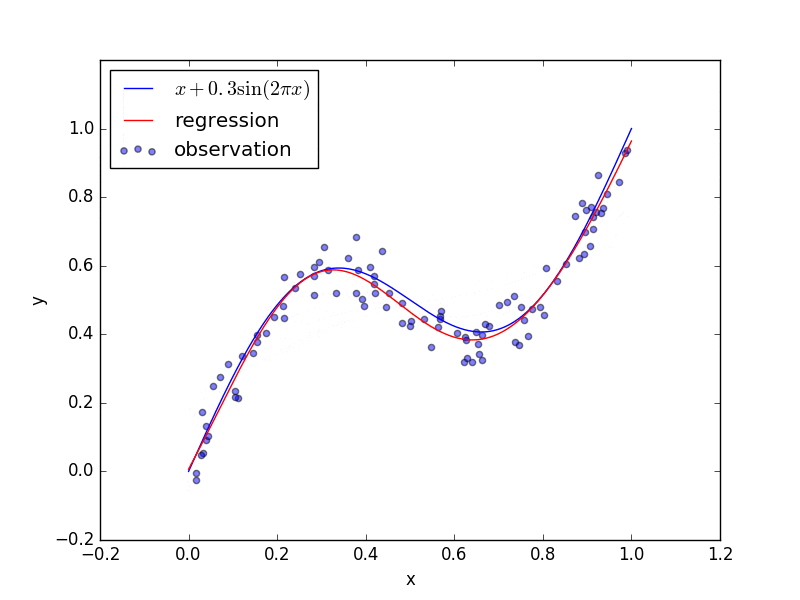
回帰にニューラルネットワークを用いたときの結果です。青点をトレーニングデータとしてニューラルネットワークを学習させて、ニューラルネットワークの出力の変化を図示しています。(ただし、上の回帰問題のコードも学習し終わった結果の静止画だけを表示します。)

終わりに

今回は、ニューラルネットワークを実装してそのトレーニングを行いました。このコードを利用して次回は混合密度ネットワークを実装します。通常のニューラルネットワークを回帰問題に使う場合、コスト関数は単峰のガウス関数をモデルにしているので、多峰の状況に対処できません。混合密度ネットワークでは混合ガウスをコスト関数に用いることでこのことを解決します。