「TensorFlowのOptimizerを比較する(ベジェ曲線編)」で、TensorFlowに提供されている6種類のOptimizerの効果を比較した。しかし、それはあくまでも補間ベジェ曲線を最適化するための特殊な場合であって、ニューラルネットワークの最適化ではない。関連性はあるにしても、直接的ではない。そこで、この記事では、TensofFlowサイトに提示されている「Deep MNIST for Experts」(mnist_expert)を使って、Deep Learningの実例に対するOptimizerの有効性を比較検討する。
この記事は、「ベジェ曲線編」の直後に書いたのだが、結果の解析が遅れていたため未公開にしていた。そのため、使用したTensorFlowのバージョンは少し古く、0.10.0rc0である。
結論
以下の結果を総合して、冒頭に結論を述べておく。
迷ったら、Adam法。但し、学習係数の値は慎重に選ぶこと
Deep MNIST for Expertsのおさらい
MNIST
MNISTは、Mixed National Institute of Staさいndards and Technologyの略称であって、手書き数字の画像を集めたデータベースである。MNISTは機械学習における「Hello World」のようなもので、多くの機械学習プラットフォームで、サンプルとして使用されている。MNISTの元サイトは、http://yann.lecun.com/exdb/mnist/ である。ここには、
- train-images-idx3-ubyte.gz
- train-labels-idx1-ubyte.gz
- t10k-images-idx3-ubyte.gz
- t10k-labels-idx1-ubyte.gz
の4個のファイルがある。それぞれ、学習用の画像と分類ラベル、テスト用の画像と分類ラベルである。画像は28x28の白黒画像であり、1pixel=1byteのバイト列として1列=784byteに格納されている。学習用は60000個、テスト用は10000個の画像が含まれている。下図は、学習用のデータのうち、最初の20画像を横に並べたものである。
ラベルデータは、以下のコード中ではサイズ=10のone-hotベクトルとして格納される。
Deep MNIST for Expertsのネットワーク構成
mnist_expertの処理の流れは、以下のようになる。分かりやすいように、8個のOPに分けて表現している。処理については、後で示すコード中の関数に対応しているが、自明な引数等を適当に省略して表現してある。shapeのうち、「?」は、同時に処理する(ミニバッチ処理)画像の枚数に対応する(枚数は可変であり、"Placeholder"に与えるデータ数によって変わる)。
| OPの名前 | 処理 | OP出力のshape | 内容 |
|---|---|---|---|
| x1 | reshape(x) | (?, 28, 28, 1) | 2次元畳み込みを行うため、4次元に変形 |
| y1 | relu(conv2d(x1, W1) + b1) | (?, 28, 28, 32) | 2次元畳み込み層 |
| x2 | max_pool_2x2(y1) | (?, 14, 14, 32) | 最大プーリング層 |
| y2 | relu(conv2d(x2, W2) + b2) | (?, 14, 14, 64) | 2次元畳み込み層 |
| x3 | reshape(max_pool_2x2(y1)) | (?, 3164) | 最大プーリング層。2次元に変形 |
| y3 | relu(matmul(x3, W3) + b3) | (?, 1024) | 大きな全結合層 |
| x4 | dropout(y3) | (?, 1024) | 過学習を避けるためのdropoutマスク |
| y4 | softmax(matmul(x4, W4) + b4) | (?, 10) | softmax回帰層。数字ごとの確率化 |
まず、2次元の畳み込みと最大プーリングを2度づつ繰り返している。両方とも畳み込みのフィルタサイズは5x5、strideは(1,1,1,1)である。ここで用いる畳み込みでは、入力側画像の枠領域を拡張してゼロをパディングする。そのため、処理の前後で画像サイズが変わらない。プーリング層は、両方共2x2のサイズであり、プーリング処理の結果、画像サイズが縦横とも半分になる。最初の畳み込みで、32個のcolor(特徴)を抽出し、2回目は64個を抽出する。2回目のプーリングの後、7x7の画像が64枚残る。これをreshapeして、7x7x64=3164のサイズの1次元に変形する。活性化関数は、ReLU関数(max(0,x))を使う。ReLU関数は、単純な割に成績が良い。
次段の全結合層は、(7x7x64+1)x1024=3212288個の大きな学習パラメータ群を含む。全結合層は、その巨大さ故に過学習が起きやすい。このため、dropout処理が行なわれる。dropout処理は、学習パラメータのうち一定の割合だけ(このコードでは50%)を適当に(おそらくランダムに)取り出し、それだけを変化させ残りは変化させない。このパターンを繰り返すことにより、一種のアンサンブル平均が行われ、過学習が抑制される。最後に、サイズ=10に帰着する線形和を行い、softmax処理を加える。softmax処理は、入力の指数を取り、その和を1になるように規格化(正規化)する。これにより、0から9までの数字に対する確率が導出される。最後段の出力y4は、教師用ラベルのone-hotベクトルと比較して交差エントロピーを計算する。こうして得られた交叉エントロピーを損失関数とし、Optimizerが最適化を行う。
Variables (学習パラメータ)
ここで用いられる学習パラメータ(最適化パラメータ)を以下に上げる。3164x1024のサイズを持つ全結合層の巨大さが目立っている。畳み込み層では、各フィルタにおける重率が全て共通であるため、パラメータの数は比較的小さい。最後段も全結合であるが、出力側のサイズが10(数字の0〜9)であるため、パラメータ数は大きくない。
| 名前 | shape | 全サイズ |
|---|---|---|
| W1 | (5, 5, 1, 32) | 800 |
| b1 | (32,) | 32 |
| W2 | (5, 5, 32, 64) | 51,200 |
| b2 | (64,) | 64 |
| W3 | (7764, 1024) | 3,211,264 |
| b3 | (1024,) | 1024 |
| W4 | (1024, 10) | 10,240 |
| b4 | (10,) | 10 |
コード
前の記事で導入したように、グラフとセッションを共用し、コードを分かりやすくするために、専用のクラスを作る。コンストラクタ中で、(データフローの)グラフの構成を登録する。以下に示すのは、mnist_expert用クラスのコンストラクタ部分である。上記で説明したOP類、Variable類が実装されている。OPのうち、その値をあとで出力する必要があるOPは、インスタンス変数(self.X)にしてある。コンストラクタの引数には、Optimizerの名前鍵と学習係数(rate)を設定する。なお、max_memoryは、GPUが同時に処理できる画像数を表している。
class TrainerExpert(Trainer):
def __init__(self, optkey, rate, max_memory=None):
Trainer.__init__(self, optkey, rate)
self.max_memory = max_memory
with self.g.as_default():
# "Placeholder"
self.x = tf.placeholder(tf.float32, shape=(None, 784)) # 画像データ
self.y = tf.placeholder(tf.float32, shape=(None, 10)) # 教師データ。One-hotベクトル
self.prob = tf.placeholder(tf.float32, shape=()) # 学習時に適用するdropoutの割合
# Variables
W1 = TrainerExpert.weight_variable((5, 5, 1, 32))
b1 = TrainerExpert.bias_variable((32,))
W2 = TrainerExpert.weight_variable((5, 5, 32, 64))
b2 = TrainerExpert.bias_variable((64,))
W3 = TrainerExpert.weight_variable((7*7*64, 1024))
b3 = TrainerExpert.bias_variable((1024,))
W4 = TrainerExpert.weight_variable((1024, 10))
b4 = TrainerExpert.bias_variable((10,))
# Operations
x1 = tf.reshape(self.x, (-1, 28, 28, 1))
y1 = tf.nn.relu(TrainerExpert.conv2d(x1, W1) + b1)
x2 = TrainerExpert.max_pool_2x2(y1)
y2 = tf.nn.relu(TrainerExpert.conv2d(x2, W2) + b2)
x3 = tf.reshape(TrainerExpert.max_pool_2x2(y2), (-1, 7*7*64))
y3 = tf.nn.relu(tf.matmul(x3, W3) + b3)
x4 = tf.nn.dropout(y3, self.prob)
self.y4 = tf.nn.softmax(tf.matmul(x4, W4) + b4)
# 交叉エントロピー
self.cross_entropy = tf.reduce_mean(
-tf.reduce_sum(self.y * tf.log(self.y4), reduction_indices=[1]))
# 学習ステップ
self.train_step = self.optimizer.minimize(self.cross_entropy)
# 確率最大のラベルが、教師用データと一致しているか
prediction = tf.equal(tf.argmax(self.y4, 1), tf.argmax(self.y, 1))
# 精度
self.accuracy = tf.reduce_mean(tf.cast(prediction, tf.float32))
# 初期化操作
self.init = tf.initialize_all_variables()
self.g.finalize()
このクラスは次のように実行する。input_dataは、tensorflowに付属しているtutorialに含まれるモジュールである。MNISTのデータを自動的にダウンロードして、メモリ上にロードする。mnistは、input_dataによってロードされたデータを処理するクラスである。mnist.train.next_batchは、学習用画像とラベルを指定した数だけ配列に入れて戻す。学習用データは60000画像あるが、過学習を避けるため、next_batchは画像をランダムに選びだす。trainer.trainは、TrainerExpertのメソッドで、学習用画像の配列と、ラベルの配列、そして、dropout関数に渡す割合を引数にとる。100回ごとに、交叉エントロピーと学習精度を出力する。
from tensorflow.examples.tutorials.mnist import input_data
import mnistlib as mnl
def do_expert(mnist, optkey, rate, loop):
trainer = mnl.TrainerExpert(optkey, rate, 1000)
trainer.initialize()
# テスト用データを用いて精度を計算する
accuracy = trainer.get_accuracy(mnist.test.images, mnist.test.labels, 1.0)
print("Step %d, accuracy= %g" % (0, accuracy))
for i in range(loop):
batch = mnist.train.next_batch(100)
trainer.train(batch[0], batch[1], 0.5)
if (i + 1)%100 == 0:
# テスト用データを用いて精度を計算する
accuracy = trainer.get_accuracy(mnist.test.images, mnist.test.labels, 1.0)
print("Step %d, accuracy= %g" % (i + 1, accuracy))
print(accuracy)
mnist = input_data.read_data_sets("data/", one_hot=True)
do_expert(mnist, 'Adam', 0.001, 10000)
検証の方法
mnist_expertに対して、次の6種類のOptimizerを比較する。比較の基準とするのは、精度である。精度は、上記のクラス中で定義したself.accuracyの値である。例えば、ある画像の正解が「7」であったとき、画像から求めた確率のうち「7」に対するものが一番大きいなら、その値は1である。もし、正解が「5」であるのに、「3」の確率が1番大きく「5」の確率が2番目なら、値は0になる。この値を、与えられた全画像に対して平均したものが精度である。
検証過程において、精度の計算に用いるデータは、学習用データではなくテスト用データでなければならない。学習用データに対して最適化が行われているのであるから、学習用データを用いて精度を計算してしまったのでは、結果が良いのは当たり前であり、参考にはならない。
ここでは、各Optimizerに対して、学習過程を10000回繰り替えして精度の変化を検証する。ミニバッチ処理のサイズは100画像とした。以下で述べるように、学習過程に偶然性が介入する。このため、各Optimizerの、各学習係数値ごとに、10回づつ試行を繰り返す。学習係数の値は、1eー5、2e-5、5e-5、0.0001、0。0002、0.0005、0.001、...、1.0、2.0、5.0、10.0のように、ファクターが1、2、5、オーダーが10^-5から10までの値について計算した。
今回の検証で得られた最も良い精度は、ほぼ99.2%である。この値は誤差に直すと0.8%であり、MNISTサイトに掲載されている各種の方法と比べても、簡単に実行できる割には良い値である。なお、MNISTサイト上で最も良い値は0.23%である。
収束過程(学習過程)と指標
ここで用いた学習方法には、以下のような偶然性(randomness)が含まれている。
- 重率とバイアスの初期値(Wn,bn)
- ミニバッチ処理による学習用データの選択抽出
- dropout関数における、変分パラメータの選択
- Optimizerにおける、変分パラメータの選択
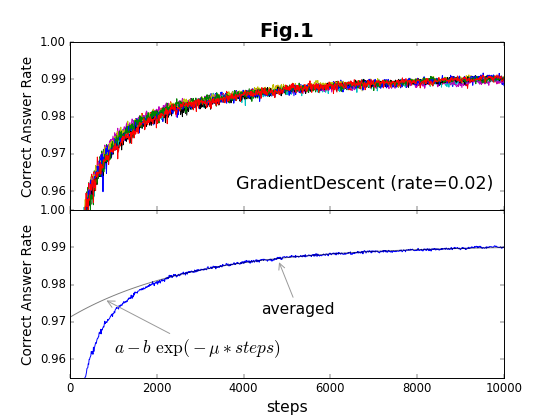
このため、同じOptimizerで同じ学習係数の値を用いても、毎回、学習結果が少しづつ異なっている。最急降下法(GradientDescent法)で学習係数が0.02の場合を例にしてみると、図1上のようになる。横軸は学習ステップ数、縦軸は精度である。これは、同じ学習過程を10回行って、その結果を重ね書きしている。精度の出力は、10ステップごとに行っている。
図1上に対して、もう少し正確な値を求めるために、以下のような操作を行う。
a. 学習、観測過程を10回くりかえす
b. それぞれの横軸をスライドさせて調整する(必要な場合)
c. 発散しているもの、および、収束過程にないものを除いて、各ステップごとに平均を取る
その結果が図1下である。かなりスムーズになっている。ところで、mnist_expertの収束過程は、次のように3段階になっているようだ。
- 初期化直後の停留過程
- 急激な収束過程
- 緩やかな漸近過程
第1段階の「初期化直後の停留過程」は、どんな場合でもあるわけではない。第1段階がある場合、初期状態によって第2段階が始まる時間(=ステップ数)が異なるため、それぞれのグラフが横方向に平行移動されたような形になる(これを解消して、平均を取るために、上記bの操作を行う)。第2段階は、第3段階に比べて、時間的には短い。このため、第3段階の漸近過程が主として収束時間を決める。漸近過程は、ほぼ指数関数的であり、以下の式で示される。
$$f(steps) = a - b\ \exp{(-\mu * steps)}$$
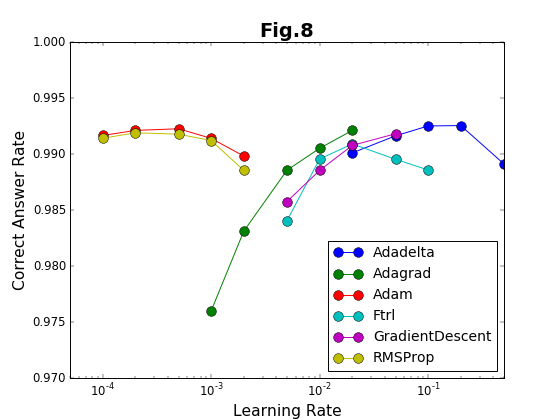
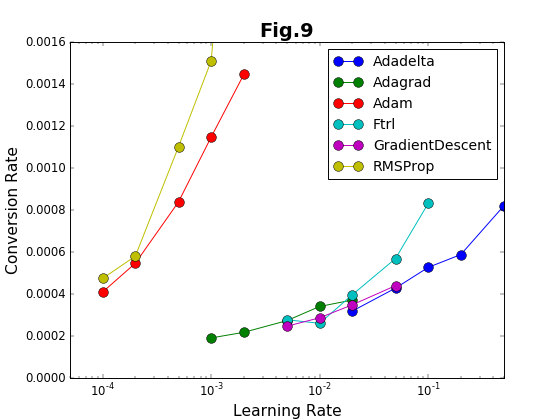
こうして得られた精度の漸近値$a$と、収束率$\mu$が、Optimizerの性能を決める指標である。漸近値が1に近いほどOptimizerの精度が良く、収束率が大きいほど効率的である。2つの指標の学習係数との関係は、それぞれ、図8と図9に示している。
発散と未収束の問題(発散、停留、破綻)
Optimizerの種類を問わず、学習係数を大きく取る方が、高い学習効率が得られ、学習精度も高くなる。しかし、前の記事でも問題になったように、学習係数の値が大きり過ぎると、学習過程が収束せずに発散してしまうという問題が生じる。そのため、学習係数を、発散しない範囲で出来るだけ大きく取るのが大切である。最も適した学習係数の値は、問題によっても異なり、Optimizerの種類によっとも異なる。ここで得られた結果は、個別の問題に応用する際の参考になるだろう。
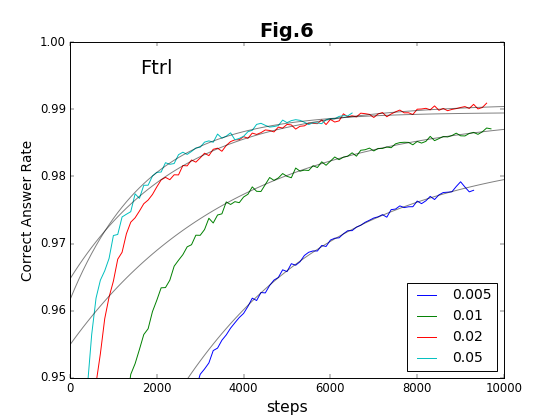
今回の結果から、発散以外に「未収束」の問題があることが分かった。未収束には、二通りがある。ひとつは、上述のように、初期状態から未収束が続く「停留」である。停留状態が継続する時間(ステップ数)は、毎回異なる。もうひとつは、収束過程にあるにも関わらず、突然、未収束の状態に戻ってしまうことである。ここでは、この現象を「発散」と区別するために「破綻」と呼ぶことにする。このような「未収束」の問題は、Ftrl法の場合に、顕著に出現する。
結果
ステップごとの精度の変化
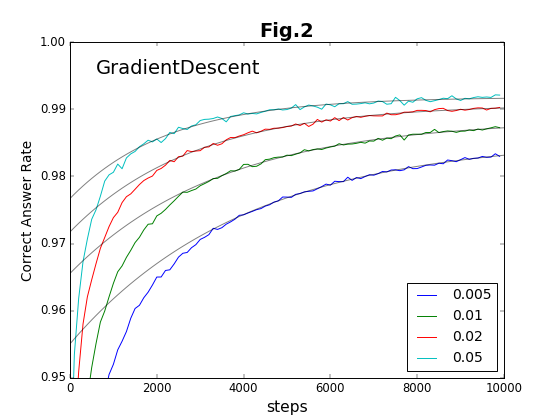
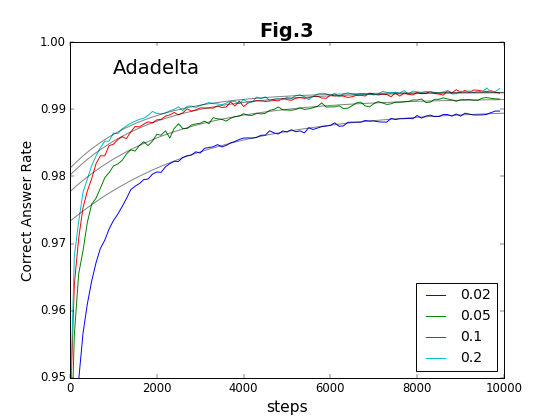
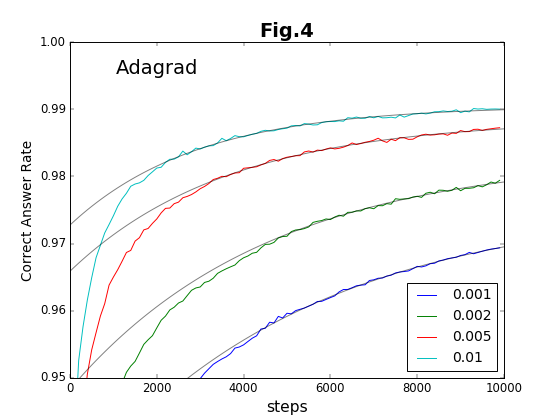
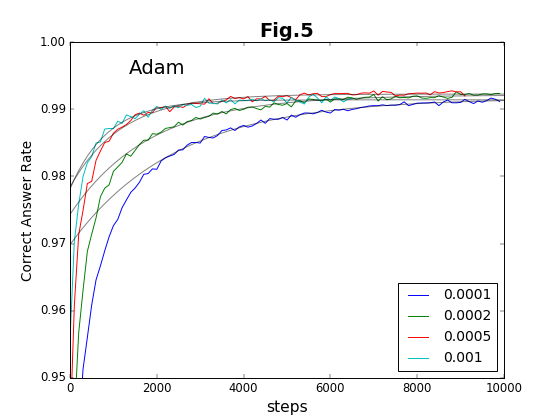
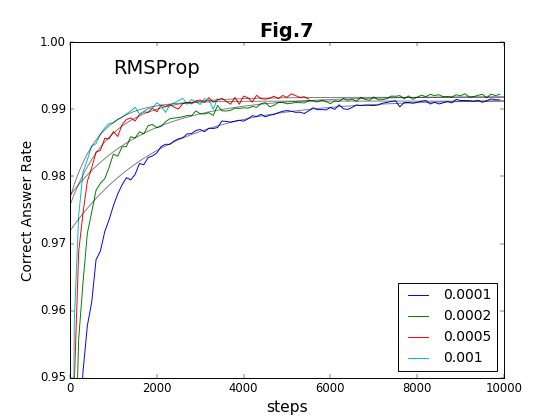
最初の6種類の方法について、学習ステップの積み重ねと精度との関係をグラフに示す(図2〜図7)。
到達最高精度と収束率
実験は10000ステップまで行っている。このステップ内で到達できる最高の精度を「到達最高精度」と名付ける。これは有限のステップで得られることを重視したもので、精度の漸近値ではない(漸近値より小さくなる)。到達最高精度を、各Optimizerごとに、学習係数の値に対してプロットしたのが図8である。学習係数は対数プロットであることに注意してほしい。
学習係数は、どの方法でも、だいたい20倍程度の範囲で有効である。その学習係数の有効範囲の様子から、Adam法とRMSProp法の組、および、それ以外の組の2種類に特徴が別れる。Adam法とRMSProp法は、到達最高精度が学習係数に対してフラットかつ高い値をキープしている。「ベジェ曲線編」でも、図19および図22の結果について推測しているのだが、Adam法とRMSProp法の収束加速アルゴリズムに類似があるのであろう。
これに対して、残りのOptimizerの中では、Adadelta法が比較的安定して精度の高い値を与えている。それ以外の方法は学習係数への依存性が強く、学習係数の最適値の範囲が狭い。
収束率(収束の速さ)を学習係数に対してプロットしたのが図9である。Adam法とRMSProp法は、収束率についても高い値を示している。
総合評価
Optimizerの性能を評価するにはまず、到達最高精度、収束率が重要である。また、一般に学習係数を大きくするほど、精度、収束率ともに向上すが、逆に、「発散」や「破綻」の可能性も大きくなる。そのため、「成功率」(有効なデータが得られる確率)も重要な要素になる。
- 到達最高精度
- 収束率
- 成功率
従って、学習係数の広い範囲で、3つの要素について良い結果を示すことが、良いOptimizerの要件である。以上を考慮して、下の表に評価を示した。上でも述べたように、Adam法、RMSProp法、Adadelta法を良い評価とした。
| Optimizer | 評価 | 最適学習係数値 | ベジェ曲線 検証1 |
ベジェ曲線 検証2 |
|---|---|---|---|---|
| GradientDescent | ○ | 0.05 | ○ | × |
| Adadelta | ◎ | 0.2 | △ | × |
| Adagrad | ○ | 0.01 | ◎ | × |
| Adam | ◎ | 0.0002 | ◎ | △ |
| Ftrl | ○ | 0.02 | ◎ | △ |
| RMSProp | ◎ | 0.0002 | △ | × |
直接Deep Learningとは関係ないが、ベジェ曲線の補完をテーマにした検証結果も併せて載せてある。
Optimizerの選択はどんな基準で選ぶべきか迷うところであるが、ここまでの検証を総合して、「迷ったらAdam法」と言うことにしたい。