インボリュート関数という関数を題材に、いろいろな方法で数値的に逆関数を作るということを行ってみたいと思います。Pythonには技術計算に使えるライブラリがたくさん揃っているので、そのライブラリを活用してそれぞれの手法の限界も見ていきたいと思います。
試してみる方法は以下の5つです。
- 多項式回帰 (scikit-learn)
- サポートベクターマシン (scikit-learn)
- Newton-Raphson法 (SciPy)
- Akimaスプライン (SciPy)
- ライブラリに頼らない実装
問題の確認
インボリュート関数とは
インボリュート関数は歯車の歯の形を決めるときに使う関数で、その定義自体は非常に簡単です。
$f(\alpha) = tan\ \alpha - \alpha$
歯車の計算をする過程でこの関数の逆関数を計算する必要があります。
逆関数とは
$inv\alpha = f(\alpha)$ が既知の時に $inv\alpha$ から逆に $\alpha$ を求める必要があるということです。
数学の記号を使えば $\alpha = f^{-1}(inv\alpha)$ と簡単に表すことができますが、実際にその計算をするのはそれほど簡単ではありません。
(注意:$inv\alpha$ は $involute(\alpha)$ の意味で使っています。invはinverseの略ではありません。)
インボリュート関数をプロットしてみる
作業はJupyter Notebookで行っていきます。
まずは必要なライブラリをインポートします。
ベクトルデータを扱うためにNumPy、プロットをするためにBokehをインポートします。
import numpy as np
from bokeh.plotting import output_notebook, figure, show
output_notebook()
インボリュート関数を定義します。
def involute_ufunc(α):
return np.tan(α) - α
ここでは、プロット作業を簡単にするためにNumPyを利用しています。
NumPyには配列(numpy.ndarray)の要素すべてに一括で関数を適用できるブロードキャストという機能があります。math.tan関数はブロードキャストに対応していないので、ブロードキャストに対応しているnumpy.tan関数を使っています。
involute_ufunc関数は引数$\alpha$で配列を受け取り、配列の要素すべてにインボリュート関数を適用して配列を返します。
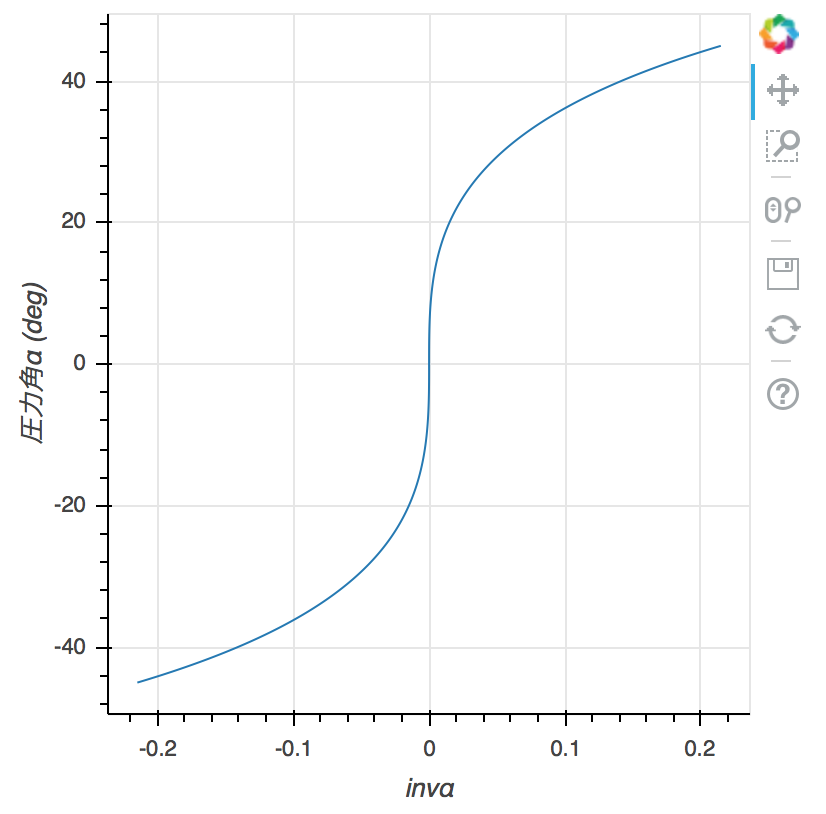
x = np.linspace(- np.pi / 4, np.pi / 4, 1000)
fig = figure(width=400, height=400)
fig.line(np.degrees(x) , involute_ufunc(x))
fig.xaxis.axis_label = '圧力角α (deg)'
fig.yaxis.axis_label = 'invα'
show(fig)

インボリュート逆関数はこれの縦軸と横軸を入れ替えたものになります。
ソースコード
説明に使ったNotebookはGistにアップロードしています。
インボリュート関数のプロット.ipynb