追記
これ以下に記述されている記述は古い内容です。
具体的には、マイナンバーの計算ロジックに一部誤りがあります。
というわけで書き直した記事へのリンクを張っておきます。
SIMD intrinsicでチェックディジットを計算してみる その2
概要
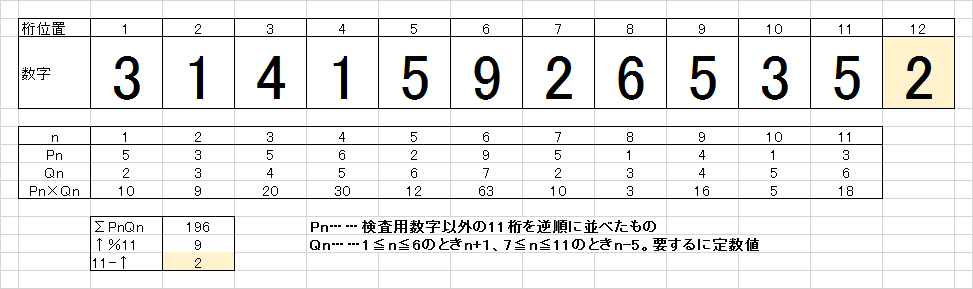
いわゆるマイナンバー(社会保障・税番号)には、その番号が真正かを判断するためのチェックディジット(検査用数字)が存在します。つまり、前11桁の数字から一意に計算される1桁の数字をもって、番号が間違っていないことを保証するのです。
計算方法については、次の画像を見れば即座に分かることでしょう。
当記事では、これをSIMD演算を投入することで高速化を狙います。
レギュレーション
C++でチェックディジットを計算する記事としては、次の2本が(たぶん)有名でしょう。
ただマイナンバー計算しても面白くないから最速を目指してみた。
C++でマイナンバーのチェックデジットを計算する
これらの記事(と言うか後者)の場合、次のようなルールでベンチマークを行っています。
- 入力はstd::stringをresize(11)した文字列
- 各桁はstd::mt19937をstd::uniform_int_distributionによって初期化
- 計算回数はとりあえず1000万回
- 出力はstd::uint8_t
- 時間計測はstd::chrono::high_resolution_clock
一見合理的に聞こえますが、毎回文字列を数字にデコードしなければならないというのは果たして、マイナンバーを計算するルーチンのベンチマークとして適切なのでしょうか。また、ベンチマーク用コードを眺める限り、文字列は各ループ毎に与えられるので、SIMD並列に向いていなさそうな雰囲気があります。
とはいえ、やるだけやってみることにしましょう。
高速化その1
std::stringの中身はchar型であり、1つ8バイトとしても11文字で88バイトしかないため、__m128i型の上に全部載ります。
なので全体を同時に掛け算した後、水平演算で合計することにより計算を行うようにします。
ただしSIMD intrinsicには8ビット毎の掛け算命令がないので、他の命令をこねくり回して表現することにします。
// 8ビット毎の掛け算命令
// http://stackoverflow.com/questions/8193601/sse-multiplication-16-x-uint8-t
__m128i mullo_epi8(__m128i a, __m128i b) noexcept(false) {
// unpack and multiply
__m128i dst_even = _mm_mullo_epi16(a, b);
__m128i dst_odd = _mm_mullo_epi16(_mm_srli_epi16(a, 8),_mm_srli_epi16(b, 8));
// repack
# ifdef __AVX2__
// only faster if have access to VPBROADCASTW
return _mm_or_si128(_mm_slli_epi16(dst_odd, 8), _mm_and_si128(dst_even, _mm_set1_epi16(0xFF)));
# else
return _mm_or_si128(_mm_slli_epi16(dst_odd, 8), _mm_srli_epi16(_mm_slli_epi16(dst_even,8), 8));
# endif
}
// 検査用数字を計算
std::uint8_t calc_check_digit_ysrken(const std::string& str) noexcept(false) {
// 自分で作った文字列に対して入力チェックが必要なのかしら……?
if (11 != str.size()) throw std::runtime_error("str.digit must be 11");
for(auto e : str) if(e < '0' || '9' < e) { throw std::runtime_error("in function calc_check_digit_ysrken : iregal charactor detect.(" + str + ')'); }
// __m128i型にマッピングし、'0'でマイナスすることで整数化する
// 必然的に後ろ8ビット×5個=40ビット分はゴミが入ることになる
__m128i p_n = _mm_loadu_si128(reinterpret_cast<const __m128i*>(str.c_str()));
static const __m128i sub = _mm_set_epi8('0','0','0','0','0','0','0','0','0','0','0','0','0','0','0','0');
p_n = _mm_sub_epi8(p_n, sub);
// q_nはどうせ定数なので決め打ちする
// p_nは反転処理すらしてないので注意
static const __m128i q_n = _mm_set_epi8(0,0,0,0,0,2,3,4,5,6,7,2,3,4,5,6);
// p_nとq_nとの掛け算
const __m128i mul_pq = mullo_epi8(p_n, q_n);
// storeして総和を計算する
static __attribute__ ((aligned(16))) unsigned char u8[16];
_mm_store_si128(reinterpret_cast<__m128i*>(u8), mul_pq);
return 11 - ((u8[0] + u8[1] + u8[2] + u8[3] + u8[4] + u8[5] + u8[6] + u8[7] + u8[8] + u8[9] + u8[10]) % 11);
}
こうして書いたコードでベンチマークしたところ、次のテスト結果(Wandbox)が得られました(10回試行した中の相加平均)。
| 種類 | [ms] |
|---|---|
| none | 669.0 |
| ryogaelbtn | 779.4 |
| yumetodo | 933.7 |
| ysrken | 782.7 |
ここでdigit_noneでは、「文字列長と文字種チェックしかしてない」ダミーコードです。この時点でチェック部分の方がよっぽど処理が重いのですが、それを見なかったことにしてグラフにするとこんな感じです。
この時点でryogaelbtn並なのですが、どうにも物足りないですよね?
高速化その2
そこで、Visual Studio 2017のプロファイラに掛けてチェックすることにしました。
1ソースだけだし楽勝かと思いきや、uniform_int_distributionがcharやuint8_t未対応とかアラインメント宣言用の構文が違うので書き換え必須といった罠を踏みましたが、とりあえず移植に成功。
すると、どうも剰余演算が遅いんじゃないかという話に……。
ここで$P_n$も$Q_n$も0以上9以下の整数ですので、$P_nQ_n$は0以上81以下の整数になります。
つまりその総和は高々$81×11=891$であり、結果をchar配列として保持しても1kB未満しか食いません。
というわけで最終行だけそうするように書き換えたところ、次のような結果になりました。
| 種類 | [ms] |
|---|---|
| none | 681.2 |
| ryogaelbtn | 795.3 |
| yumetodo | 933.6 |
| ysrken | 790.7 |
noneなどが多少揺らいでいるのはご愛嬌。引き算するとこうなりましたので、ryogaelbtnより僅かに速くなっていることは分かるかと思います。
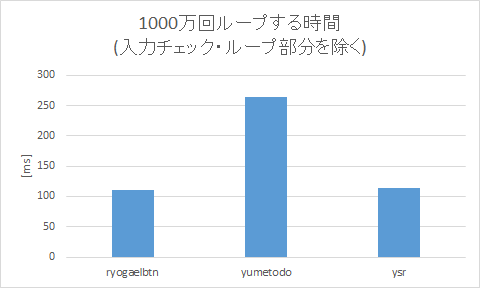
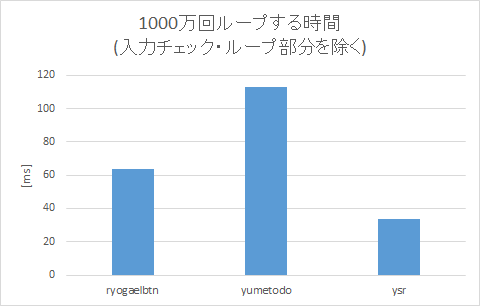
また、上記のようにVS2017上でx64ビルドすると、PCの性能(i7-4790K)とSSE2の効きがいいのか次のような結果になりました。
| 種類 | [ms] |
|---|---|
| none | 117.4 |
| ryogaelbtn | 180.8 |
| yumetodo | 230.5 |
| ysrken | 151.0 |
高速化その2.5
上記コードでは、「__m128i型をcharで区切ったものをstoreして総和を取る」操作をしています。
しかしstoreは元来重い操作なので悩ましいところ、より効率的な方法があるとの指摘をいただきました。
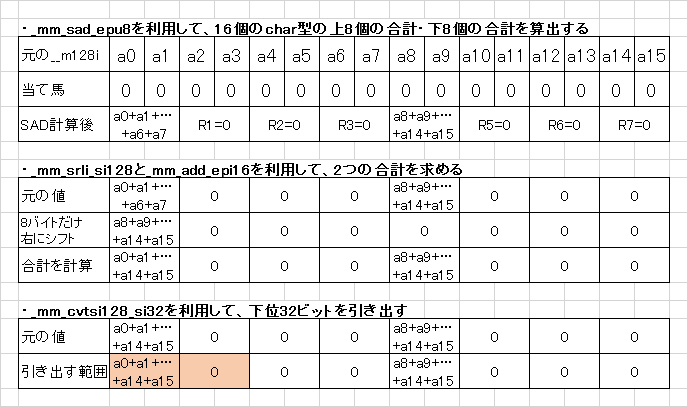
- まず、_mm_sad_epu8を利用して、16個のchar型の上8個の合計・下8個の合計を算出する
- 次に、_mm_srli_si128と_mm_add_epi16を利用して、2つの合計を求める
- 最後に、_mm_cvtsi128_si32を利用して、下位32ビットを引き出す
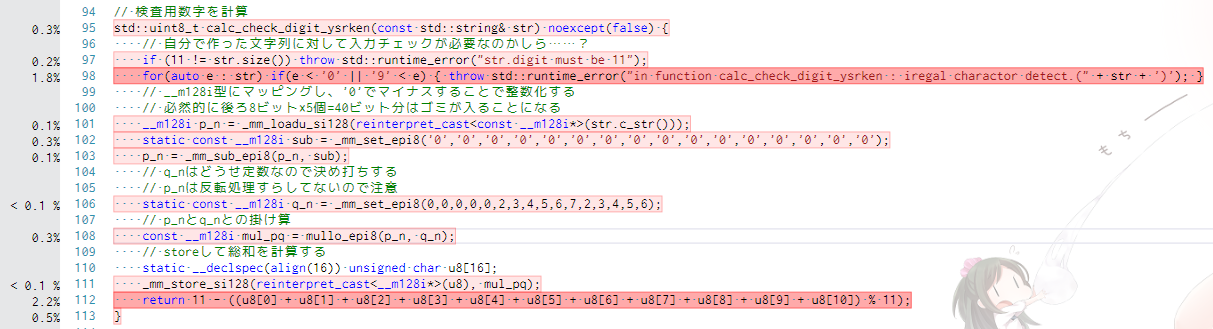
上記まで組み込んだ結果のコードは次の通り。
// 検査用数字を計算
std::uint8_t calc_check_digit_ysrken(const std::string& str) noexcept(false) {
// 自分で作った文字列に対して入力チェックが必要なのかしら……?
if (11 != str.size()) throw std::runtime_error("str.digit must be 11");
for(auto e : str) if(e < '0' || '9' < e) { throw std::runtime_error("in function calc_check_digit_ysrken : iregal charactor detect.(" + str + ')'); }
// __m128i型にマッピングし、'0'でマイナスすることで整数化する
// 必然的に後ろ8ビット×5個=40ビット分はゴミが入ることになる
__m128i p_n = _mm_loadu_si128(reinterpret_cast<const __m128i*>(str.c_str()));
static const __m128i sub = _mm_set_epi8('0','0','0','0','0','0','0','0','0','0','0','0','0','0','0','0');
p_n = _mm_sub_epi8(p_n, sub);
// q_nはどうせ定数なので決め打ちする
// p_nは反転処理すらしてないので注意
static const __m128i q_n = _mm_set_epi8(0,0,0,0,0,2,3,4,5,6,7,2,3,4,5,6);
// p_nとq_nとの掛け算
const __m128i mul_pq = mullo_epi8(p_n, q_n);
// 総和を計算する
__m128i y = _mm_sad_epu8(mul_pq, _mm_setzero_si128());
y = _mm_add_epi16(y, _mm_srli_si128(y, 8));
return g_table[_mm_cvtsi128_si32(y)];
}
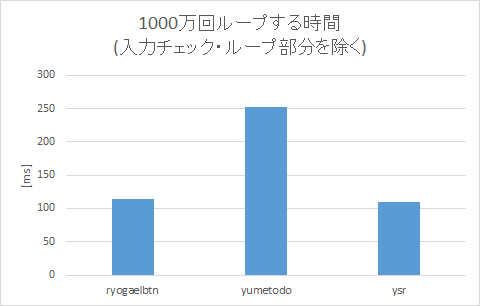
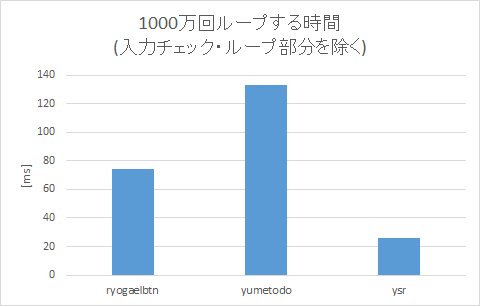
またベンチ結果も良好で、VS2017上でx64ビルドした結果、次のようになりました。
高速化その3
先ほども書きましたように、$\sum P_nQ_n$は高々891しかとりませんので、__m128i型や__m256i型を16バイトづつ使う=8並列 or 16並列で計算可能です。とりあえず8並列させるように書くとこんな感じ。
// 検査用数字を計算(8並列)
std::uint8_t calc_check_digit_ysrken2(
const std::string& str1, const std::string& str2,
const std::string& str3, const std::string& str4,
const std::string& str5, const std::string& str6,
const std::string& str7, const std::string& str8
) noexcept(false) {
// 面倒なので入力チェックは省略
// __m128i型にマッピング
__m128i p_n[11];
for (size_t i = 0; i < 11; ++i) {
p_n[i] = _mm_set_epi16(
str1[i] - '0', str2[i] - '0', str3[i] - '0', str4[i] - '0',
str5[i] - '0', str6[i] - '0', str7[i] - '0', str8[i] - '0'
);
}
// q_nはどうせ定数なので決め打ちする
static const __m128i q_n[11] = {
_mm_set1_epi16(2), _mm_set1_epi16(3), _mm_set1_epi16(4), _mm_set1_epi16(5),
_mm_set1_epi16(6), _mm_set1_epi16(7), _mm_set1_epi16(2), _mm_set1_epi16(3),
_mm_set1_epi16(4), _mm_set1_epi16(5), _mm_set1_epi16(6) };
// p_nとq_nとの掛け算
for (size_t i = 0; i < 11; ++i) {
p_n[i] = _mm_mullo_epi16(p_n[i], q_n[i]);
}
// 総和を計算する
__m128i sum = _mm_setzero_si128();
for (size_t i = 0; i < 11; ++i) {
sum = _mm_add_epi16(sum, p_n[i]);
}
// ストアしてテーブル参照
static __declspec(align(16)) unsigned short u16[8];
_mm_store_si128(reinterpret_cast<__m128i*>(u16), sum);
uint8_t result[8];
for (size_t i = 0; i < 8; ++i) {
result[i] = g_table[u16[i]];
}
return result[0]; //仮の返り値
}
で、前述の「上記のようにVS2017上でx64ビルドすると~」と同様の条件でベンチすると、noneの結果を差し引いて「1000万回で1並列あたり89.55[ms]」という結果になりました。……「高速化その2」の自コード(テーブル引きした奴)より倍近く遅くなっているのは、プロファイラによると**「p_n[i] = _mm_set_epi16(略);」が重い**とのこと。
まとめ
そこまで速くならないだろうとは思っていましたが、それでも「高速化その2」では従来法を倍近く上回る速度を叩き出しました。
また、並列化の方法を変えると却って遅くなってしまったのが興味深いところです。