ラテン超方格サンプリング(LHS)とは
多変数の層別サンプリング手法のひとつであり,n個の実験数を指定した場合，各変数をn個の区間に分割し,区間からランダムに値を取りだしランダムに組み合わせていく実験計画法である.
文章だとよくわからないのでpyDOEなるモジュールがあったので試してみる.
インストール
pip install pyDOE
実験数5個、変数2個で区間の中心を取り出す場合の実験パターンは？
>from pyDOE import lhs
>lhs(2,5,"c")
array([[ 0.3, 0.7],
[ 0.1, 0.1],
[ 0.5, 0.9],
[ 0.9, 0.5],
[ 0.7, 0.3]])
上記を再び実行すると組み合わせが異なる.
さらに引数"c"を指定しなければ区間内からランダムに抽出される.
こんな感じである.
OpenMDAOを用いた放物面のラテン超方格サンプリング
\begin{align}
& f(x,y) = (x-3)^2 + xy + (y+4)^2 - 3 \\
{\rm subject \: to} \: \: \:& -50.0\leq x \leq 50.0 \\
& -50.0\leq y \leq 50.0
\end{align}
Componentの準備
下記のparaboloid.pyファイルを準備する
paraboloid.py
from openmdao.api import Component
class Paraboloid(Component):
""" Evaluates the equation f(x,y) = (x-3)^2 + xy + (y+4)^2 - 3 """
def __init__(self):
super(Paraboloid, self).__init__()
self.add_param('x', val=0.0)
self.add_param('y', val=0.0)
self.add_output('f_xy', shape=1)
def solve_nonlinear(self, params, unknowns, resids):
"""f(x,y) = (x-3)^2 + xy + (y+4)^2 - 3 """
x = params['x']; y = params['y']
unknowns['f_xy'] = (x-3.0)**2 + x*y + (y+4.0)**2 - 3.0
Problem(問題）の設定
下記をdoe_paraboloid.pyを準備する.OpenMDAOで放物面の最小化問題を解くとの違いを後ろで概説する.
doe_paraboloid.py
#!/bin/pyhton
from openmdao.api import IndepVarComp, Group, Problem, SqliteRecorder
from paraboloid import Paraboloid
from openmdao.drivers.latinhypercube_driver import OptimizedLatinHypercubeDriver
from openmdao.core.mpi_wrap import MPI
if MPI: # pragma: no cover
# if you called this script with 'mpirun', then use the petsc data passing
from openmdao.core.petsc_impl import PetscImpl as impl
else:
# if you didn't use `mpirun`, then use the numpy data passing
from openmdao.api import BasicImpl as impl
top = Problem(impl=impl)
root = top.root = Group()
root.add('p1', IndepVarComp('x', 50.0), promotes=['x'])
root.add('p2', IndepVarComp('y', 50.0), promotes=['y'])
root.add('comp', Paraboloid(), promotes=['x', 'y', 'f_xy'])
top.driver = OptimizedLatinHypercubeDriver(num_samples=100, seed=0, population=20, \
generations=4, norm_method=2, num_par_doe=5)
top.driver.add_desvar('x', lower=-50.0, upper=50.0)
top.driver.add_desvar('y', lower=-50.0, upper=50.0)
doe_paraboloid.py続き
top.driver.add_objective('f_xy')
recorder = SqliteRecorder('doe_paraboloid')
recorder.options['record_params'] = True
recorder.options['record_unknowns'] = True
recorder.options['record_resids'] = False
top.driver.add_recorder(recorder)
top.setup()
top.run()
top.cleanup()
rootにParaboloid()をaddする際,promotesを引数にすることで,p1.xとcomp.xなどを自動接続を行っている.
今回はLHSの実験点の配置をGAを使っていい感じにしてくれるdriverであるOptimizedLatinHypercubeDriverを使用.
OptimizedLatinHypercubeDriverの引数にはサンプル数は100,ランダムシード0, GAの個体20,世代4,GAの中で各DOEポイント間の距離を正規化するノルム(np.linalg.normで使用),num_par_doeで並列化数が指定されている.
ターミナルで下記を実行する
mpirun -np 5 python doe_paraboloid.py
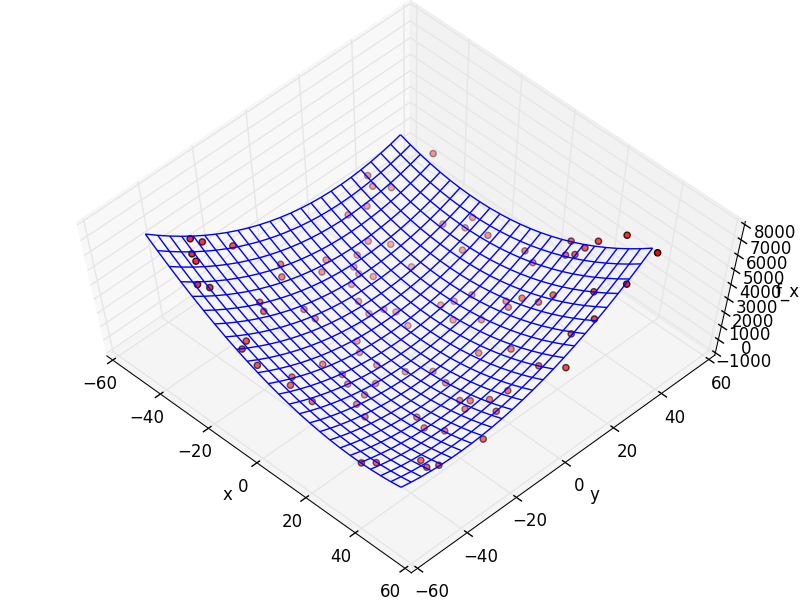
結果の読み込み
IPython
import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import sqlitedict
db =sqlitedict.SqliteDict("doe_paraboloid","iterations")
res = np.array([[0.,0.,0.]] * len(db.items()))
for i, v in enumerate(db.items()):
res[i,0] = v[1]["Unknowns"]["x"]
res[i,1] = v[1]["Unknowns"]["y"]
res[i,2] = v[1]["Unknowns"]["f_xy"]
x = np.arange(-50, 50, 4)
y = np.arange(-50, 50, 4)
X, Y = np.meshgrid(x, y)
Z = (X-3.0)**2 + X*Y + (Y+4.0)**2 - 3.0
fig = plt.figure()
ax = Axes3D(fig)
ax.plot_wireframe(X,Y,Z)
ax.scatter3D(res[:,0],res[:,1],res[:,2],c="r", marker="o")
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('f_xy')
plt.show()
