放物面の最小化問題
下記の最小化問題をOpenMDAOを使って解く.
\begin{align}
{\rm min} \: \: \:& f(x,y) = (x-3)^2 + xy + (y+4)^2 - 3 \\
\\
{\rm subject \: to} \: \: \:& -50.0\leq x \leq 50.0 \\
& -50.0\leq y \leq 50.0 \\
\\
{\rm answer} \: \: \: & f(x,y)=-27.333 \: \: {\rm at}\: x=6.667, \: y=-7.333 \\
\\
\end{align}
Componentの準備
下記のようなComponent Classを継承したParaboloid Classを定義する.
from openmdao.api import Component
class Paraboloid(Component):
""" Evaluates the equation f(x,y) = (x-3)^2 + xy + (y+4)^2 - 3 """
def __init__(self):
super(Paraboloid, self).__init__()
self.add_param('x', val=0.0)
self.add_param('y', val=0.0)
self.add_output('f_xy', shape=1)
def solve_nonlinear(self, params, unknowns, resids):
"""f(x,y) = (x-3)^2 + xy + (y+4)^2 - 3
"""
x = params['x']; y = params['y']
unknowns['f_xy'] = (x-3.0)**2 + x*y + (y+4.0)**2 - 3.0
def linearize(self, params, unknowns, resids):
""" Jacobian for our paraboloid."""
x = params['x']; y = params['y']
J = {}
J['f_xy', 'x'] = 2.0*x - 6.0 + y
J['f_xy', 'y'] = 2.0*y + 8.0 + x
return J
__init__メソッドで, 初期値0.0のx,yの入力変数を追加.
shape=1 (数値型)の未知の出力変数f_xyを定義.
solve_nonlinearメソッドで$f(x,y)$の計算を行っている.ただし計算に使用するx,yは,引数のparamsという辞書で引き渡された値を使い,同じく引数のunknowns辞書の中身を更新している
linearizeメソッドは無くても計算可能.ヤコビ行列に相当する辞書を返している.
J['f_xy', 'x']は$\frac{\partial f(x,y)}{\partial x}$の実際の計算である.
Problem(問題)の設定
Paraboloidは$f(x,y)$関数を表す部品(クラス)である.
最適化を行うためには,設計変数や目的関数を最適化手法を決める必要がある.
paraboloid.pyを保存したディレクトリで下記のコードをスクリプトもしくはインタプリタで実行する
from __future__ import print_function
from openmdao.api import IndepVarComp, Component, Problem, Group, SqliteRecorder
from openmdao.api import ScipyOptimizer
from paraboloid import Paraboloid
top = Problem()
root = top.root = Group()
root.add('p1', IndepVarComp('x', 13.0))
root.add('p2', IndepVarComp('y', -14.0))
root.add('p', Paraboloid())
root.connect('p1.x', 'p.x')
root.connect('p2.y', 'p.y')
top.driver = ScipyOptimizer()
top.driver.options['optimizer'] = 'SLSQP'
top.driver.add_desvar('p1.x', lower=-50, upper=50)
top.driver.add_desvar('p2.y', lower=-50, upper=50)
top.driver.add_objective('p.f_xy')
recorder = SqliteRecorder('paraboloid')
recorder.options['record_params'] = True
recorder.options['record_metadata'] = True
top.driver.add_recorder(recorder)
top.setup()
top.run()
top.cleanup()
print('Minimum of %f found at (%f, %f)' % (top['p.f_xy'], top['p.x'], top['p.y']))
まず1~4行目で必要なクラスをインポートしている
6行目でtopという問題(Problemのインスタンス)を定義している.文字通りの今回の最適化問題のtopである.
7行目でtopという問題のrootに新規グループを作っている.
9,10行目で変数xやyを持つp1,p2のComponent(IndepVarComp)を追加している.
このp1.x,p2.yが自由な値を取りうる本問題(top)の設計変数となる.
11行目で,pという名前のParaboloidインスタンスをrootに追加している.
12,13行目で設計変数p1.x,p2.yをParaboloidの入力変数p.x,p.yに接続している.
これにより設計変数をp1.x,p2.yを変化させれば,Paraboloidの出力変数p.f_xyも変化する.
15行目top.driver = ScipyOptimizer()以降では最適化手法について定義している.
15行目で最適化ドライバにScipyOptimizerを指定している.scipyで実装されている各最適化手法が使用できる.
16行目で最適化手法をSLSQP.逐次二次計画法である.
17,18行目では設計変数p1.x,p2.yの取りうる範囲を設定している.
そして19行目で目的関数にaraboloidの出力変数p.f_xyを指定してる.
21~24行目は、driverの運転を記録するrecorderの設定である.
21行目SqliteRecorderの引数は記録したデータの保存ファイルである.
26行目で問題(top Problem)のsetupを,27行目で最適化を実行し,28行目で後片付けをしている.
最適化結果
下記のような実行結果が表示される.
Optimization terminated successfully. (Exit mode 0)
Current function value: [-27.33333329]
Iterations: 4
Function evaluations: 5
Gradient evaluations: 4
Optimization Complete
Minimum of -27.333333 found at (6.666856, -7.333543)
次にSqliteRecorderで記録した運転記録(ファイル名:paraboloid)を読み込む.
インタプリタ上で以下のコードを実行.
import numpy as np
from matplotlib import pyplot as plt
import sqlitedict
db =sqlitedict.SqliteDict("paraboloid","iterations")
a = np.zeros(5)
for i in range(0,5):
a[i] = db[db.keys()[i]]["Unknowns"]["p.f_xy"]
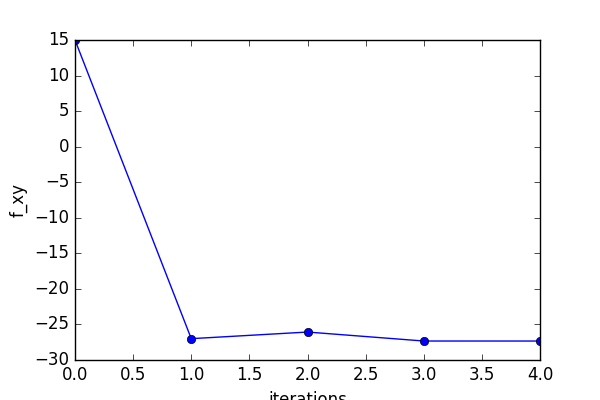
plt.plot(np.arange(0,5,1),a,"-o")
plt.xlabel("iterations")
plt.ylabel("f_xy")
plt.show()