PRML第7章 回帰問題に対する関連ベクトルマシン Python実装

今回は関連ベクトルマシンを実装しました。サポートベクトルマシンに比べてあまり有名ではありませんが、出力の値が確率になっているなど利点もあるみたいです。scikit-learn（機械学習の手法を実装しているライブラリ）にあれば多くの人が使うようになると思うのですが、Microsoftが特許を持っているから実装しなかったとかなんとか。

関連ベクトルマシン

第７章は「疎な解を持つカーネルマシン」となっていますが、関連ベクトルマシンの議論は概ねカーネル法を使わずとも成り立つ話です。線形回帰などでパラメータ${\bf w}$の事前分布を$p({\bf w}|\alpha)=\mathcal{N}({\bf w}|{\bf 0},\alpha^{-1}I)$として、一つの超パラメータ$\alpha$を設定しましたが、これを

p({\bf w}|{\bf \alpha}) = \prod_i\mathcal{N}(w_i|0,\alpha_i^{-1})

として一つ一つのパラメータごとに超パラメータを導入します。
そうしてから、第３章のエビデンス近似と同じ要領で超パラメータ${\bf\alpha}$を推定するというものです。推定された$\alpha$は無限大になる成分が多くなります。ということはパラメータ$w$の分散$\alpha^{-1}$は０に近くなり、パラメータ$w$は最初に設定した事前分布の平均0で急峻な分布になります。パラメータ$w$の値が疎になって、関連度の大きい特徴を自動で選択します（関連度自動決定）。

回帰問題に対する関連ベクトルマシン

N個の学習データ$\{x_n, t_n\}_{n=1}^N$が観測されたときの重みパラメータ${\bf w}$についての尤度関数は、

\begin{align}
p({\bf t}|{\bf\Phi},{\bf w},\beta) &= \prod_{n=1}^N p(t_n|\phi(x_n),{\bf w}, \beta)\\
&= \prod_{n=1}^N \mathcal{N}(t_n|{\bf w}^{\rm T}\phi(x_n), \beta^{-1})
\end{align}

ただし、${\bf t}=(t_1,\dots,t_N)^{\rm T}$、$\phi(\cdot)$は以下のような学習データ点を中心としたガウス関数を用いた特徴ベクトル、

\phi(x) =
\begin{bmatrix}
\phi_1(x)\\
\vdots\\
\phi_N(x)
\end{bmatrix}
=
\begin{bmatrix}
a\exp(-b(x - x_1)^2)\\
\vdots\\
a\exp(-b(x-x_N)^2)
\end{bmatrix}、

${\bf\Phi}$は要素が$\Phi_{ni}=\phi_i(x_n)$である$N\times N$の計画行列である。
重みパラメータ${\bf w}$の事後分布は、事前分布として$p({\bf w}|{\bf\alpha})$を用いると、ベイズの定理より以下のようになる。

p({\bf w}|{\bf t},{\bf\Phi},{\bf\alpha},\beta) = \mathcal{N}({\bf w}|{\bf m},{\bf \Sigma})

ただし、平均、共分散は

\begin{align}
{\bf m} &= \beta{\bf\Sigma}{\bf\Phi}^{\rm T}{\bf t}\\
{\bf\Sigma} &= \left({\bf A} + \beta{\bf\Phi}^{\rm T}{\bf\Phi}\right)^{-1}
\end{align}

行列${\bf A}$は要素が$A_{ii}=\alpha_i$の対角行列としている。

ここまでの議論を踏まえて、超パラメータ${\bf\alpha},\beta$の最尤推定を行う。対数エビデンス関数は、${\bf C} = \beta^{-1}{\bf I} + {\bf\Phi}{\bf A}^{-1}{\bf\Phi}^{\rm T}$として、

\begin{align}
\ln p({\bf t}|{\bf\Phi},{\bf\alpha},\beta) &= \ln\mathcal{N}({\bf t}|{\bf 0},{\bf C})\\
&= -{1\over2}\left\{N\ln(2\pi) + \ln|{\bf C}| + {\bf t}^{\rm T}{\bf C}^{-1}{\bf t}\right\}
\end{align}

となる。
これを${\bf\alpha},\beta$について微分して超パラメータの更新式が得られる。$\gamma_i=1-\alpha_i\Sigma_{ii}$として、

\begin{align}
\alpha_i^{new} &= {\gamma_i\over m_i^2}\\
\beta^{new} &= {N - \sum_i\gamma_i\over||{\bf t} - {\bf\Phi}{\bf m}||^2}
\end{align}

こうして得られた新たな超パラメータ${\bf\alpha}^{new},\beta^{new}$を用いて、再度重みパラメータ${\bf w}$の事後分布を計算してから超パラメータを更新するということを繰り返す。

関連ベクトル

今回は、特徴ベクトルに学習データ点を中心としたガウス関数を用いているので、そのパラメータ$w$の値は学習データが予測にどれだけ寄与するのかを表す値とも言えます。関連ベクトルマシンによって関連度自動決定を用いると多くのパラメータ$w$が0となり、そうでないものに対応する学習データを関連ベクトルと呼びます。予測分布を計算するときは、関連ベクトルに対応する特徴だけ用いても予測結果はあまり変わらないはずです。

実装

ライブラリ

今回もアルゴリズムの部分はnumpyだけでコードを組みます。

import matplotlib.pyplot as plt
import numpy as np

関連ベクトル回帰

# 関連ベクトル回帰を行うクラス
class RelevanceVectorRegression(object):
    # 超パラメータの初期化
    def __init__(self, alpha=1., beta=1.):
        self.alpha = alpha
        self.beta = beta

    # ガウスカーネルを用いて特徴ベクトルの計算
    def _kernel(self, x, y):
        return np.exp(-10 * (x - y) ** 2)

    # 超パラメータalpha,betaの推定
    def fit(self, x, t, iter_max=1000):
        self.x = x
        self.t = t
        N = len(x)

        # 計画行列
        Phi = self._kernel(*np.meshgrid(x, x))
        self.alphas = np.zeros(N) + self.alpha
        for _ in xrange(iter_max):
            params = np.hstack([self.alphas, self.beta])

            # 重みパラメータwの事後分布の共分散 PRML式(7.83)
            self.precision = np.diag(self.alphas) + self.beta * Phi.T.dot(Phi)
            self.covariance = np.linalg.inv(self.precision)

            # 重みパラメータwの事後分布の平均 PRML式(7.82)
            self.mean = self.beta * self.covariance.dot(Phi.T).dot(t)

            # パラメータの有効度 PRML式(7.89)
            gamma = 1 - self.alphas * np.diag(self.covariance)

            # 超パラメータの更新 PRML式(7.87)
            self.alphas = gamma / np.square(self.mean)

            # 0割りが生じないように、10^10を超えたalphaを10^10にする
            self.alphas = np.clip(self.alphas, 0, 1e10)

            # 超パラメータの更新 PRML式(7.88)
            self.beta = (N - np.sum(gamma)) / np.sum((t - Phi.dot(self.mean)) ** 2)

            # もしパラメータの更新量が小さければ終了
            if np.allclose(params, np.hstack([self.alphas, self.beta])):
                break
        else:
            # 既定の回数更新させても終了しなければ以下の文を出力
            print "paramters may not have converged"

    # 入力xに対する事後予測分布を計算
    def predict_dist(self, x):
        K = self._kernel(*np.meshgrid(x, self.x, indexing='ij'))

        # 事後予測分布の平均 PRML式(7.90)
        mean = K.dot(self.mean)

        # 事後予測分布の分散 PRML式(7.91)
        var = 1 / self.beta + np.sum(K.dot(self.covariance) * K, axis=1)

        # 事後予測分布の平均と標準偏差を返す
        return mean, np.sqrt(var)

全体のコード

relevance_vector_regression.py

import matplotlib.pyplot as plt
import numpy as np


class RelevanceVectorRegression(object):

    def __init__(self, alpha=1., beta=1.):
        self.alpha = alpha
        self.beta = beta

    def _kernel(self, x, y):
        return np.exp(-10 * (x - y) ** 2)

    def fit(self, x, t, iter_max=1000):
        self.x = x
        self.t = t
        N = len(x)
        Phi = self._kernel(*np.meshgrid(x, x))
        self.alphas = np.zeros(N) + self.alpha
        for _ in xrange(iter_max):
            params = np.hstack([self.alphas, self.beta])
            self.precision = np.diag(self.alphas) + self.beta * Phi.T.dot(Phi)
            self.covariance = np.linalg.inv(self.precision)
            self.mean = self.beta * self.covariance.dot(Phi.T).dot(t)
            gamma = 1 - self.alphas * np.diag(self.covariance)
            self.alphas = gamma / np.square(self.mean)
            self.alphas = np.clip(self.alphas, 0, 1e10)
            self.beta = (N - np.sum(gamma)) / np.sum((t - Phi.dot(self.mean)) ** 2)
            if np.allclose(params, np.hstack([self.alphas, self.beta])):
                break
        else:
            print "paramters may not have converged"

    def predict_dist(self, x):
        K = self._kernel(*np.meshgrid(x, self.x, indexing='ij'))
        mean = K.dot(self.mean)
        var = 1 / self.beta + np.sum(K.dot(self.covariance) * K, axis=1)
        return mean, np.sqrt(var)


def create_toy_data(func, low=0., high=1., n=10, std=0.1):
    x = np.random.uniform(low, high, n)
    t = func(x) + np.random.normal(scale=std, size=n)
    return x, t


def main():

    def func(x):
        return np.sin(2 * np.pi * x)

    x, t = create_toy_data(func, n=10)
    plt.scatter(x, t, color="blue", alpha=0.5, label="observation")

    regression = RelevanceVectorRegression()
    regression.fit(x, t)
    relevance_vector = np.abs(regression.mean) > 0.1

    x_test = np.linspace(0, 1, 100)
    plt.scatter(x[relevance_vector], t[relevance_vector], color="green", s=100, marker="D", label="relevance vector")
    plt.plot(x_test, func(x_test), color="blue", label="sin($2\pi x$)")
    y, y_std = regression.predict_dist(x_test)
    plt.plot(x_test, y, color="red", label="predict_mean")
    plt.fill_between(x_test, y - y_std, y + y_std, color="pink", alpha=0.5, label="predict_std")
    plt.legend()
    plt.show()


if __name__ == '__main__':
    main()

結果

青、緑点を学習データとして関連ベクトルマシンで回帰させた結果、下の図（PRML図7.9の再現）のようになりました。緑点は関連ベクトルと表しています。

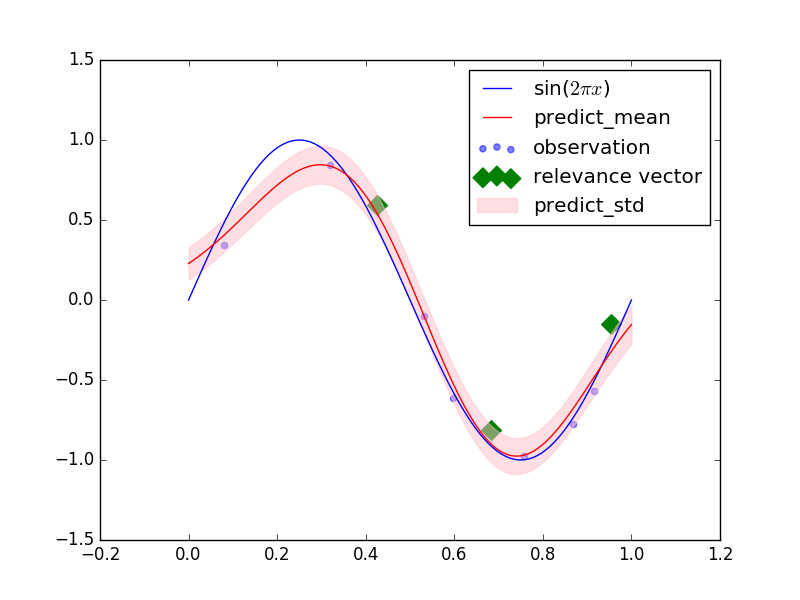
終わりに

サポートベクトルマシンと同等の汎化性能を持ちながら、より高速な予測が出来るらしいので、これを機に、サポートベクトルマシンだけでなく関連ベクトルマシンも使っていこうかと思います。出力をベイズ的に扱うことができて、分散を評価できるのも嬉しい利点です。ただ、学習データ点がないところでは予測分散が小さくなるという人間の直感に反したことになるのは残念。
今回は関連ベクトルマシンを使って回帰問題を解きましたが、もちろんロジスティックシグモイド関数を用いることで分類問題にも拡張できます。機会があればそちらも実装していきたいです。