動機
有限要素法に関する記事の多くは、ポアソン方程式を取り上げています。
二次元を扱う場合、要素分割は大抵、三角形一次要素か四角形要素であることが多く、三角形二次要素にフォーカスされたものはそれほど多くないです。
そのため、この記事では三角形二次要素を用いてポアソン方程式を解く方法を導出していこうかと思います。
今回は三角形要素に分割して局所座標系に変換するところまでやろうと思います。
次の記事→(その2)
ポアソン方程式
\nabla^2 u = f(x,y) \\
\Gamma_D : u(x,y) = u_D(x,y) ,~~~
\Gamma_N : \frac{\partial u}{\partial n} = q(x,y)
$\Gamma_D,\Gamma_N$はそれぞれディリクレ境界とノイマン境界を表しています。
なお、以下、領域は$\Omega$で表すものとします。
例えば、こんな感じです。
\begin{align}
&\Omega = \{(x,y)|0 \leq x \leq 1 , ~~~ 0 \leq y \leq 1\}\\
&\Gamma_D = \{(x,y)|0 \leq x \leq 1 , ~~~ y = 0,1 \}\\
&\Gamma_N = \{(x,y)| x=0,1 , ~~~ 0 \leq y \leq 1 \}\\
&u_D(x,y) = 0, ~~~ q(x,y) = 0
\end{align}
弱形式化
$u$の近似関数を$\hat{u}$とすると、残差$R(x,y)$は、
R(x,y) = \nabla^2 \hat{u} - f(x,y)
と表せる。
これに任意の重み関数$w(x,y)$を乗じたものを領域$\Omega$全体で積分したものが0となるような近似関数$\hat{u}$を求めてるのです。
つまり、
\int_\Omega R(x,y)w(x,y) \mathrm{d}\Omega = \int_\Omega \left[\nabla^2 \hat{u} - f(x,y)\right]w(x,y) \mathrm{d}\Omega = 0
となる、近似関数$\hat{u}$を求めたいのです。
TODO
ここで、部分積分や、ガウスの発散定理を用いると、以下のようになります。
\begin{align}
\int_\Omega \left[\nabla^2 \hat{u} - f(x,y)\right]w(x,y) \mathrm{d}\Omega
&= \int_\Omega \left[ -\nabla \hat{u}^T \nabla w(x,y) - f(x,y)w(x,y)\right] \mathrm{d}\Omega
+\int_\Gamma \left[\frac{ \partial \hat{u} }{\partial n} w(x,y) \right] \mathrm{d\Gamma}=0 \\
\end{align}
すなわち、
\int_\Omega \nabla \hat{u}^T \nabla w(x,y) \mathrm{d}\Omega +\int_\Omega f(x,y)w(x,y) \mathrm{d}\Omega =
\int_\Gamma \left[\frac{ \partial \hat{u} }{\partial n} w(x,y) \right] \mathrm{d\Gamma}
重み関数はディリクレ境界$\Gamma_D$で0となるようにとります。すると、
\begin{align}
\int_\Omega \nabla \hat{u}^T \nabla w(x,y) \mathrm{d}\Omega +\int_\Omega f(x,y)w(x,y) \mathrm{d}\Omega
&=\int_\Gamma \left[\frac{ \partial \hat{u} }{\partial n} w(x,y) \right] \mathrm{d\Gamma}\\
&=\int_{\Gamma_N} q(x,y) w(x,y) \mathrm{d\Gamma}
\end{align}
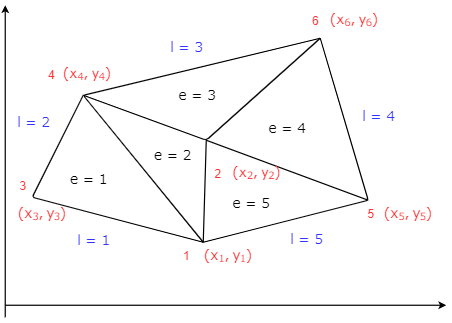
要素分割
領域で積分しているところは要素単位で、境界部分は辺単位で分割していきます。
要素が、$e=1,2,\cdots $、境界の辺が、$l = 1,2, \cdots$あるとすると、
\sum_{e=1} \left[\int_{\Omega_e} \nabla \hat{u}^T \nabla w(x,y) \mathrm{d}\Omega +\int_{\Omega_e} f(x,y)w(x,y) \mathrm{d}\Omega \right] =
\sum_{l=1} \int_{\Gamma_{N_l}} q(x,y) w(x,y) \mathrm{d\Gamma}
離散化
要素内での関数、$\hat{u}^e(x,y),f^e(x,y)$を離散化していきます。
\begin{align}
\hat{u}^e(x,y) &= u_i^e \phi_i(x,y) \\
f^e(x,y) &= f_i^e \phi_i (x,y)
\end{align}
$u_i^e,f_i^e$などは要素$e$内の$i$番目の特定の点(節点という)での値で、$\phi_i(x,y)$などは内挿関数、もしくは形状関数と言われるものです。
つまり、要素内のある物理量の分布を、節点での値と内挿関数の内積であらわしているのです。
また、境界部分(左辺)に関しては辺上で同じく形状関数$\psi_i$を導入します。
q(x,y) = q_i \psi_i(x,y)
ガラーキン法
ガラーキン法は重み関数を、求めたい物理量と同じ内挿関数の線形結合で表す方法である。
要素内では
w(x,y) = w_i^e \phi_i(x,y)
境界上では
w(x,y) = w_i^e \psi_i(x,y)
要素分割し、離散化された方程式
\begin{align}
\sum_{e=1} \left[
w_j^e u_i \mathbf{K^e}
+w_j^e \mathbf{f^e}
\right]
=
\sum_{l=1} w_j^e q_i^e \int_{\Gamma_{N_l}} \psi_i^e \psi_j^e \mathrm{d\Gamma}\\
\mathbf{K^e} = \int_{\Omega_e} \nabla \phi_i^e \nabla \phi_j^e \mathrm{d}\Omega, ~~~
\mathbf{f^e} = f_i^e \int_{\Omega_e} \phi_i^e \phi_j^e \mathrm{d}\Omega
\end{align}
以降、具体的な要素分割を考えていきます。
三角形二次要素
以下の図のような要素を考える。
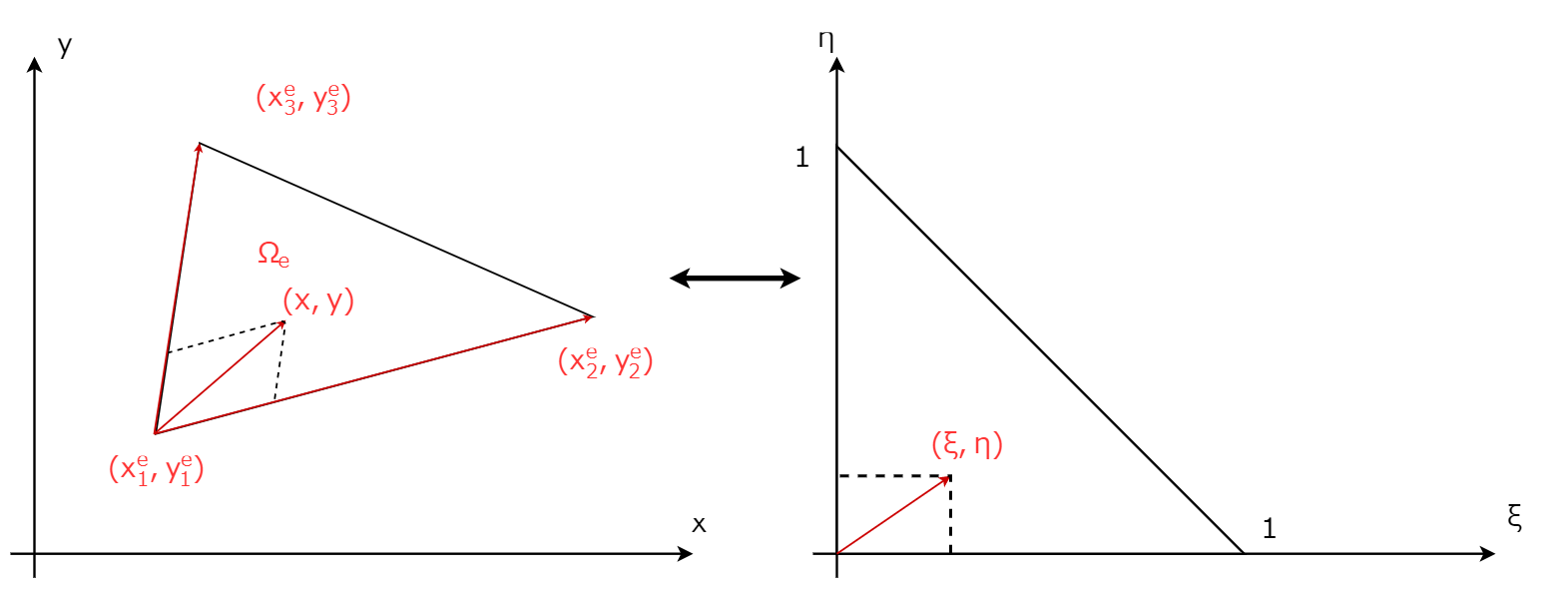
全体座標系から局所座標系へ
これから行っていく積分等の演算を楽にしていくために一つ一つの要素に変換をかけていきます。
要素内の任意の点$\mathbf{x^e}$は以下のようにして表せます。
\begin{align}
\mathbf{x^e} &= \xi (\mathbf{x_2^e}-\mathbf{x_1^e}) + \eta (\mathbf{x_3^e}-\mathbf{x_1^e}) + \mathbf{x_1^e}\\
&=
\begin{bmatrix}
\mathbf{x_2^e}-\mathbf{x_1^e}&&
\mathbf{x_3^e}-\mathbf{x_1^e}
\end{bmatrix}
\begin{bmatrix}
\xi\\
\eta
\end{bmatrix}
-\mathbf{x_1^e}
\end{align}
\begin{align}
J_e &=
\begin{pmatrix}
\frac{\partial x}{\partial \xi} & \frac{\partial x}{\partial \eta} \\
\frac{\partial y}{\partial \xi} & \frac{\partial y}{\partial \eta}
\end{pmatrix}
=\begin{pmatrix}
x_2^e - x_1^e && x_3^e - x_1^e \\
y_2^e - y_1^e&& y_3^e - y_1^e
\end{pmatrix}\\
|J_e| &=
\begin{vmatrix}
x_2^e - x_1^e && x_3^e - x_1^e \\
y_2^e - y_1^e&& y_3^e - y_1^e
\end{vmatrix}\\
&=
(x_2^e - x_1^e)(y_3^e - y_1^e) - (x_3^e - x_1^e)(y_2^e-y_1^e)
\end{align}
ヤコビアンが定数になってくれるので非常にありがたい.
しかし、めんどくさいのはここからです。
\begin{align}
\nabla &= \left(\frac{\partial}{\partial x},\frac{\partial}{\partial y} \right) \\
&=
\left( \frac{\partial \xi}{\partial x} \frac{\partial}{\partial \xi} + \frac{\partial \eta}{\partial x}\frac{\partial}{\partial \eta},
\frac{\partial \xi}{\partial y} \frac{\partial}{\partial \xi} + \frac{\partial \eta}{\partial y}\frac{\partial}{\partial \eta} \right)\\
&=
\begin{pmatrix}
\frac{\partial \xi}{\partial x} & \frac{\partial \eta}{\partial x} \\
\frac{\partial \xi}{\partial y} & \frac{\partial \eta}{\partial y}
\end{pmatrix}
\begin{pmatrix}
\frac{\partial}{\partial \xi}\\
\frac{\partial}{\partial \eta}
\end{pmatrix}
\end{align}
そして、先程は$x,y$から$\xi,\eta$を求めていましたがそれの逆を行います。
\begin{align}
\begin{pmatrix}
\xi\\
\eta
\end{pmatrix}&=
J_e^{-1}(\mathbf{x^e}-\mathbf{x_1^e})\\
\end{align}
これを用いると、ナブラを$\xi,\eta$の偏微分で表そうとしたときに出てきた行列部分をヤコビアンを用いて表せます。
\begin{align}
\begin{pmatrix}
\frac{\partial \xi}{\partial x} & \frac{\partial \eta}{\partial x} \\
\frac{\partial \xi}{\partial y} & \frac{\partial \eta}{\partial y}
\end{pmatrix}
&=
(J_e^{-1}
)^T
\end{align}
であるから、
\begin{align}
\mathbf{K^e} &= \int_{\Omega_e} \nabla \phi_i^e \nabla \phi_j^e \mathrm{d}\Omega\\
&=\int_{\Omega_e}
\left(
\begin{pmatrix}
\frac{\partial \xi}{\partial x} & \frac{\partial \eta}{\partial x} \\
\frac{\partial \xi}{\partial y} & \frac{\partial \eta}{\partial y}
\end{pmatrix}
\begin{pmatrix}
\frac{\partial \phi_i^e}{\partial \xi}\\
\frac{\partial \phi_i^e}{\partial \eta}
\end{pmatrix}
\right)^T
\left(
\begin{pmatrix}
\frac{\partial \xi}{\partial x} & \frac{\partial \eta}{\partial x} \\
\frac{\partial \xi}{\partial y} & \frac{\partial \eta}{\partial y}
\end{pmatrix}
\begin{pmatrix}
\frac{\partial \phi_j^e}{\partial \xi}\\
\frac{\partial \phi_j^e}{\partial \eta}
\end{pmatrix}
\right) |J_e|
\mathrm{d}\Omega\\
&=\int_{\Omega_e}
\begin{pmatrix}
\frac{\partial \phi_i^e}{\partial \xi} &
\frac{\partial \phi_i^e}{\partial \eta}
\end{pmatrix}
\begin{pmatrix}
\frac{\partial \xi}{\partial x} & \frac{\partial \eta}{\partial x} \\
\frac{\partial \xi}{\partial y} & \frac{\partial \eta}{\partial y}
\end{pmatrix}^T
\begin{pmatrix}
\frac{\partial \xi}{\partial x} & \frac{\partial \eta}{\partial x} \\
\frac{\partial \xi}{\partial y} & \frac{\partial \eta}{\partial y}
\end{pmatrix}
\begin{pmatrix}
\frac{\partial \phi_j^e}{\partial \xi}\\
\frac{\partial \phi_j^e}{\partial \eta}
\end{pmatrix}
|J_e|
\mathrm{d}\Omega\\
&=\int_{\Omega_e}
\begin{pmatrix}
\frac{\partial \phi_i^e}{\partial \xi} &
\frac{\partial \phi_i^e}{\partial \eta}
\end{pmatrix}
J_e^{-1} (J_e^{-1})^T
\begin{pmatrix}
\frac{\partial \phi_j^e}{\partial \xi}\\
\frac{\partial \phi_j^e}{\partial \eta}
\end{pmatrix}
|J_e|
\mathrm{d}\Omega\\
\end{align}
ここで、
J_e^{-1} (J_e^{-1})^T |J_e|=
\begin{pmatrix}
a&b\\
c&d
\end{pmatrix}
とすれば、
\begin{align}
\mathbf{K^e} &= a \int_{\Omega_e} \frac{\partial \phi_i^e}{\partial \xi} \frac{\partial \phi_j^e}{\partial \xi} \mathrm{d}\Omega
+ b \int_{\Omega_e} \frac{\partial \phi_i^e}{\partial \xi} \frac{\partial \phi_j^e}{\partial \eta} \mathrm{d}\Omega
+ c \int_{\Omega_e} \frac{\partial \phi_i^e}{\partial \eta} \frac{\partial \phi_j^e}{\partial \xi} \mathrm{d}\Omega
+ d \int_{\Omega_e} \frac{\partial \phi_i^e}{\partial \eta} \frac{\partial \phi_j^e}{\partial \eta} \mathrm{d}\Omega
\end{align}
$a,b,c,d$はヤコビアンが節点の座標から求まるのでそこから計算します。
その2では、内挿関数を求めて$\mathbf{K^e} , \mathbf{f^e}$を求めていきますが、その下準備が完了しました。
参考文献
偏微分方程式の数値解法 / 神谷紀生, 北栄輔著 東京 : 共立出版, 1998.3