軽い雰囲気でGo言語のS2 Geometry Libaryを使ってみたけど、使い方が全然分からなくて挫折。そして猛烈に反省。
というのも、ライブラリ中で多用されているCellという構造体がよく分からない。
にっちもさっちも行かなそうなので、S2 Cellsを読んで理解することにした。
主に、space-filling curve(空間充填曲線)という技術の話である。
S2 Cellsとは
S2ライブラリにおける空間の表現方法
S2では、単位球面上をcellと呼ばれる領域の集合に分解する。
各cellは4つの測地線を境界とする四角形である。
cellは階層を成している
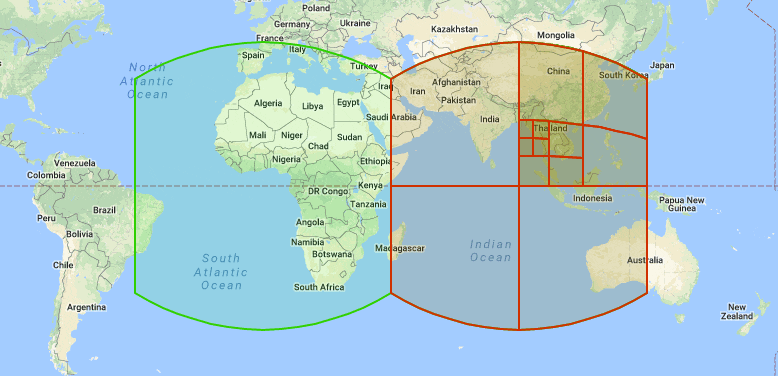
最上位の階層は、正六面体の6つの表面を単位球に被せて得られる。こんな感じか・・・
最下位の階層は、各cellを再帰的に4つの子cellに分割し得られる。
例えば、下の図には緑と赤の2つの最上位のcellがある。赤のcellは再帰的に4つの子cellに分割されていることがわかる。
各cellを構成する辺は曲線である理由は、この辺が測地線であるためである。(測地線は曲線になる。飛行機の航路と同じように。)
cellはレベルを持つ
cellが分割された回数が、そのcellのレベルとなる。レベルの範囲は0から30(計31のレベルがある。)。レベル30のcellはleaf cellと呼ばれる。故に、cellの個数の最大値は以下である。
6 \times 4^{30}
レベル30のcellは、地球上の距離に換算すると約1平方cmになる。(細か!すごい!)
各cellの換算表はこちら。
cell階層のメリット
cell階層により、空間インデックスを実装している。
そして、点集合や領域の集合は、cellによって表現(近似)される。
一般的に、点はleaf cell、領域は任意のレベルのcellとして表現される。
例えば、ハワイは以下のような22個のcellの集合で近似される。
S2CellIdとは
各cellにはユニークな識別子(64ビットの整数)が割り当てられている。これをS2CellIdと呼ぶ。
これにより、空間インデックスを用いた参照局所性が可能となる。
識別子の割り当て方
space-filling curve(空間充填曲線)順に識別子が割り当てられている。
S2では、各曲線をS2 space-filling curveと呼ぶ。
この曲線は、互いにリンクされた6つのヒルベルト曲線を含む。
これにより、球の表面を1本の連続曲線で埋め尽くすことができ、この連続曲線は全てのcellを通過する。例えば、レベル5の分割を行なった後、ヒルベルト曲線を描いた図が以下である。
レベル5のcellは曲線に従い、昇順に識別子が割り当てられる。
したがって、2つのcellが隣接していれば、それらのS2CellIdも隣接した識別子となる。これにより、局所参照性を実現している。
S2 space-filling curve曲線はヒルベルト曲線に基づいているため、より詳細に識別子の割り当て方を解説するために、ここから暫くはヒルベルト曲線についての説明が続く。
既知の方は読み飛ばしても構わない。
ヒルベルト曲線の定義
ヒルベルト曲線は、定義域(一次元の範囲)[0,1]から値域(二次元平面上の矩形)[0,1]x[0,1]を持つ関数である。この関数は、単位球上の全ての点を通る曲線となる。ヒルベルト曲線は連続であるが微分可能ではない。また、無限の長さを持つと見なす。
Hをヒルベルト曲線の定義域と値域。
H: [0,1] \rightarrow [0,1] \times [0,1]
ヒルベルト曲線の作り方
下の図のように、再帰的に正方形を分割しながら作る。
最初の分割において、正方形を4つに分割し、分割された全ての領域を通るように曲線を描く。領域を通る順番は決まっている。この例の場合、左下、左上、右上、右下、の順番で曲線が通る。
次の分割において、最初の分割で得られた領域を、さらに4つに分割し、分割された全ての領域を通るように曲線を描く。(曲線は連続するように上手いこと描かれるが、ここでは詳細は述べない。)
一次元の範囲をどのようにして二次元平面上の矩形へ写すの?
具体例で説明する。H(0.5)を二次元平面上へ写す場合を考える。
0.5を二進数表記にすると、
0.1000000000000...
となる。この2進数の小数部を2ビットで区切る。
[10,00,00,00,00,...]
区切られたものを左から順に見ていく。
最初は10で、10進数で2。次が00で、10進数で0。以下同様にして
[2,0,0,0,0,...]
が得られる。
そして、0に左下、1に左上、2に右上、3に右下と割り当てる。
すると、
[右上、左下、左下、左下、左下、...]
となる。
これに従い、以下の図のように再帰的に正方形を分割すると・・・
H(0.5) = (0.5, 0.5)
に収束する。
このようにして、一次元の範囲をどのようにして二次元平面上の矩形へ写す。
S2 space-filling curve曲線の定義
S2 space-filling curveは以下の関数である。
S: [0,6] \rightarrow S^2
この関数の定義域は一次元の範囲[0,6]、値域は単位球面上となる。
一次元の範囲をどのようにして単位球面上へ写すの?
例えば、S(1.4)を単位球面上へ写す場合を考える。
小数部を除いた整数が1。これは、正六面体の6つの表面を単位球に被せて得られる6つの面のどれであるか?を表している。
1の面は、インドが含まれている面。
そして小数部は、先ほど説明したヒルベルト曲線の0.4となる。
このようにして、一次元の範囲をどのようにして単位球面上へ写す。
識別子の割り当て方(再)
具体的なS2CellIdの割り当て方は以下である。
S2CellIdは、そのcellの中心におけるS2 curveパラメータである。(ただし、S2CellIdを整数値にするためにスケーリングされる)
具体的には例で説明する。
レベル0の面2に割り当てられる識別子は
010.1000000000...
小数部を除いた010は2(面2を表す)。
小数部0.10000000は、その面の中心を表す。
010.1000000000...は整数ではないので、スケーリングして整数にする。具体的には2の61乗をかける。得られる整数値の16進数表記は0x5000000000000000である。これがレベル0の面2に割り当てられるS2CellIdである。
ヒルベルト曲線の性質上、全てのcellの中心が重なることはないため、全てのS2CellIdは異なる数値となる。
<・・・ここから、ちょっと省略。いつか訳す>