Powered by DLHacks
見た目がなんとなく似ている物体の画像を持っていると、無性に位置の対応をとりたくなってきます。
今回は、Convolutional Neural Network (CNN) を使って画像間の位置の対応付けを行った論文を紹介します。
はじめに
下図のように、2枚の画像を入力して「意味的に」似ている部分(座標と座標の対応)を出力します。
位置の対応は、全 pixel に渡って求めるのではなく、確信度の高い点のみを出力します。
このスパースな位置の対応を Neural Best-Buddies (NBB) と呼びます。
下図では、5つの NBB を出力していることになります。
種類が違う物体であっても、それっぽい対応が取れていることが分かります。

(引用:https://github.com/kfiraberman/neural_best_buddies )
論文情報
論文:Neural Best-Buddies: Sparse Cross-Domain Correspondence [SIGGRAPH 2018]
著者:Kfir Aberman, Jing Liao, Mingyi Shi, Dani Lischinski, Baoquan Chen, Daniel Cohen-Or
実装:https://github.com/kfiraberman/neural_best_buddies (著者らの実装)
arXiv:https://arxiv.org/abs/1805.04140
引用元の表記が無い図は全て論文からの引用です。
応用先
モーフィングのような直接的な利用だけでなく、画像間の位置合わせ的なタスクが含まれる場面全般で役立ちます。
例えば、モダリティが異なる医療用画像(患者さんAのCT画像と患者さんBのMRI画像)を入力して、位置の対応が自動で得られれば、AI による診断の手がかりとして使えそうです。
手法
ざっくりとした手順は以下のようになります。
- 2枚の画像を学習済みの CNN に入力し、各層で特徴マップを得る
- 深い層から浅い層に向かって以下を繰り返す(入力層に到達する前に終わり)
- 検索対象領域内の特徴マップをマッチングして、密な対応を得る
- 特徴マップの値を使って密な対応を選別する(疎な対応を抽出する)
- 疎な対応を用いて、次の検索対象領域を決める
- 最終的な $k$ 個の対応を抽出
NBB は、2枚の画像を CNN に入力したときの特徴マップ $F$ を Coarse-to-Fine にマッチングして求めます。
CNN は pooling や stride を使って特徴量の解像度(縦横サイズ)を小さくしてくのが一般的なため、
浅い層では $F$ の解像度は大きく(Fine)、深い層では $F$ の解像度が小さくなっていきます(Coarse)。
よって、深い層で大まかな対応をとり、だんだんと浅い層に結果を伝搬させていくことで、
対応の精度を上げていくことになります。
個々の手順を掘り下げます。
1 特徴マップを得る
ImageNet で学習済みの CNN(論文中では VGG19)に2枚の画像$I_a, I_b$を入力し、特徴マップ $F_a^l, F_b^l$ を得ます。
$l$ は浅い層から深い層のものまで5種類 $(l = 5, 4, 3, 2, 1)$ を選択します。
下図(a)では、手前(深い層)から順に4つの $F$ が表示されています。
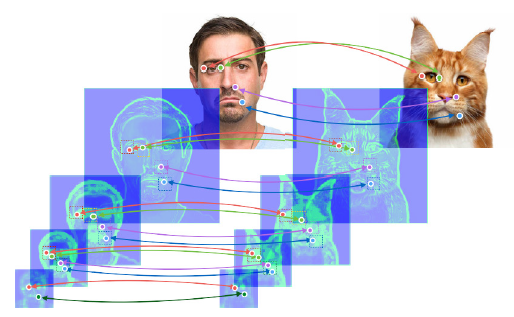
2-1 特徴マップのマッチング
深い層から順に、一つ前の繰り返しで得られた検索対象領域内で $F$ をマッチングします。
下図の緑・橙が検索対象領域で、赤・水色・青がマッチングの結果得られる対応点です。
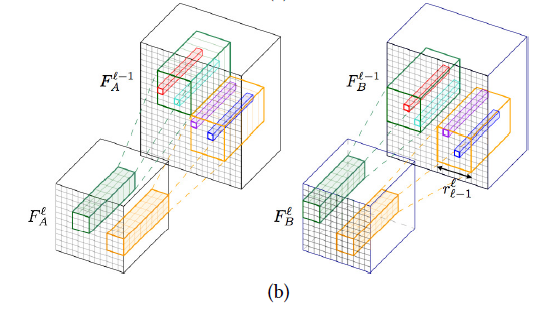
画素同士のマッチングは、着目画素を中心としたパッチの類似度が大きいものを選ぶことで得られます。
パッチの類似度は、パッチ間の相互相関(パッチ同士の内積)を用います。
この時、単純に元の $F_a, F_b$ 同士でマッチングしようとすると、うまくいかないようです。
論文では、検索対象領域同士の平均と分散を近づける instance normalization という処理を行っています。
下図で猫の画像の検索対象領域が青っぽくなっているのはこの処理の結果です。
$F_a, F_b$ の一部の領域を変換して $C_a, C_b$ を作っています。
(実際は元画像のドメインでマッチングはしないので、これはイメージだと思います。)
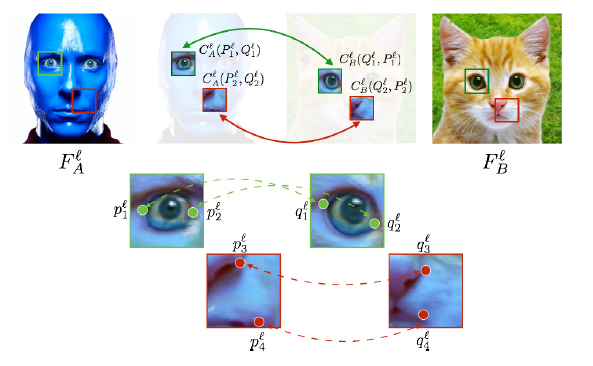
下図は、$F_a, F_b$ の検索対象領域を $C_a, C_b$ に変換しない場合(a)とする場合(b)の比較です。
変換しない場合は、色相の情報(つまりチャンネルの偏り?)によって結果が引っ張られているのが分かります。

テクい。
2-2 疎な対応を抽出
2-1 で得られた密な対応は、パッチ間の相互相関が高いものを全て選んでいるので数が膨大になります。
また、 $F$ の値が小さいところ同士でも対応が取れてしまいますが、
それらは情報量の少ない対応といえます(例:真っ白な背景同士の対応など)。
よって、2枚の画像のうち片方でも $F$ の値が小ければ、その場所の対応は情報量が少ないものとして除去します。
ちなみに $F$ は多チャンネルなので、1チャンネルにまとめる必要があります。
論文では、画素ごとにチャンネルのノルムをとって $[0-1]$ に丸めた normalized activation を用いています。
下図は normalized activation の可視化で、ライオンの体の中心部、空などの勾配が小さい部分に現れる対応は除外され、
顔や体の輪郭のような、特徴的な部分の対応のみが残ることが分かります。

閾値処理で対応点を除去することで、片方の画像だけ normalized activation が高くても、
もう片方の画像の normalized activation が低い場合は候補から削除されます。
これは、より「確信度の高い」対応を選出することに相当します。
2-3 次の検索対象領域を決定
次の検索対象領域( 2-1の図 の緑と橙)は、2-2で選別された疎な対応点を中心に直径 $r$ pixel の正方形領域とします。
$r$ は $(l = 2, 3, 4, 5)$ に対して $(r = 4, 4, 6, 6)$ のように設定しています。
ちなみに一番はじめのループでは、中心とする対応点が存在しないため、粗い特徴マップ全体を検索対象領域としています。
3 最終的なk個の対応を抽出
2-1, 2-2, 2-3 のステップが終わると、スパースな対応がいくつか得られることになります。
しかし、2-2 で normalized activation によって対応の数をいじっているため、
最終的な対応の数は入力する画像の組によって変化します。
猫とライオンの例では、以下のように特徴的な部分に対応点が集中しているのが分かります。
 |
 |
|---|
これでも良いような気がしますが、論文では点の数を減らしてさらにスパースな対応を抽出しています。
具体的には、最終的に得られた対応点を k-means でクラスタリングし、クラスタ内で代表となる点を一つ選出しています。
代表となる点は、$l (l = 1, 2, 3, 4, 5)$ を通して最も normalized activation が大きかった点(累積 normalized activation が最大となる点)としています。
$k = 10$ の時の結果は以下のようになります。
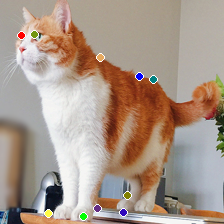 |
 |
|---|
おわりに
別ドメインの画像でもそれっぽい位置の対応を見つけてくれる Neural Best-Buddies の紹介でした。