ANNの学習の遅れについての検証

やったこと

１．関数の描画してみる
２．BP（Backpropagation）の仕組みについて再確認
３．
参考文献：ニューラルネットワークの学習の改善
　　　　：機械学習プロフェッショナルシリーズ　深層学習　著者：岡谷貴之

１．関数を描画してみる

1.1 シグモイド関数について色々と描画してみる

使用環境：pyton3.0/ Windows10/ jupyternotebook

シグモイド関数（sigmoid function）とは、以下で表される関数です。
ロジスティックシグモイド関数（logistic sigmoid function）、
または、ロジスティック関数（logistic function）とも呼ばれるようです。

y=\frac{1}{1+e^{-ax}}

この時の、a=1の場合を標準シグモイド関数と呼びます。

y=\frac{1}{1+e^{-x}}

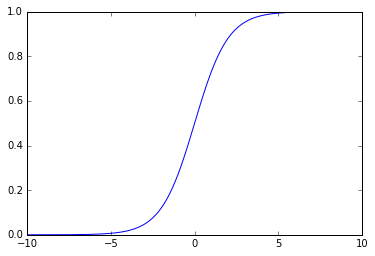
では、jupyter notebookを使ってグラフを描画してみます。

#シグモイド関数のグラフを書く

#jupyternotebokの場合%以下の文章を書かないと表示されないので注意
%matplotlib inline

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

#線形数列を作成linespace(開始値,終了値,分割数)
x=np.linspace(-10,10,1000)

#シグモイド関数に代入
y=1/(1+np.exp(-x))

#plotする
plt.plot(x,y)

#plotした関数を表示する
plt.show()

シグモイド関数の形状は以下の様になりました。

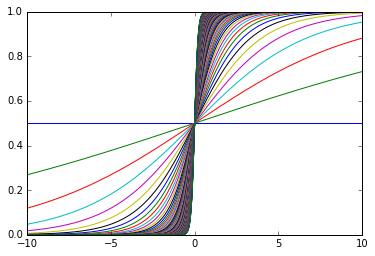
a=1の標準シグモイド関数を描画してみましたが、aの値を色々と動かしてみます。

#aの値を正の範囲で色々と動かしてみる

for a in range(0,100):
    x=np.linspace(-10,10,1000)
    y=sigmoid(0.1*a,x) 
    plt.plot(x,y)

plt.show()

値が正の時は右下から左上へ上がっていく曲線となります。
逆に負の値の時は下のグラフのように左上から右下へ下がっていきます。

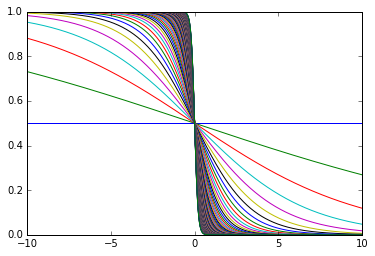
いずれにしても、シグモイド関数は0以上の値を取ることが分かります。

1.2 シグモイド関数の導関数を描画してみる

では、次にシグモイド関数の導関数を導きます。くどい様ですが、丁寧に計算していくと、以下のような式になります。

\begin{align}
y&=\frac{1}{1+e^{-ax}}\\
&=(1+e^{-ax})^{-1}\\
\end{align}

これより、xで微分すると以下のようになります。

\begin{align}
\frac{\partial y}{\partial x}&=(-1)(1+e^{-ax})^{-2} \times(-a)e^{-ax}\\
&=a\times\frac{e^{-ax}}{(1+e^{-ax})^2}\\
&=a\times\frac{1}{(1+e^{-ax})}\times\frac{e^{-ax}}{(1+e^{-ax})}\\
&=a\times\ y(1-y)
\end{align}

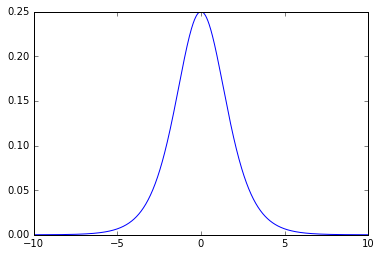
では、jupyter notebookで描画してみます。

#導関数の描画
a=1
y=sigmoid(a,x)
z=a*y*(1-y)
plt.plot(x,z)
plt.show()

このように、導関数は最大値0.25で、x=0を中心とした釣鐘型の関数となることが分かります。
例としてaの値を1から４の間で変化させてみます。

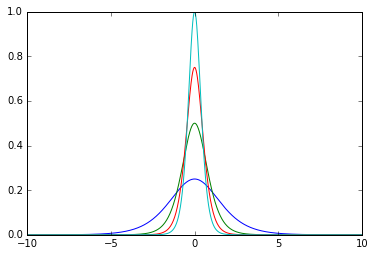
この様な形で、徐々に形状がとがって行き、最大値が増加していくのが分かります。

２．BP（Backpropagation）の仕組みについて再確認

2.1 単純なモデルケースについて

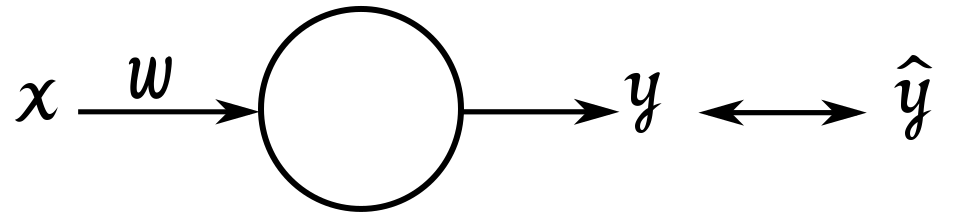
今回は、以下のような単純なユニットについて考えてみます。
参考文献と同じように、xに1が入力された時に、yに0が出力されるようなシナプスを作成します。

　　　　　　　　　　　

x:入力値　w:重み　y:出力値　\hat{y}:教師データ　閾値:b

ここで、用いるシグモイド関数は下記のような標準シグモイド関数とします。

y=\frac{1}{1+e^{-x}}

これより、x,w,yの間には以下のような式が成り立ちます。

y=\frac{1}{1+e^{-(wx+b)}}

ここで、コスト関数は次のようになります。

C=\frac{1}{2}(\hat{y}-y)^{2}

コスト関数は教師データと出力値の誤差を正の値として表現したものです。
バックプロパゲーションの計算は、このコスト関数の値（＝誤差）が最小になるように、荷重wと閾値bを学習回数毎に更新させていきます。
今回の例では入力値xは常に1ですので、定数とみることができ、yはwとbを変数とする関数と考えることができます。
したがって、今回の例では教師データyの値が0に近づくようなwとbを探すという「同定問題」としてニューラルネットワークを捉えることができます。

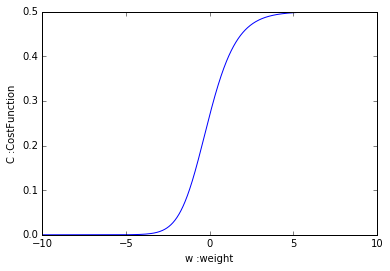
では、wを変数としたコスト関数Cの形状を調べてみましょう。仮に閾値b=1としておきます。

#重みについて-10から10までの範囲を確認
w=np.linspace(-10,10,1000)
#x=1に対してy=0を出力するような学習を行う
x=1
#閾値bはとりあえず1としてみる
b=1
y=sigmoid(1,w*x+b)
#教師データ:y_teach=0
y_teach=0
#コスト関数
c=1/2*(y_teach-y)**2
plt.plot(w,c)
plt.show()

このように、シグモイド関数と同じような形状になりました。
この状態を見ると一目瞭然ですが、Wの値は小さければ小さいほど、コスト関数Cの値は小さくなりそうです。
バックプロパゲーションでは、横軸であるWがある値のときのコスト関数Cの接線の傾きを計算し、傾きが正ならばWを負の方向へ、傾きが負ならばWを正の方向へ更新することで、コスト関数Cの値が最小値へたどり着くように計算するアルゴリズムです。

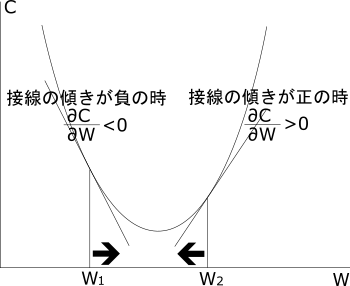
実際に偏微分を行ってみます。
wとbは独立した変数ですから、各々の変数で偏微分を行うとき、偏微分に関係ない変数は全て定数とみなすことができます。

wで偏微分してみます。

\begin{align}
\frac{\partial C}{\partial w}&=\frac{\partial C}{\partial y}\times\frac{\partial y}{\partial w}\\
&=2\times\frac{1}{2}(\hat{y}-y)\times y'\\
&=(\hat{y}-y)\times y(1-y)\\
\end{align}