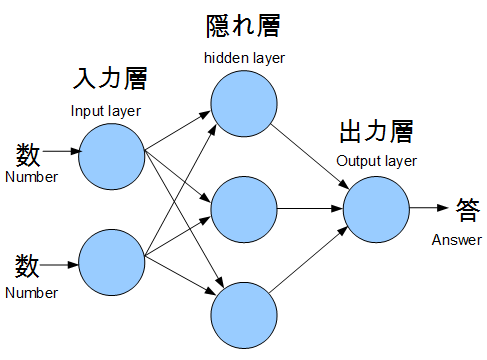
分類問題と回帰問題
1. ある事象がどのカテゴリに属するかを判定するのが分類問題。
例: 車のガソリンがあと10リットルしかないけど、砂漠で生き残れるか?
入力:ガソリン残量 10 リットル → 出力:死
入力:ガソリン残量 20 リットル → 出力:生
:
(すなわち、ガソリン残量の数値が[正、死]といういずれかのカテゴリに対応する。
こういう実例データをいっぱい集めて関係式を導き出す。)
2. ある量の入力に対してどれくらいの量が出力されるのかを推定するのが回帰問題。
例: 車のガソリンがあと10リットルしかないけど、砂漠でどのくらい走れるか?
入力:ガソリン残量 10 リットル → 出力:走行可能距離 50 km
入力:ガソリン残量 20 リットル → 出力:走行可能距離 95 km
:
ニューラルネットワーク(特に多層パーセプトロン)は前者の分類問題に使われることが多い。
ネットで拾える例題も分類問題向けが多い。
文字認識とか画像認識も分類問題と言える。
分類問題は卒業した(嘘ですけど)。
そこで回帰問題の簡単な例題を keras を使ってやってみようかと。
線形回帰と非線形回帰
A.線形回帰
上記の走行可能距離なんかは線形回帰
走行可能距離 = 燃費 × ガソリン残 ・・・(式1)
ちなみに風の影響なんかもあるかもしれない。例えば次のような関係になるならこれも線形回帰
走行可能距離 = 燃費 × ガソリン残
+ 係数 × 追い風の風速 (向かい風ならマイナス値) ・・・(式2)
一般化すると
被説明変数 = (定数項) + 係数1 × 説明変数1
+ 係数2 × 説明変数2 ・・・
・・・それぞれの説明変数の項が '+' で隔てられている。マイナスでもよい。
(だから「項」ていうんだったか)
シグマを使うとアタマよさそうに見えるか。
$$ y\,=\,C\,+\,\sum a_{i}x_{i} $$
B.非線形回帰
燃費というのは、ガソリン1リットルで走れる距離のことだが、これが道路の勾配によって変動する。
坂道を上るときは、燃費が悪くなる。出発地と目的に高低差があると、その高低差÷目的地までの距離が
平均の勾配率となって、これが燃費に影響する。たぶん。
勾配率 = 目的地までの、高低差 ÷ 距離 なんだろうけど、それはさておき、
燃費 = 定数 + 係数3 × 勾配率
(この関係式は、まあてきとうな仮説です。少なくとも係数3はマイナス値ということで)
これを(式1)に代入すると、
走行可能距離 = ( 定数 + 係数3 × 勾配率 ) × ガソリン残 ・・・(式3)
被説明変数は: 走行可能距離
説明変数は: 勾配率 と ガソリン残
こおで注目すべきなのは、式3の中で、勾配率 × ガソリン残 という、
説明変数どうしの掛け算(足し算や引き算だけでない関係)が発生してるということ。
これにより、式3は説明変数と被説明変数の非線形な関係を表すモデルといえる。
「説明変数どうしの掛け算」と言ったけど、足し算や引き算だけでなければ何でもよく、
勿論、割り算でもよく、また、説明変数がひとつだけであっても、
説明変数の2乗とか、平方根とか、指数・対数関数とか、が登場した場合も非線形な関係となる。
keras を用いて非線形回帰
ここでやっと本題にはいるけど、keras で非線形回帰モデルを扱うソースのひな形を確立しておきたい、というのが本稿の目的。
ちなみに当然、線形回帰モデルも keras で扱えるんだろうけど、線形モデルだと最小二乗法など伝統的な手法のほうが高速で精密になることが多いだろうなぁ、ということでパス。
ただ、上記の走行可能距離とかは、やや複雑で、実データを採ろうとすると、命がけで砂漠に出かけなければならない、などの理由で、極力シンプルな非線形モデルってなんだろう?
と考えて選んだのが「掛け算の九九」。
九九では、にさんがろく、すなわち、$$ 2\,*\,3\,=\,6 $$
のように、説明変数1 × 説明変数2 = 被説明変数、というな非線形モデルである。
これを回帰問題の例題として扱う。
方針としては、九九全体のうち、奇数の段(3×2とか)だけを訓練データとして学習し、
偶数の段(4×2とか)を予測対象とする。
(これで正当な評価ができるかどうかはさておき、kerasソースのひな形確立が目的なので)
ちなみに、大人の事情で、今回はマイナス値は扱わない。
ソースコード:
かいつまんでソースコードを解説。(上記コードから、一部を説明向けに変形)
keras / tensorflow をインストールしている前提。
#まず必要なライブラリをインポート。
import tensorflow as tf
import keras
from keras.optimizers import SGD
import numpy as np
from numpy.random import *
import matplotlib.pyplot as plt
import sys
import time
#学習用データを準備。
i_train, o_train = [], [] # 入力データと、正解の出力データ。
ticks = 10
max = float(ticks ** 2)
for x in range(1, ticks, 2):
for y in range(0, ticks, 1):
c = x * y / max # 九九81 なので、正解を100で割って正規化
i_train.append([x, y])
o_train.append(c)
i_train = np.array(i_train) # keras に食わせるため、numpy の配列に変換。
モデル構築
# あまり考えずにバイアス項付きとしたが、図では省略している。
# 多層パーセプトロンの中では、極めてシンプルな構造で、今流行のディープなんとかのかけらもない。
### # 入力層、隠れ層
model.add(Dense(units = 3, input_dim = 2, use_bias = true))
# 入力層は2次元で、隠れ層は1層で、隠れ層のニューロンは3個
model.add(Activation('sigmoid'))
# 隠れ層の出口の活性化関数はsigmoid。
# ここは、linear でないことが重要。なぜなら非線形モデルを扱うから。
# sigmid が最適なのかわからんが、今回は relu よりは精度が良かった。
### #出力層
model.add(Dense(units = 1, use_bias = bias))
model.add(Activation('linear'))
# 掛け算の答えを出力したいので、出力層の活性化関数は、linear(線形) にして「量」を出力。ココ重要!
#(分類問題でよく使われる softmax ではない)
sgd = SGD(lr=0.01, decay=1e-6, momentum=0.9, nesterov=True)
# sgd はテキトー。(よくわかってない)
model.compile(loss = 'mean_squared_error', optimizer = sgd)
# 損失関数は、mean_squared_error(平均二乗誤差) 。ココ重要!
# (分類問題でよく使われる sparse_categorical_crossentropy ではない)
非線形回帰モデルで用いる損失関数に関する考察(というか余談)
mean_squared_error を使って、いちおうそれらしい学習ができた。
但し、mean_squared_error は本来、線形モデルに適合した関数のような気がする。
今回のような非線形モデルには、もっと適切な損失関数を用いるべきかもしれない。
但し、最適な損失関数は、標準では用意されてないかも。
ていうか、非線形モデルでは、モデルの形ごとに損失関数が考えられるんじゃないだろうか。
たとえば、2 × 1 = 2 という正解に対して 3 という答えを出してしまう場合と
9 × 9 = 81 という正解に対して、82 という答えを出してしまう場合を比べると、
二乗誤差を計算すると、
$$ (3-2)^2\,=\,1 $$
$$ (82-81)^2\,=\,1 $$
双方とも1、という等価な誤差になる。
しかし、前者の場合は誤差率150%, 後者の場合は101% で、
前者のほうが大きな間違いだと評価すべきな気がする。
だからといって、損失関数を mean_absolute_percentage_error
とかにすると、学習が全く収束しなかったのであった。。
なので、今回はあきらめて mean_squared_error で学習した。
# 学習
model.fit(i_train, o_train, epochs = 100000, verbose = 1)
# 予測
a = []
for x in range(0, ticks, 2): # 前述のように偶数の段で予測。
for y in range(0, ticks, 1):
a.append([x, y])
p = np.array(a)
r = model.predict(p)
r_fact = r * max # 正規化した答えが出ちゃうので、正規化前のスケールに戻す。
視覚化
赤い星(奇数の段)は教師データ、青い点(偶数の段)は予測データ、
いずれも濃さは、答えの大小(正規化したもの)を表す。
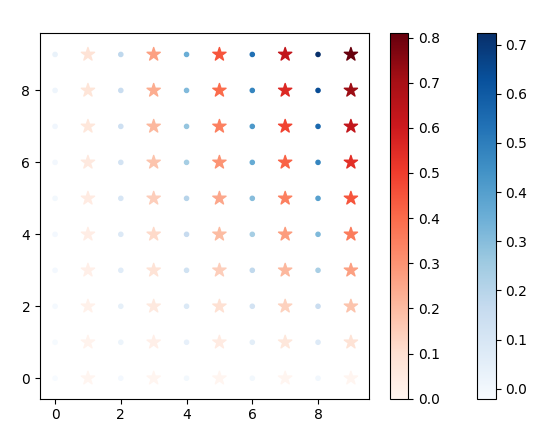
# 視覚化する意味はあまりないんだけど、楽しいから出してみただけ(^^;。視覚化ツールは上記リンク先のソース参照。
なんちゃって評価
独自のaccuracy 指標(勝手に biased_percentage と呼ぶ)で、個別の予測値を評価してみた。
100 に近いほど、より正しいと解釈されたい。
0 x 0, true_product= 0, predicted= -2.00, accuracy(biased_percentage)= 98.59 %
0 x 1, true_product= 0, predicted= -1.79, accuracy(biased_percentage)= 98.66 %
0 x 2, true_product= 0, predicted= -1.22, accuracy(biased_percentage)= 98.89 %
0 x 3, true_product= 0, predicted= -0.37, accuracy(biased_percentage)= 99.39 %
0 x 4, true_product= 0, predicted= 0.68, accuracy(biased_percentage)= 99.18 %
0 x 5, true_product= 0, predicted= 1.83, accuracy(biased_percentage)= 98.65 %
0 x 6, true_product= 0, predicted= 2.97, accuracy(biased_percentage)= 98.28 %
0 x 7, true_product= 0, predicted= 4.00, accuracy(biased_percentage)= 98.00 %
0 x 8, true_product= 0, predicted= 4.83, accuracy(biased_percentage)= 97.80 %
0 x 9, true_product= 0, predicted= 5.40, accuracy(biased_percentage)= 97.68 %
2 x 0, true_product= 0, predicted= 1.79, accuracy(biased_percentage)= 98.66 %
2 x 1, true_product= 2, predicted= 2.34, accuracy(biased_percentage)= 98.66 %
2 x 2, true_product= 4, predicted= 3.42, accuracy(biased_percentage)= 98.46 %
2 x 3, true_product= 6, predicted= 4.96, accuracy(biased_percentage)= 98.21 %
2 x 4, true_product= 8, predicted= 6.84, accuracy(biased_percentage)= 97.96 %
2 x 5, true_product= 10, predicted= 8.94, accuracy(biased_percentage)= 97.73 %
2 x 6, true_product= 12, predicted= 11.11, accuracy(biased_percentage)= 97.52 %
2 x 7, true_product= 14, predicted= 13.22, accuracy(biased_percentage)= 97.35 %
2 x 8, true_product= 16, predicted= 15.14, accuracy(biased_percentage)= 97.22 %
2 x 9, true_product= 18, predicted= 16.77, accuracy(biased_percentage)= 97.12 %
4 x 0, true_product= 0, predicted= 1.46, accuracy(biased_percentage)= 98.79 %
4 x 1, true_product= 4, predicted= 4.00, accuracy(biased_percentage)= 98.33 %
4 x 2, true_product= 8, predicted= 7.21, accuracy(biased_percentage)= 97.91 %
4 x 3, true_product= 12, predicted= 10.95, accuracy(biased_percentage)= 97.54 %
4 x 4, true_product= 16, predicted= 15.07, accuracy(biased_percentage)= 97.23 %
4 x 5, true_product= 20, predicted= 19.37, accuracy(biased_percentage)= 96.96 %
4 x 6, true_product= 24, predicted= 23.68, accuracy(biased_percentage)= 96.73 %
4 x 7, true_product= 28, predicted= 27.82, accuracy(biased_percentage)= 96.55 %
4 x 8, true_product= 32, predicted= 31.62, accuracy(biased_percentage)= 96.41 %
4 x 9, true_product= 36, predicted= 34.97, accuracy(biased_percentage)= 96.30 %
6 x 0, true_product= 0, predicted= 0.19, accuracy(biased_percentage)= 99.56 %
6 x 1, true_product= 6, predicted= 5.35, accuracy(biased_percentage)= 98.14 %
6 x 2, true_product= 12, predicted= 11.17, accuracy(biased_percentage)= 97.52 %
6 x 3, true_product= 18, predicted= 17.48, accuracy(biased_percentage)= 97.06 %
6 x 4, true_product= 24, predicted= 24.08, accuracy(biased_percentage)= 96.71 %
6 x 5, true_product= 30, predicted= 30.75, accuracy(biased_percentage)= 96.42 %
6 x 6, true_product= 36, predicted= 37.29, accuracy(biased_percentage)= 96.18 %
6 x 7, true_product= 42, predicted= 43.51, accuracy(biased_percentage)= 96.00 %
6 x 8, true_product= 48, predicted= 49.25, accuracy(biased_percentage)= 95.85 %
6 x 9, true_product= 54, predicted= 54.38, accuracy(biased_percentage)= 95.75 %
8 x 0, true_product= 0, predicted= -0.03, accuracy(biased_percentage)= 99.82 %
8 x 1, true_product= 8, predicted= 7.41, accuracy(biased_percentage)= 97.88 %
8 x 2, true_product= 16, predicted= 15.43, accuracy(biased_percentage)= 97.19 %
8 x 3, true_product= 24, predicted= 23.83, accuracy(biased_percentage)= 96.72 %
8 x 4, true_product= 32, predicted= 32.40, accuracy(biased_percentage)= 96.36 %
8 x 5, true_product= 40, predicted= 40.94, accuracy(biased_percentage)= 96.08 %
8 x 6, true_product= 48, predicted= 49.23, accuracy(biased_percentage)= 95.86 %
8 x 7, true_product= 56, predicted= 57.09, accuracy(biased_percentage)= 95.68 %
8 x 8, true_product= 64, predicted= 64.37, accuracy(biased_percentage)= 95.54 %
8 x 9, true_product= 72, predicted= 70.95, accuracy(biased_percentage)= 95.44 %
独自指標 biased_percentage =
$$ \frac{(\,\sqrt{正解値}\,-\,\sqrt{予測値の絶対値}\,+\,100 )\,*\,100}{\sqrt{正解値}\,+\,100} $$
# なんでこれを考えたかは、省略。
参考文献
こちらの文献では、掛け算を「対数の足し算」ととらえて、
対数関数 → 足し算 → 指数関数 の順で答えを求めるモデルを用いています。
アタマいいですねー。
しかしフツーの人間ってこんなややこしいこと考えずに計算してるのでは?(※)
というのが本件のモデル構築の動機でした。
参考文献> なお、パラメータの数は全部で106個です。
本件のモデルでは、パラメータ総数は15個ぐらいです。。。
どちらが正確か、という評価はしてませんが。
※注釈というか、随想。
じつは、フツーの人間の掛け算は、参考文献とも本件とも全く違ったモデルを用いていると考えられます。
参考文献や本件では、いわば「アナログ演算器」をシミュレートしています。
これくらいの量とこれくらいの量を掛け合わせれば、これくらいの量になる、という感じです。
それに対し、フツーの人間(特に日本人)は、まず九九の範囲の掛け算は「丸暗記」しています。
つまり九九データベースをもっていて、キー(例:2×3)から値(例:6)を検索してるわけですね。
九九の範囲を超える掛け算では、九九というデータベースを、筆算のようなディジタルなアルゴリズムから
参照してると考えられます。
今後は、こいつら(データベース、ディジタルなアルゴリズム、アナログ演算器)を、学習によって
ハイブリッドに自動的に組み立てるようなモデルが実用になるんじゃないかと、漠然と考える今日この頃です。
謝辞
https://qiita.com/cvusk
さん、本稿の体裁の編集、ありがとうございます!