【AtCoder解説】PythonでHHKB2020のA,B,C問題を制する！

HHKB プログラミングコンテスト 2020のA,B,C問題を、Python3でなるべく丁寧に解説していきます。

ただ解けるだけの方法ではなく、次の3つのポイントを満たす解法を解説することを目指しています。

• シンプル：余計なことを考えずに済む
• 実装が楽：ミスやバグが減ってうれしい
• 時間がかからない：パフォが上がって、後の問題に残せる時間が増える

ご質問・ご指摘はコメントかツイッターまでどうぞ
Twitter: u2dayo

目次

HHKB2020 まとめ
A問題『Keyboard』
B問題『Futon』
C問題『Neq Min』

HHKB2020 まとめ

全提出人数: 6097人

パフォーマンス

パフォ	AC	点数	時間	順位(Rated内)
200	AB----	300	34分	4904(4677)位
400	ABC---	600	114分	4141(3915)位
600	ABC---	600	53分	3476(3251)位
800	ABC---	600	31分	2773(2550)位
1000	ABC---	600	19分	2106(1885)位
1200	ABC---	600	11分	1537(1318)位
1400	ABC-E-	1100	99分	1078(873)位
1600	ABC-E-	1100	62分	740(544)位
1800	ABC-E-	1100	33分	491(314)位
2000	ABCDE-	1500	86分	309(166)位
2200	ABCDE-	1500	69分	202(80)位
2400	ABCDE-	1500	55分	142(37)位

色別の正解率

色	人数	A	B	C	D	E	F
灰	2206	98.3 %	74.9 %	37.5 %	0.3 %	0.6 %	0.0 %
茶	1254	99.5 %	97.8 %	83.0 %	2.2 %	2.5 %	0.0 %
緑	1061	99.7 %	99.2 %	96.4 %	6.1 %	20.1 %	0.0 %
水	622	99.7 %	99.7 %	99.5 %	18.0 %	60.3 %	0.0 %
青	347	99.4 %	99.4 %	99.7 %	47.5 %	89.0 %	1.1 %
黄	173	98.3 %	97.7 %	98.3 %	63.6 %	89.0 %	8.7 %
橙	41	100.0 %	100.0 %	100.0 %	87.8 %	95.1 %	58.5 %
赤	15	93.3 %	100.0 %	93.3 %	93.3 %	93.3 %	66.7 %

※表示レート、灰に初参加者は含めず

簡易解説

A問題 (6027人AC)『Keyboard』

$a, b, c$ それぞれ場合分けして解くこともできますが、大文字にするためにT.upper()を使うと楽です。

B問題 (5371人AC)『Futon』

愚直に全パターン試して数えるだけです。B問題にしては、要求される実装力がかなり高いと思います。

C問題 (4229人AC)『Neq Min』

$i$ が大きくなると制約は増える一方なので、途中で求める数字が小さくなることはありません。
$p_i$ は最大 $200000$ なので、最小値の最大は $200000 + 1$ です。
よって、使える数字が出るまで $1$ 増やし続ける方法で間に合います。

D問題 (542人AC)『Squares』[この記事では解説しません]

$(2 つの正方形の全置き方の数)-(2 つの正方形が重なる置き方の数)$ が答えです。
全置き方の数は $(N-A+1)^{2}(N-B+1)^{2}$ です。
$2$ つの正方形が重なる置き方の数は、いろいろ考えると $O(1)$ で求められます。
かなり難しいです。

E問題 (1167人AC)『Lamps』[この記事では解説しません]

「ある特定のマスが照らされるような照明の置き方は、何通りあるか？」という発想をする必要があります。全てのマスについてこれを計算して、足し合わせれば答えになります。

F問題 (54人AC)『Random Max』[この記事では解説しません]

私がわかりません。

私（うにだよ）の結果（参考）

開始5分前まで某ネトゲをやっていたとは思えない、過去最高のパフォーマンスが出ました。

A問題『Keyboard』

問題ページ：A - Keyboard

実装

「文字列 $T$ をすべて大文字にしたもの」がほしい場合は T.upper() と書きます。これを使いましょう。

コード

S = input()
T = input()

if S == "Y":
    print(T.upper())
else:
    print(T)

備考

文字列のメソッドを紹介します。どれもたまに使います。

T.upper()：すべての文字が大文字になった文字列が返ります。
T.lower()：すべての文字が小文字になった文字列が返ります。
T.capitalize()：先頭の文字が大文字に、残りが小文字になった文字列が返ります。（Japanese、Englishといった感じになります）

これらのメソッドで、T自体は変化しないことに注意してください。変化させたい場合は、このように書く必要があります。

T = T.upper()

B問題『Futon』

問題ページ：B - Futon

考察：

$H, W$ は最大 $100$ なので、布団の敷き方は縦・横に敷く場合の $2$ パターンを考慮して、おおよそ $2\times{100^{2}} = 20000$ 通り程度になります。

よって、すべての敷き方を試しても数えても間に合います。

ある敷き方を試したとき、「どちらも散らかっていないマス」ならば答えに $+1$ すればいいです。

実装

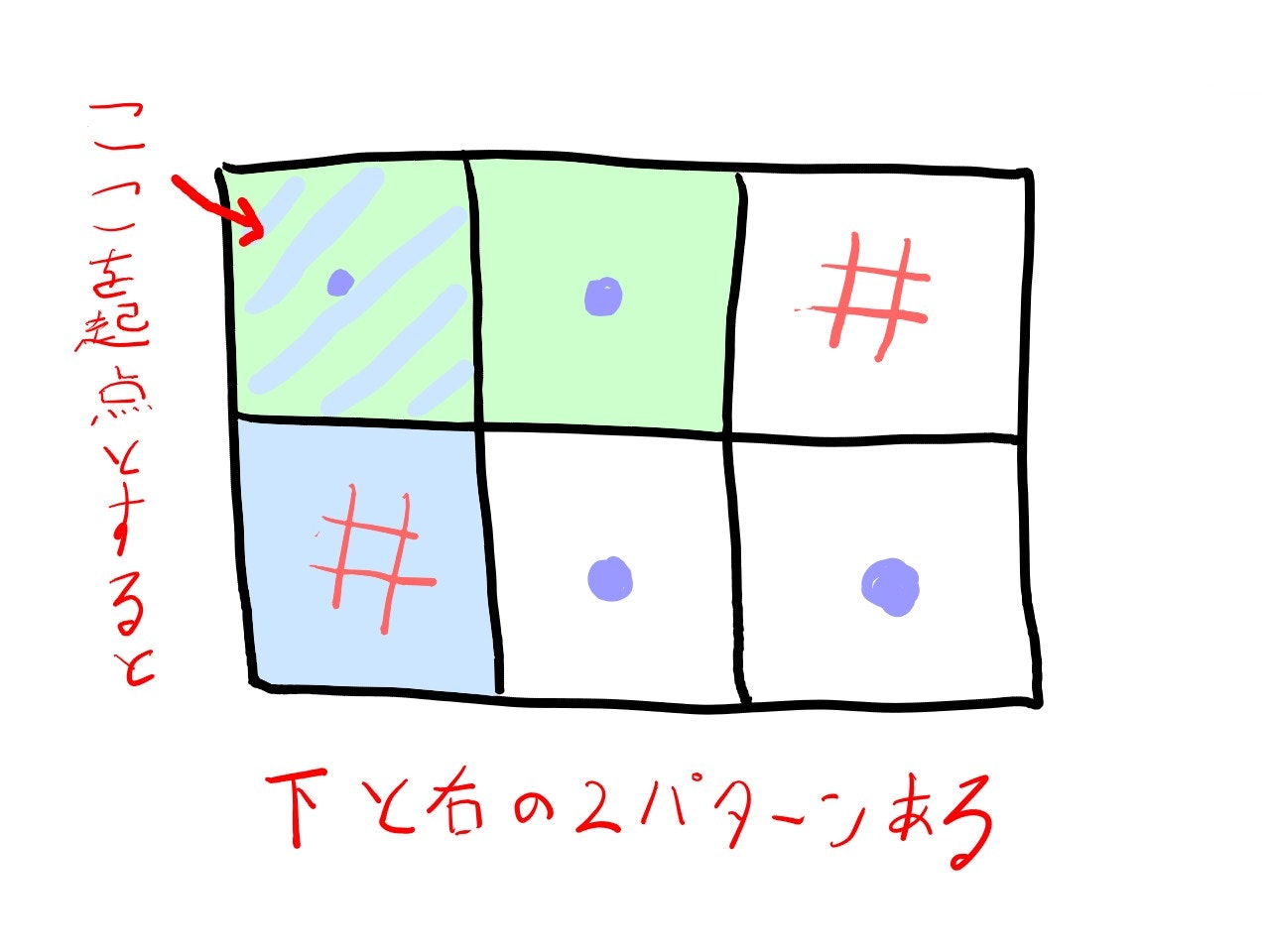
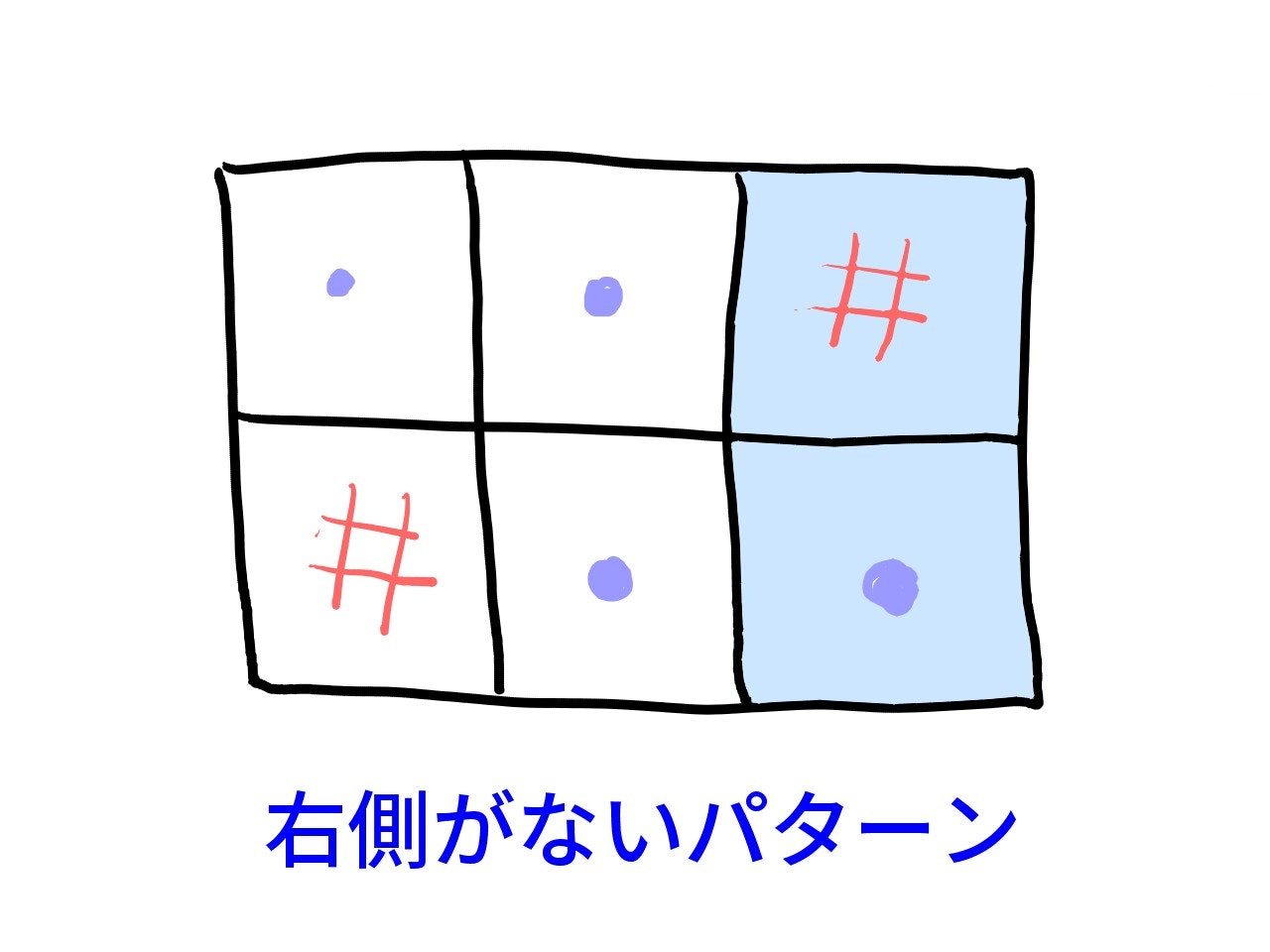
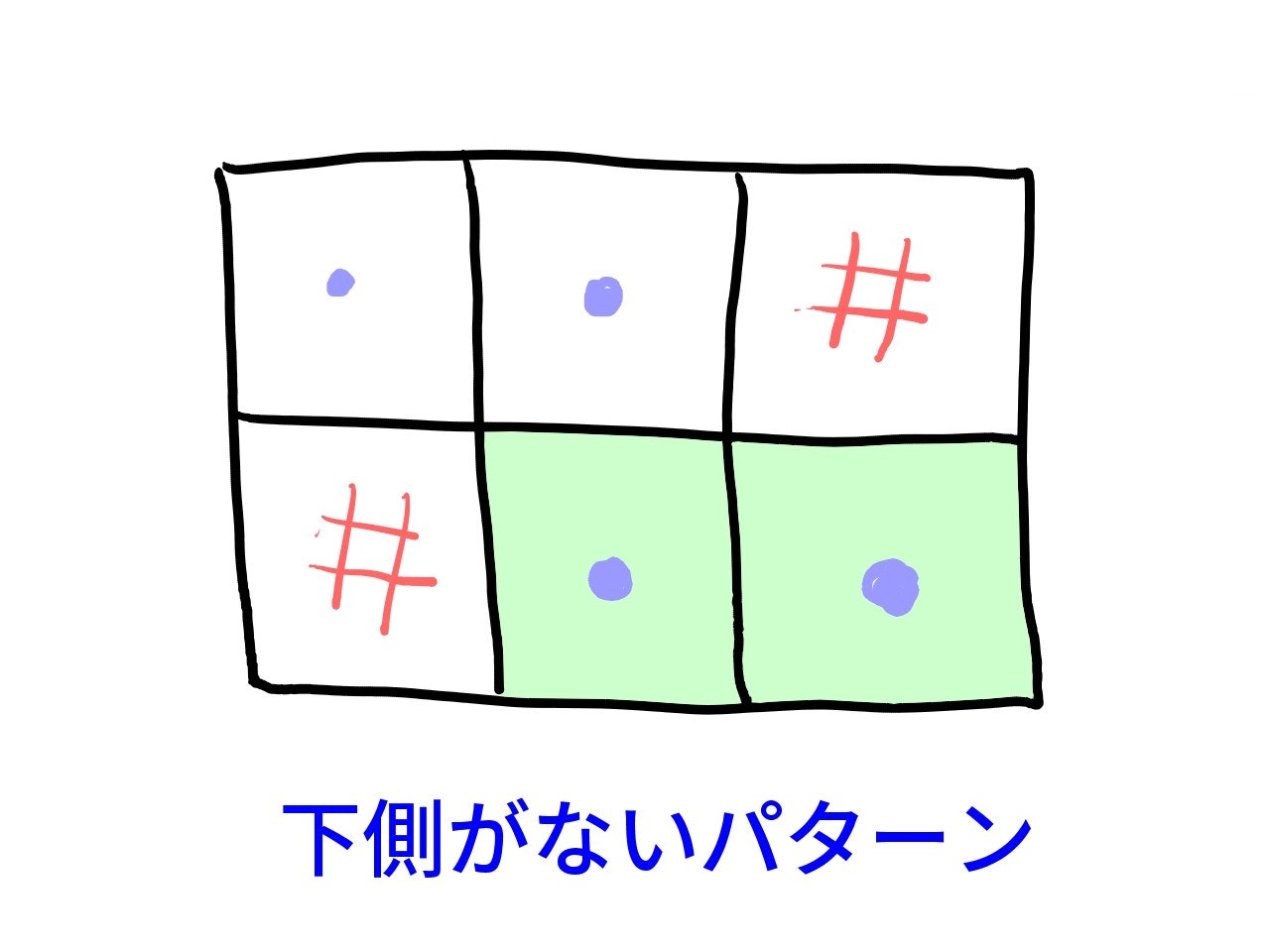
あるマスを起点に「右に向かって敷くパターン」と「下に向かって敷くパターン」の $2$ 通りを、全てのマスについて試します。これで、すべての敷き方を重複せずに試すことができます。

例えば、下の画像の場合は「下に向かって敷くパターン」は片方散らかっていて、「右に向かって敷くパターン」はどちらも散らかっていないので、$1$ 通りだけ足します。

ただし、起点が右端ならば右に敷くことはできず、下端なら下に敷くことはできません。

これに気をつけないと、配列外参照でエラーが出ます。毎回if文で確認しましょう。

コード

H, W = map(int, input().split())
grid = []  # 文字列のリストになります

for _ in range(H):
    s = input()
    grid.append(s)

ans = 0

# すべての起点を2重ループで試します
for row in range(H):
    for col in range(W):
        if grid[row][col] == ".":
            # 起点が散らかっていないことが前提です
            if col + 1 < W and grid[row][col + 1] == ".":
                # 右端ではなく、右のマスが散らかっていないなら+1
                ans += 1
            if row + 1 < H and grid[row + 1][col] == ".":
                # 下端ではなく、下のマスが散らかっていないなら+1
                ans += 1

print(ans)

C問題『Neq Min』

問題ページ：C - Neq Min

考察：

たとえば、「使える数字の候補をリストやsetで持っておいて、そこから $p_i$ を削除し、min関数で最小値を取り出す方法」は、minで最小値を得る部分に時間がかかり、およそ$O(N^2)$ になって間に合いません。

『現在の数字』の2つの特徴

$N$ 行出力する 「$0$ 以上の整数で $p_1,...,p_i$ のいずれとも等しくない値のうち最小値」 のことを、『現在の数字』 と呼ぶことにします。

何も制約がない場合、『現在の数字』 は $0$ 以上の整数で最小の $0$ です。

さて、『現在の数字』には次の $2$ つの特徴があります。

• 『現在の数字』は、$p_i$ の制約の最大値 $200000$ に $1$ 足した、 $200001$ より大きくなることはありません。
• 新たに $p_{i+1}$ が使えなくなったとき、『現在の数字』は増えるか変わらないかのどちらかで、減ることは絶対にありません。（今までの制約はそのままで、さらに制約が追加されるからです）

効率的な解き方

これらの性質を利用して、効率的にこの問題を解きます。以下、『現在の数字』の変数名をcurとします。

使われた数字を管理するリスト

$0$ ～ $200004$ までの各数字が今までの $p_i$ に出てきたかどうかを、長さ $200005$ で要素がbool（TrueかFalse）のリストusedで管理します。（used[200002]以降は使いませんが、ミスを防ぐため大きめにとっておきます）

used[k] が True なら今までの $p_i$ で $k$ が出現していて、『現在の数字』として使えないことを表します。

forループで0から順番に見ていく

初期値としてcur = 0とします。

forループで各 $i$ について、以下の操作を行います。

1. used[P[i]] をTrueにします。
2. whileループでused[cur]がTrueである間、curに $1$ 足し続けます。
3. curを出力します。

2のwhileループはcur == 200001で絶対に止まるので、計算量は大きくなりません。

以上の計算量は $O(N)$ 程度になるので、十分間に合います。

コード

N = int(input())
P = list(map(int, input().split()))

used = [False] * 200005  # 既に今までのP[i]に出現しているならTrueで、そうでなければFalseです
cur = 0  # 出力する『現在の数字』です。初期値は0以上の整数で最小の0です

for i in range(N):
    used[P[i]] = True  # P[i]が使えなくなりました（既にTrueの場合もある）
    while used[cur]:
        # 『現在の数字』として使えるものが出るまで、1足し続けます
        cur += 1
    print(cur)  # used[cur] が Falseである、最小の値が出力されます