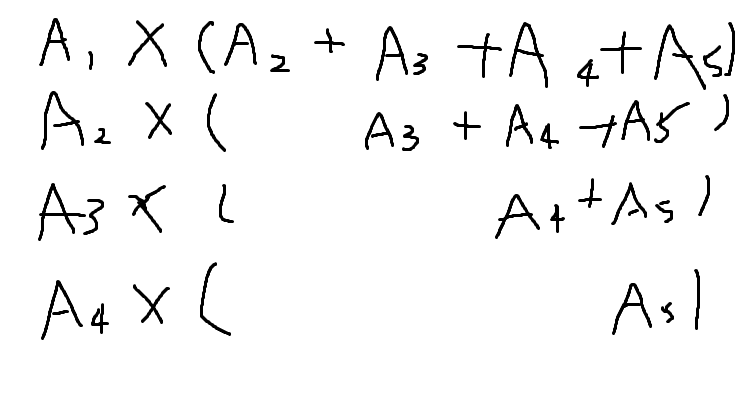【AtCoder解説】PythonでABC177のA,B,C問題を制する！

AtCoder Beginner Contest 177のA,B,C問題を、Python3でなるべく丁寧に解説していきます。

ただ解けるだけの方法ではなく、次の3つのポイントを満たす解法を解説することを目指しています。

• シンプル：余計なことを考えずに済む
• 実装が楽：ミスやバグが減ってうれしい
• 時間がかからない：パフォが上がって、後の問題に残せる時間が増える

目次

ABC177 まとめ
A問題『Don't be late』
B問題『Substring』
C問題『Sum of product of pairs』

ABC177 まとめ

全提出人数: 9630人

パフォーマンス

パフォ	AC	点数	時間	順位(Rated内)
200	AB----	300	91分	7371(7192)位
400	AB----	300	10分	6109(5930)位
600	ABC---	600	61分	5022(4847)位
800	ABCD--	1000	110分	3880(3705)位
1000	ABCD--	1000	32分	2815(2644)位
1200	ABCDE-	1500	88分	1940(1776)位
1400	ABCDE-	1500	57分	1286(1132)位
1600	ABCDE-	1500	40分	828(680)位
1800	ABCDE-	1500	30分	511(381)位
2000	ABCDE-	1500	23分	305(197)位
2200	ABCDE-	1500	16分	181(94)位
2400	ABCDEF	2100	90分	93(43)位

色別の正解率

色	人数	A	B	C	D	E	F
灰	4167	96.2 %	56.2 %	34.5 %	14.6 %	5.5 %	0.0 %
茶	1804	99.5 %	93.0 %	82.4 %	48.3 %	20.0 %	0.4 %
緑	1424	99.8 %	98.2 %	96.9 %	84.5 %	52.0 %	0.4 %
水	753	99.6 %	99.2 %	99.3 %	97.6 %	87.0 %	1.3 %
青	342	99.7 %	99.7 %	99.7 %	99.1 %	97.7 %	15.8 %
黄	148	95.3 %	93.2 %	93.9 %	94.6 %	93.2 %	31.8 %
橙	32	100.0 %	96.9 %	96.9 %	96.9 %	96.9 %	71.9 %
赤	5	100.0 %	100.0 %	100.0 %	100.0 %	100.0 %	60.0 %

※表示レート、灰に初参加者は含めず

簡易解説

A問題 (9347人AC)『Don't be late』

時間いっぱい使うと何メートル進めるか求めて、待ち合わせ場所までの距離と比べればいいです。

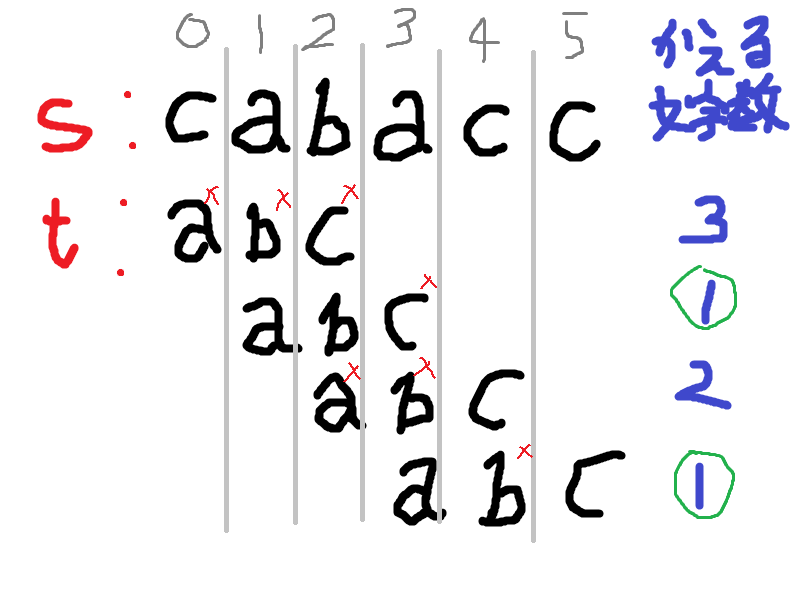
B問題 (7137人AC)『Substring』

$S$ のどの部分から $T$ と同じにするか決めると、何文字書き換えればいいかわかります。すべての始点について何文字書き換えればいいか求めて、そのうち最小のものが答えです。

C問題 (5863人AC)『Sum of product of pairs』

全ての組み合わせを試して足し合わせると、計算量が $O(N^2)$ になって間に合いません。「掛ける数が同じなら、掛けられる数を全て足し合わせてから掛けてもいい」ことを利用して、累積和の考えを使えば $O(N)$ になって間に合います。

D問題 (4125人AC)『Friends』[この記事では解説しません]

一番大きい友達の輪の人数が答えになります。これを求めるためには、UnionFindというデータ構造を使うといいです。

E問題 (2584人AC)『Coprime』[この記事では解説しません]

前半の判定は、エラトステネスの篩というアルゴリズムを利用します。後半の判定は、全要素の最大公約数をそのまま求めてしまえばいいです。

F問題 (152人AC)『I hate Shortest Path Problem』[この記事では解説しません]

始点を決めれば動き方が一意に定まるので、うまいことやるといいらしいです。

私（うにだよ）の結果（参考）

A問題『Don't be late』

問題ページ：A - Don't be late

割り算を使わずに掛け算だけで求めると、小数を扱うことによる誤差を心配せずに済みます。

実装

「何分かければ到着できるか」$( D\div{S} )$ 分 を求めてもいいのですが、結果が整数になるとは限りません。

整数ではないと何がどう不都合なのかというと、コンピュータが通常使っている仕組みでは小数を正確に表すことができないので、誤差で正しい結果がでないことがあるからです。

この問題はACになりますが、基本的にはできる限り整数だけで済ませたほうがいいです。

「時間いっぱい使うと何メートル進めるか」 $S\times{T}$ メートルを求めて、$D$ メートル以上かどうか判定すると、整数だけで計算できて安全です。

コード

D, T, S = map(int, input().split())

# 時間ぴったりはセーフなので、以上 >= を使います
if S * T >= D:
    print("Yes")
else:
    print("No")

B問題『Substring』

問題ページ：B - Substring

B問題にしてはだいぶ難しい問題です。全パターン試すことを考えましょう。

問題の意味

長さが $1000$ 文字以下の文字列 $S$ と、$S$ 以下の長さの文字列 $T$ があります。

$T$ の長さを $|T|$ とします。$S$ を好きなだけ書き換えることで、 $S$ の連続する $|T|$ 文字を取り出したとき、 $T$ と完全に一致するようにしたいです。

最低で何文字書き換える必要があるか求めてください。

考察：

※添字と合わせるために、0文字目から数えることにします

ひとまず、どうすれば最小文字数になるかは気にしないことにします。

例えば、「$S$ の $0$ 文字目から、連続する $|T|$ 文字」を、 $T$ と一致させようとしたとき、何文字書き換えればいいか、どう求めればいいでしょうか。

これは単に、「$S$ の $0$ 文字目から、連続する $|T|$ 文字」と、$T$ が何文字違うか数えればいいです。

「$S$ の $1$ 文字目から 連続する $|T|$ 文字」を、 $T$ と一致させようと思ったときも同じです。

この要領で全パターン試してみて、一番文字数が少ないものを答えればいいです。計算量は $O(|S||T|)$ です。

コード

S = input()
T = input()

ans = 1000000  # 適当に1001以上を初期値にしておきます

# Tが1文字のときlen(S)回、2文字のときlen(S) - 1回 …… なので、
# len(S) - len(T) + 1 回です
for i in range(len(S) - len(T) + 1):
    score = 0
    U = S[i:i + len(T)]  # Sのi文字目から連続するlen(T)文字を、Uとします
    for j in range(len(T)):
        if U[j] != T[j]:
            score += 1
    ans = min(ans, score)

print(ans)

C問題『Sum of product of pairs』

問題ページ：C - Sum of product of pairs

これもC問題としては難しいほうだと思います。『累積和』的な発想が鍵です。

考察：

全組み合わせを掛け算して、足し合わせるだけで解ければ簡単なのですが、計算量が $O(N^2)$ になって間に合いません。組み合わせ数は $\frac{N(N-1)}{2}$ 組あるので、$N=2\times{10^5}$ のとき、およそ $2\times{10^{10}} = 200$ 億組もあります。

ですので、もっと効率的に求める必要があります。

まとめて計算したい

$N = 5$で説明します。掛け算する組は、全部で $4 + 3 + 2 + 1 = 10$ 組あります。

先にくるほうの数 $A_i$ ごとに並べてみると、$A_i$ が同じ組み合わせを、下のようにまとめられることに気づけるかもしれません。

$A_1\times{(A_2 + A_3 + A_4 + A_5)}$

$A_2\times{(A_3 + A_4 + A_5)}$

$A_3\times{(A_4 + A_5)}$

$A_4\times{(A_5)}$

カッコ内を高速に求められれば、$O(N)$ で答えを出すことができて、間に合いそうです。

カッコ内の規則性

カッコ内の規則性に着目しましょう。順番に、$A_2, A_3, A_4$と1個ずつなくなっていっています。

先に $A$ すべての合計を求めておいて、掛け算するたびに、合計から使わない数$1$つ引けば、カッコ内を簡単に求めることができます。

実装

はじめに、$A_1$ ～ $A_N$ までの全ての合計 $S$ をsum(A)で求めます。

$A_1$ の掛け算を求めるとき、$S$ から $A_1$ を引きます。そして、$A_1\times{S}$ を $ans$ に足します。

$A_2$ の掛け算を求めるとき、$S$ から $A_2$ を引きます。$A_1$ はすでに引いてあります。そして、$A_2\times{S}$ を $ans$ に足します。

これを $A_N$ まで繰り返せばいいです。

余りについて

余りを取った結果を求めろと書いてあります。 C問題で余りを取らせるのは珍しいですが、D問題以降だとよく出てきます。

なぜ余りを求めさせるのかというと、「答えがとてつもなく巨大な数になってまともに計算できなくなる場合でも、余りを取ってしまえば計算できるようになる」からです。

Pythonはオーバーフローしませんが、他の言語では通常、巨大な数を扱うとオーバーフローしてしまいます。

さて、ここで重要なことがあります。「足し算、引き算、掛け算の場合、余りを取ってから計算してもいい」です。　

いちいち余りを取ることで、計算途中で巨大な数になってTLEにならずに済みます。

コード

MOD = 10 ** 9 + 7  # MODは変数に入れてしまったほうが打ち間違えなくていいです

N = int(input())
A = list(map(int, input().split()))

S = sum(A) % MOD
ans = 0

# A_Nも含まれてしまいますが、そのときはs=0なので問題ありません
for x in A:
    S -= x  # 自分と自分自身を掛けないように、先に引く必要があります
    S %= MOD  # MODはいちいち取っておくといいです
    ans += S * x
    ans %= MOD

ans %= MOD  # この行は完全に不要ですが、最後だけMODを取り忘れてWAになるミスは非常によくあるので、必要以上に取っておくと安心できます
print(ans)

余談

10億7ってなんだ

$10^9 + 7$ （$10$ 億 $7$）は素数です。余りを取るときに素数だといろいろと都合がいいので、$10$ 億に近いキリのいい数字が選ばれています。AtCoderをいっぱいやっている人にとっては、親の顔より見た素数です。

余りの世界の割り算について

余りの世界では「足し算、引き算、掛け算の場合、余りを取ってから計算してもいい」のですが、割り算は話が違います。

『逆元』というものを求めて、それを掛ける必要があります。逆元を求めること自体は簡単なのですが、話はやや難しいので、興味のある方は調べてみてください。　

逆元の求め方

具体的には、逆元はpow(x, MOD-2, MOD)で求められます。「$x$ の $MOD-2$ 乗を $MOD$ で割った余り」です。

「$10$ 億 $5$ 乗もしたら一生計算が終わらないんじゃ」という気がしますが、累乗は『繰り返し二乗法』というアルゴリズムを使うと $O(logN)$ で計算することができます。Pythonは内部でこれを使っているので、一瞬で求められます。

また、Python 3.8以上では pow(x, -1, MOD) でも求められます。PyPyではまだ使えないので気をつけてください。