AtCoder Beginner Contest 198のA,B,C問題を、Python3でなるべく丁寧に解説していきます。
ただ解けるだけの方法ではなく、次の3つのポイントを満たす解法を解説することを目指しています。
- シンプル:余計なことを考えずに済む
- 実装が楽:ミスやバグが減ってうれしい
- 時間がかからない:パフォが上がって、後の問題に残せる時間が増える
ご質問・ご指摘はコメントかツイッターまでどうぞ!
Twitter: u2dayo
よかったらLGTMしていただけると、私のやる気がでます!
目次
ABC198 まとめ
A問題『Div』
B問題『Palindrome with leading zeros』
C問題『Compass Walking』
個人的なおしらせ
ニートをやめて働き始めたので、もしかすると解説を書く時間を取りづらくなるかもしれません。やめるつもりはありませんが、睡眠時間を確保したいので、翌日や翌々日に書くことが増えるかもしれません。
また、D問題やE問題が簡単だった場合、需要がかなりありそうだと感じたため、余裕があればそちらの解説も書きたいと考えています。これは間違いなく当日中に書き終えられないので、後日書くことにします。(まだあんまり考えていませんが、たぶん別記事で書くと思います)
アプリ AtCoderFacts を開発しています
コンテストの統計データを見られるアプリ『AtCoderFacts』を作りました。
現在のところ、次の3つのデータを見ることができます。
- レート別問題正解率
- パフォーマンス目安
- 早解きで上昇するパフォーマンス
今後も機能を追加していく予定です。使ってくれると喜びます。
ABC198 まとめ
全提出人数: 8172人
パフォーマンス
| パフォ | AC | 点数 | 時間 | 順位(Rated内) |
|---|---|---|---|---|
| 200 | AB---- | 300 | 49分 | 6167(5968)位 |
| 400 | AB---- | 300 | 13分 | 5079(4880)位 |
| 600 | ABC--- | 600 | 97分 | 4156(3964)位 |
| 800 | ABC--- | 600 | 55分 | 3197(3005)位 |
| 1000 | ABC--- | 600 | 28分 | 2318(2126)位 |
| 1200 | ABCD-- | 1000 | 72分 | 1612(1424)位 |
| 1400 | ABC-E- | 1100 | 43分 | 1095(912)位 |
| 1600 | ABCDE- | 1500 | 95分 | 716(553)位 |
| 1800 | ABCDE- | 1500 | 73分 | 460(313)位 |
| 2000 | ABCDE- | 1500 | 58分 | 283(162)位 |
| 2200 | ABCDE- | 1500 | 47分 | 166(77)位 |
| 2400 | ABCDE- | 1500 | 39分 | 106(34)位 |
色別の正解率
| 色 | 人数 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|---|
| 灰 | 3378 | 96.5 % | 76.3 % | 35.0 % | 2.0 % | 2.8 % | 0.0 % |
| 茶 | 1429 | 99.4 % | 97.9 % | 67.1 % | 10.7 % | 11.3 % | 0.0 % |
| 緑 | 1090 | 99.5 % | 99.0 % | 79.1 % | 30.2 % | 35.2 % | 0.0 % |
| 水 | 623 | 99.7 % | 99.5 % | 87.6 % | 65.2 % | 72.9 % | 0.2 % |
| 青 | 351 | 100.0 % | 99.7 % | 95.7 % | 90.0 % | 94.6 % | 0.3 % |
| 黄 | 158 | 95.6 % | 94.3 % | 90.5 % | 91.1 % | 94.3 % | 6.3 % |
| 橙 | 33 | 97.0 % | 97.0 % | 93.9 % | 97.0 % | 97.0 % | 42.4 % |
| 赤 | 11 | 100.0 % | 100.0 % | 100.0 % | 100.0 % | 100.0 % | 81.8 % |
※表示レート、灰に初参加者は含めず
私(うにだよ)の結果
AGCで黄パフォとった分がほとんど吹っ飛んで泣いています。
Cは法則は一瞬でわかりましたが、どう実装するかで無限に悩んでしまいました。Eは瞬殺できましたが、焦ったせいでDでおかしなDFS方針を選んでしまって解けず、散々な結果に終わりました……。
A問題『Div』
問題ページ:A - Div
灰コーダー正解率:96.5 %
茶コーダー正解率:99.4 %
緑コーダー正解率:99.5 %
考察
A君のもらうお菓子の数 $X$ を決めると、B君がもらうお菓子の数は残り $N - X$ 個 になります。
A君が $1$ 個以上のお菓子もらう方法は、$1$ ~ $N$ 個の $N$ 通りあります。
ただし、A君が $N$ 個全部もらってしまうと、B君のお菓子が $0$ 個になってしまうのでダメです。
よって、A君が $1$ ~ $N-1$ 個のお菓子をもらう分け方 $N-1$ 通りが条件を満たすので、答えは $N-1$ です。
コード
N = int(input())
print(N - 1)
B問題『Palindrome with leading zeros』
問題ページ:B - Palindrome with leading zeros
灰コーダー正解率:76.3 %
茶コーダー正解率:97.9 %
緑コーダー正解率:99.0 %
考察
頭に"0"を何個つけるか全探索して、回文になるものを探します。
実装
まず、入力は文字列 $S$ として受け取ってください。このほうが、後々楽です。
頭に"0"をいくつかつけた文字列の作り方
forループを用いて、このように書きます。
『先頭に $0$ 個以上の $0$ をつける』とありますから、$0$ 個つける(空文字列をつける)場合も判定するように注意してください。
for i in range(100):
Z = "0" * i # i == 0なら、空文字列になります i == 3なら "000" です
T = Z + S # S の頭に、Zをくっつけます
回文判定
回文とは「ひっくり返しても自分自身と同じになる文字列」のことです。当たり前ですね。
つまり、文字列Tが回文か判定するには『文字列T』と『文字列Tを反転したもの』が同じであるかどうか見ればいいです。
スライスを用いて書くと、こうなります。非常に簡潔です。
if T == T[::-1]:
# 回文だったときの処理
コード
S = input()
def judge():
# Sは最大10桁ですから、頭につける0の数は9個まで試せば十分です。
# ただ、そういう事を考えるのが面倒なので適当に100個程度まで試します
for i in range(100):
Z = "0" * i
T = Z + S
if T == T[::-1]:
# 回文なのでTrueを返します
return True
# どうやっても回文にならないので、Falseです
return False
if judge():
print("Yes")
else:
print("No")
C問題『Compass Walking』
問題ページ:C - Compass Walking
灰コーダー正解率:35.0 %
茶コーダー正解率:67.1 %
緑コーダー正解率:79.1 %
考察
問題文に到達不能である場合の出力指示がありません。実際、どのような場合でも必ず到達することが可能です。
1回移動する場合
$1$ 回 移動すると、距離が $R$ である座標であればどこにでもいけます。これは当然ですね。
2回移動する場合
$2$ 回 移動すると、${0}\le{d}\le{2R}$ であるような距離 $d$ の座標であれば、どこにでも移動することができます。
$d = 0$ は行って戻ってくるだけなので、やる必要はありません。
$d = R$ は $1$ 回移動するだけでもできるので、$2$回かけて移動するのは無駄です。
$d = 2R$ は、全く同じ方向に $2$ 回進めば良いです。
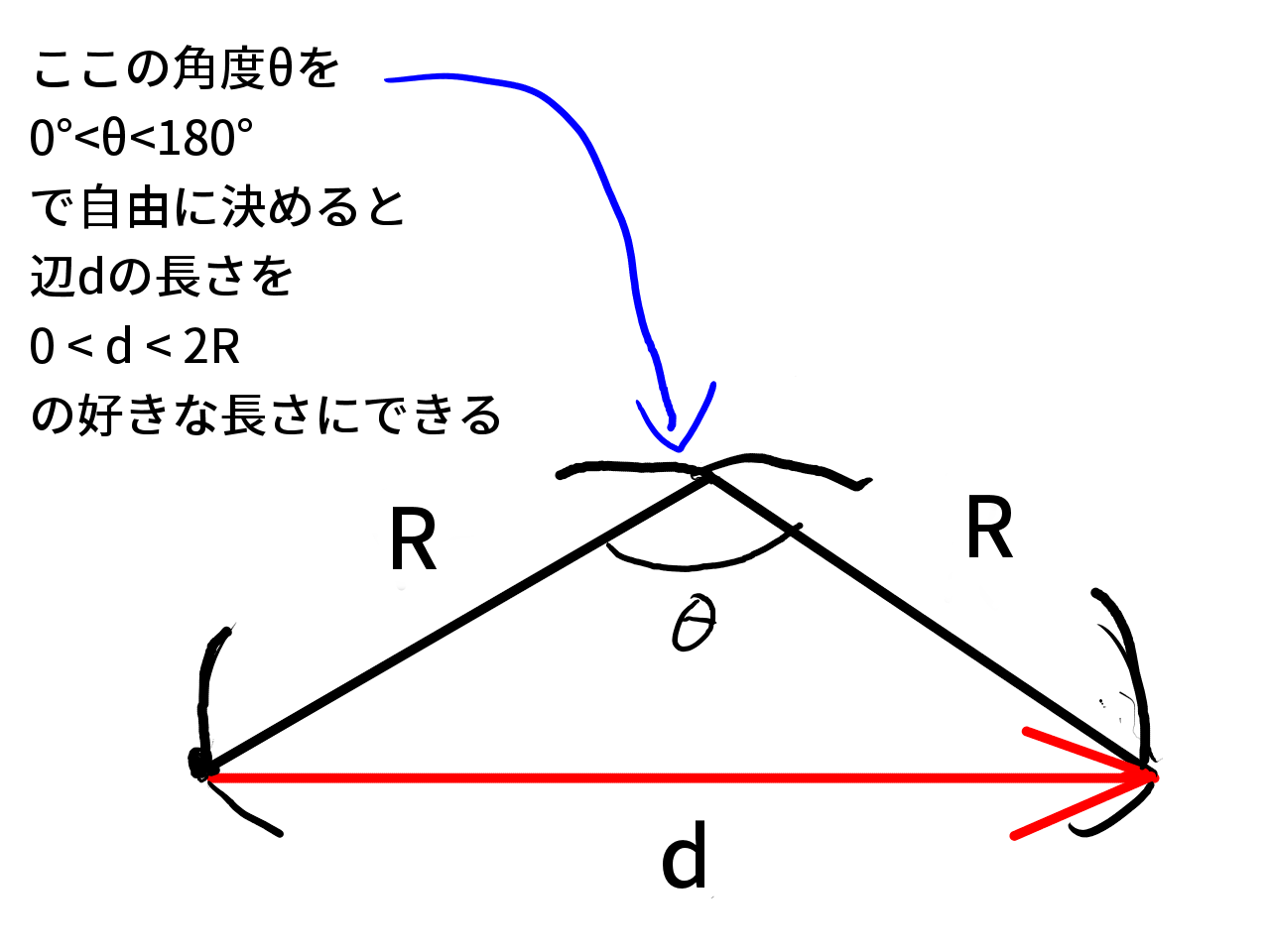
それ以外の場合を考えます。二等辺三角形を思い浮かべてみてください。
この二等辺三角形を適当に回転させれば、どんな向きにでも進めます。
最適な移動方法
$1$ 回移動するパターン、$2$ 回移動するパターンのどちらでも、好きな向きに進むことができます。ですので、できる限りゴールの$(X,\ Y) $に向かって一直線に進むのが最適です。
つまり、原点から $(X,\ Y)$ までの距離 $D = \sqrt{X^2 + Y^2}$ だけが重要で、座標自体はどうでもいいです。
距離
原点から点 $(X,\ Y)$ までの距離を $D = \sqrt{X^2 + Y^2}$ とします。
また、$D÷R$ の商を$A$、余りを$B$とします。
パターン1: B = 0 の場合
もし余り $B=0$、つまり $D$ が $R$ で割り切れるなら、$A$ が 答えです。
最短距離で真っ直ぐ $A$ 回進むだけです。
パターン2: B > 0 の場合
$B\gt{0}$、$D$ が $R$ で割り切れない場合を考えます。
まず、最短距離で真っ直ぐ $A-1$ 回進みます。すると、残りの距離は $R + B$ です。$B$ は 『$D$ を $R$ で割った余り』なので、$B < R$ です。ということは、$R < R + B < 2R$ です。
先程書いた通り、$0 < d < 2R$ である座標は $2$ 回の移動で到達することができます。
よって、答えは $(A - 1) + 2 = A + 1$ 回です。
パターン1, 2をまとめてみる
パターン1とパターン2は $\lceil\frac{D}{R}\rceil$ 回 とまとめて書くことができます。$\frac{D}{R}$の小数点以下を切り上げた値という意味です。
コーナーケース: D < Rの場合
ただし、この問題にはコーナーケースがあります。距離 $D$ が、移動できる距離 $R$ より小さい場合です。
$\lceil\frac{D}{R}\rceil = 1$ になりますが、実際は $1$ 回の移動ではゴールを通り越してしまうので、到達できません。
距離が $0 < d < 2R$ の座標には $2$ 回で到達できますから、答えは $2$ 回です。
実装
浮動小数点数を扱うと誤差が出る恐れがありますが、今回の問題では制約が小さいために使ってもACできるので、素直に使うことにします。
コード
import math
R, X, Y = map(int, input().split())
D = math.sqrt(X ** 2 + Y ** 2) # (X ** 2 + Y ** 2) ** 0.5 でもいいです
if D < R:
print(2)
else:
print(math.ceil(D / R))