概要

前回の記事では，可制御性が満たされるシステムで，状態フィードバックによって極を自由に配置することができました．
【制御工学】極配置(レギュレータの設計)を行うプログラムをつくってみた！
状態フィードバックでは，全ての内部状態をフィードバックしていました．
しかし，高次元のシステムでは全ての状態をセンサによって直接観測することは難しそうです．
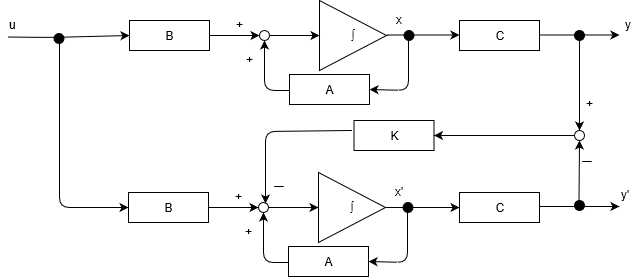
そこで登場するのが，システムの入力と出力だけから内部状態を推定する機能を持つオブザーバです．
今回は，オブザーバゲインの設計を自動で計算してくれるプログラムを作っていこうと思います．

MATLABやScilab，PythonControlを使えば，簡単にできますが，
今回もあえて，行列操作の練習の意味合いも込めて，プログラムをつくってみました．

動作環境

Windows10(64bit)
Python 3.7.2

オブザーバ

今回も証明等は置いといて，結果だけを使っていきたいと思います．

システムが可観測であれば，以下のようなオブザーバを設計することができました．


\begin{cases}
\dot{x} & = A\hat{x}-K(y-\hat{y})+Bu\\
& = (A+KC)\hat{x}-KY+Bu\\
\hat{y} & = C\hat{x}
\end{cases}

特に，システムが1出力であれば，極が任意に与えられた多項式
$p(s) = s^n + \beta_{n-1}s^{n-1} + \cdots + \beta_{1}s + \beta_0$
の根に一致するオブザーバゲインは次式で与えられました．
ただし，$\alpha_0, \alpha_1, \cdots, \alpha_{n-1}$は$A$の特性多項式
$det(sI-A) = s^n + \alpha_{n-1}s^{n-1} + \cdots + \alpha_{1}s + \alpha_0$
の係数であり，$T=(U_{c}V)^{-1}$です．


k = T^{-1}\begin{bmatrix}
\alpha_0-\beta_0\\
\vdots
\alpha_{n-1}\beta_{n-1}\\
\end{bmatrix}

コード

では，早速実装していきましょう．

estim.py


"""オブザーバゲインを求めるプログラム"""
import numpy as np

# オブザーバの極
# ---------------------------------------------------------
new_pole = [-2, -2, -2]
# ---------------------------------------------------------

# 状態空間表現
# ---------------------------------------------------------
A = np.array([[0,1,0],[1,1,-1],[0,0,1]])
c = np.array([0,1,0])

dim = np.shape(A)[0]
print("A = \n"+ str(A) + "\n")
print("c = \n"+ str(c) + "\n")
# ---------------------------------------------------------

# 固有多項式の係数を求める
# ---------------------------------------------------------
eig = np.linalg.eigvals(A)
sI_A = np.poly1d(eig, True, variable='s')
# print('sI_A = \n' + str(sI_A) + "\n")

print(np.array(sI_A))
alpha = np.round(sI_A)
alpha = alpha[::-1]
# print('alpha = \n' + str(alpha) + "\n")
# ---------------------------------------------------------

# 可観測行列
# ---------------------------------------------------------
Uo = np.array(c)
for i in range(dim - 1):
    if i == 0:
        temp =c
    else:
        temp = Uo[i,:]
    # print('temp =' +str(temp) + "\n")
    # print('Uc =' +str(Uo) + "\n")
    Uo = np.vstack((Uo, np.dot(temp, A)))

print("Uo = \n"+ str(Uo) + "\n")

rank_Uo = np.linalg.matrix_rank(Uo)
print("rank_U0 = " + str(rank_Uo) + "\n")
# ---------------------------------------------------------

# 行列Vを求める
# ---------------------------------------------------------
V = np.zeros((dim, dim))
for y in range(dim):
    for x in range(dim):
        if x + y < dim - 1:
            V[y,x] = alpha[x+y+1]
        elif x + y == dim - 1:
            V[y,x] = 1

print("V = \n"+ str(V) + "\n")
# ---------------------------------------------------------


# 変換行列Tを求める
# ---------------------------------------------------------
To = np.dot(V, Uo)
print("To = VUo = \n"+ str(To) + "\n")
To_inv = np.linalg.inv(To)
print("To^-1 = (VUo) = \n"+ str(To_inv) + "\n")
# ---------------------------------------------------------

# オブザーバゲインを求める
# ---------------------------------------------------------
p_s = np.poly1d(new_pole, True, variable='s')
# print('p_s = \n' + str(p_s) + "\n")

beta = np.round(np.array(p_s))
beta = beta[::-1]
# print('beta = \n' + str(beta) + "\n")

a_b = alpha-beta
a_b = np.delete(a_b, dim, 0)
a_b = np.reshape(a_b, (dim, 1))
# print('a_b = \n' + str(a_b) + "\n")

k = np.dot(To_inv, a_b)
print("k = \n"+ str(k) + "\n")
# ---------------------------------------------------------

解説

では，解説をしていきます．

オブザーバの極の指定


new_pole = [-2, -2, -2]

まずはじめに，オブザーバの極を指定します．
これは，つまりA+kcの固有値ですね．

状態空間の登録


A = np.array([[0,1,0],[1,1,-1],[0,0,1]])
c = np.array([0,1,0])

dim = np.shape(A)[0]

次に，状態空間を登録し，システムの次元数を取得しておきます．
いまは，以下のようなシステムにします．また，ベクトルbは使わないので登録していません．


A = \begin{bmatrix}
0 & 1 & 0\\
1 & 1 & -1\\
0 & 0 & 1
\end{bmatrix}\\

c = \begin{bmatrix}
0 & 1 & 0
\end{bmatrix}

システムの次元数の取得は，np.shape()で行いました．
np.shape()は行列の形を$n$行$m$列を$(n,m)$というタプルで返すため，
その0番目のみを取得します．今回は正方行列なので1番目でも構いません．

固有多項式の係数を求める


eig = np.linalg.eigvals(A)
sI_A = np.poly1d(eig, True, variable='s')

alpha = np.round(sI_A)
alpha = alpha[::-1]

np.linalg.eigvals()は引数の固有値をnumpy.ndarrayで返します．

np.poly1d()は，第1引数に係数または根を渡し，
第2引数にTrueとすると根にFalseとすると係数になります.
variableは$s$としておきました．デフォルトでは$x$のようです．

sI_Aをprintするとわかりますが，係数はきれいな整数値にならないことがあります．
なので，np.round()で整数値に変換します．
この時点では，$\alpha$は降べきの順の係数になっているので，
alpha[::-1]で逆順にします．

可観測行列$U_o$を求める


Uo = np.array(c)
for i in range(dim - 1):
    if i == 0:
        temp =c
    else:
        temp = Uo[i,:]
    Uo = np.vstack((Uo, np.dot(temp, A)))

rank_Uo = np.linalg.matrix_rank(Uo)

可観測行列をつくっていきます．まずは，cを登録します．
その後，$cA$, $cA^2$ $\cdots$をnp.vstack()で行を追加していきます．
内積はc*Aではなく，np.dot()なので注意してください．

最後に，np.linalg.matrix_rank()で可観測行列のランクを求めておきます．
これを元に，if文にしてオブザーバを設計可能か否かを判別してもよかったのですが，
今回はとりあえず，rankを表示するにとどめました．

行列Vを求める


V = np.zeros((dim, dim))
for y in range(dim):
    for x in range(dim):
        if x + y < dim - 1:
            V[y,x] = alpha[x+y+1]
        elif x + y == dim - 1:
            V[y,x] = 1

変換行列を求めるための行列Vを求めます．
まずは，$n次元 \times n次元$のゼロ行列を作成します．
その後，$x$方向(行方向)と$y$方向(列方向)に対してfor文を回し，
行列の斜め方向で値は等しいので，$x+y$の値に応じて
alpha[]を参照させます．
右下三角行列の要素は$0$なので$x+y$が次元dim-1より大きくなったところは
特に値を書き換える必要はありません．

変換行列Tを求める


To = np.dot(V, Uo)
To_inv = np.linalg.inv(To)

np.dot()で変換行列を求めます．
また，その逆行列も必要なので，np.linalg.inv()で求めておきます．

オブザーバゲインを求める


p_s = np.poly1d(new_pole, True, variable='s')

beta = np.round(np.array(p_s))
beta = beta[::-1]

a_b = alpha-beta
a_b = np.delete(a_b, dim, 0)
a_b = np.reshape(a_b, (dim, 1))

k = np.dot(To_inv, a_b)

最後に，オブザーバゲインを求めにかかります．
前半部分はalphaを求めたところと何ら変わりはありません．

alpha-betaの最後の要素は必要ないので，np.delete()で削除します．
この時点ではa_bは横ベクトルなのでreshape()で縦ベクトルに整形します．
あとは，内積を取ってオブザーバゲインが求まります．

まとめ

いかがだったでしょうか？とてもいい行列操作の練習になったのではないかと思います．
コードに関して改善点や気になった点などあればコメントからお願いします！

【制御工学】オブザーバの設計を行うプログラムをつくってみた！

概要

動作環境

オブザーバ

コード

解説

まとめ