Deep Learning 教師あり学習の入門的な内容として、MLP、CNN、RBMについて3回に分けて投稿する予定です。第一回目の今回は、MLPについてまとめます。MLPについて触れる前に、まずは、マカロック・ピッツの素子モデル ( 以下、マカロック・ピッツモデルと表記 ) と単純パーセプトロンについて見ていきます。
McCulloch-Pitts (MCP) neuron
マカロック・ピッツモデルは、神経細胞を模倣した最初のモデルであり、1943 年に Warren Sturgis McCulloch と Walter J. Pitts により発表されました。このモデルでは、次のように神経細胞の機能を単純化しています。
- 神経細胞の膜電位は、活動電位が引き起こされた状態 ( 1 ) と静止膜電位の状態 ( 0 ) の 2 値をとる。
- 活動電位は軸索を通じて、それに繋がっている他の神経細胞へ興奮刺激として伝搬する。
- 神経細胞の膜電位は、軸索末端がそれに繋がる他の神経細胞から受け取る興奮刺激の総和により変化する。
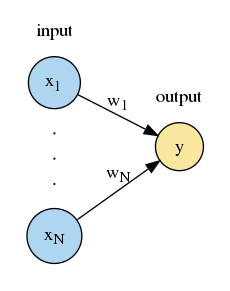
上図は出力が 1 個のマカロック・ピッツモデルを表しており、丸が神経細胞、$x_1,\cdots,x_N,y$ がその神経細胞の膜電位を表しています。以下、$\boldsymbol{x}=\left(x_1,\cdots,x_N\right)$ を入力、$y$ を出力と呼びます。このモデルにおいて、出力 $y$ は次のように表されます。
y=f\left(\boldsymbol{w}\boldsymbol{x}^\top-h\right)\in\{0,1\}
ここで、
\begin{array}{l}
x_{i}\in\{0,1\}\text{ for }i\in\{1,\cdots,N\}\\
\boldsymbol{w}=(w_1,\cdots,w_N)&:\text{結合重みベクトル} \\
h&:\text{閾値}\\
f(u)=\left\{\begin{array}{l}1,&u\ge0\\0,&u<0\end{array}\right.&:\text{活性化関数}
\end{array}
です。$w_i$ は $i$ 番目の入力神経細胞の活動電位が、どの程度の強さで出力神経細胞に伝えられるかを表すパラメータです ( $i\in\{1,\cdots,N\}$ ) 。マカロック・ピッツモデルでは活性化関数にヘヴィサイドの階段関数を用いるため、出力神経細胞が受け取る刺激の総和が閾値 $h$ を超えると出力神経細胞の活動電位が引き起こされます。このモデルでは、$\boldsymbol{w}$ や $h$ の値は解く問題に合わせて人の手で設定されます。学習サンプルから自動的にパラメータの値が決定されるようにマカロック・ピッツモデルを修正したものが、次の単純パーセプトロンです。
Perceptron ( Single-layer perceptron )
単純パーセプトロンは、1958 年に Frank Rosenblatt によって発表されました。前述のマカロック・ピッツモデルにおいては神経細胞と読んでいたものを、( 人工ニューラルネットワークで扱う仮想化した神経細胞のことをパーセプトロンと呼ぶことがありますが、単純パーセプトロンのアルゴリズムを単にパーセプトロンと呼ぶこともあるため、語弊を招かないように ) これ以降ユニットと呼びます。このモデルは、マカロック・ピッツモデルにおけるパラメータ $\boldsymbol{w}$、 $h$ が自動的に学習されるように改良したモデルで、トレーニングデータ・セット $D=\{(\boldsymbol{x}_1,t_1),\cdots,(\boldsymbol{x}_S,t_S)\}$ を用いてパラメータを学習します。ここで、$t_s$ は入力 $\boldsymbol{x}_s$ に対して要求される出力値です ( $s\in\{1,\cdots,S\}$ )。以下、マカロック・ピッツモデルの説明で用いた図で表されるような、入力層に $N$ 個、出力層に 1 個のユニットがあるモデルを例に取り、パラメータが学習されるアルゴリズムを説明します ( 記号の意味も前節と同じです ) 。
Step 1. パラメータ $\boldsymbol{w}$、 $h$ を ( 乱数で ) 初期化する。
Step 2. $(\boldsymbol{x}_s,t_s)\in D\text{ for all }s$ に対して、次を行う。
$\qquad$Step 2-1. 入力 $\boldsymbol{x}_s$ に対する出力 $y_s$ を計算。
y_s=f\left(\boldsymbol{w}\boldsymbol{x}_s^\top-h\right)\in\{0,1\}
$\qquad$Step 2-2. パラメータ $\boldsymbol{w}$、 $h$ を更新 ( 誤り訂正学習 ) 。$\eta$ は学習率を表す。
\begin{array}{l}
\boldsymbol{w}+\eta\left(t_s-y_s\right)\boldsymbol{x}\to\boldsymbol{w}\\
h-\eta(t_s-y_s)\to h
\end{array}
Step 3. 終了条件を満たすまで Step 2 を繰り返す。
単純パーセプトロンは、入力層と出力層の 2 層構造のため、線形分離可能な問題しか解くことが出来ないと 1969 年に Marvin Minsky と Seymour Papert により指摘されました。この問題を解決したのが、次に説明する多層パーセプトロンです。
Multilayer perceptron ( MLP )
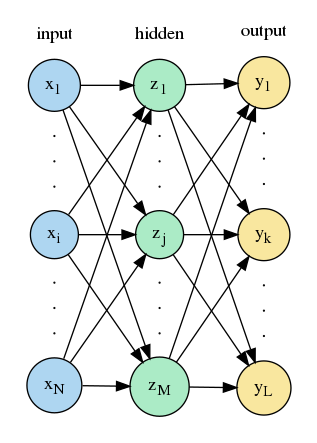
多層パーセプトロンは、ユニットの層を 3 層以上持つ人工ニューラルネットワークです。1986 年に David E. Rumelhart 等によって発表された誤差逆伝播法を用いることで、ユニットの層を3層以上重ねたモデルでも自動でパラメータを学習させることが可能になり、線形分離不可能な問題も解くことが出来るようになりました。以下では、上図に示す隠れ層が 1 層の多層パーセプトロンを説明します。入力 $\boldsymbol{x}$ が与えられたとき、隠れ層の状態 $\boldsymbol{z}$ と出力層の状態 $\boldsymbol{y}$ は次のように表されます。
\begin{array}{l}
\boldsymbol{z}=\left(1,f^{(1)}\left(z'_1\right),\cdots,f^{(1)}\left(z'_M\right)\right),\;\left(z'_1,\cdots,z'_M\right)=\boldsymbol{z'}=\boldsymbol{x}W^{(1)}\\
\boldsymbol{y}=\left(f^{(2)}\left(y'_1\right),\cdots,f^{(2)}\left(y'_L\right)\right),\;\left(y_1,\cdots,y'_L\right)=\boldsymbol{y'}=\boldsymbol{z}W^{(2)}
\end{array}
ここで、
\begin{array}{l}
\boldsymbol{x}=\left(x_0,x_1,\cdots,x_N\right),\;x_0=1&:\text{入力ベクトル。}x_1,\cdots,x_N\text{ が実際の入力で、}\\
&\phantom{:}x_0\text{ はバイアスを結合重み行列の要素として表現するために便宜的に導入した値です。}\\
\boldsymbol{z}=\left(z_0,z_1,\cdots,z_M\right),\;z_0=1&:\text{隠れ層の出力ベクトル。}\\
&\phantom{:}x_0\text{ と同様に }z_0\text{ も便宜的に導入した値です。}\\
\boldsymbol{y}=\left(y_1,\cdots,y_L\right)&:\text{出力ベクトル}\\
W^{(1)}=\left(w^{(1)}_{ij}\right)_{\begin{array}{l}0\le i\le N\\1\le j\le M\end{array}}&:\text{入力層と隠れ層間の結合重み行列。}\\
W^{(2)}=\left(w^{(2)}_{jk}\right)_{\begin{array}{l}0\le j\le M\\1\le k\le L\end{array}}&:\text{隠れ層と出力層間の結合重み行列。}\\
f^{(1)},\;f^{(2)}&:\text{微分可能な活性化関数}
\end{array}
です。$j\in\{1,\cdots,M\}$、$k\in\{1,\cdots,L\}$に対して、
\begin{align}
z_j=f^{(1)}\left(w^{(1)}_{0j}+\sum_{i=1}^{N}x_iw^{(1)}_{ij}\right)\\
y_k=f^{(2)}\left(w^{(2)}_{0k}+\sum_{l=1}^{M}z_lw^{(2)}_{lk}\right)
\end{align}
であり、$w^{(1)}_{ij}$ は入力層 $i(\ne 0)$ 番目と隠れ層 $j$ 番目のユニット間の結合重み、$w^{(2)}_{jk}$ は隠れ層 $j(\ne 0)$ 番目と出力層 $k$ 番目のユニット間の結合重みを表します。また、$w^{(1)}_{0j}$と$w^{(2)}_{0k}$はそれぞれ、隠れ層 $j$ 番目、出力層 $k$ 番目のユニットのバイアスを表します。トレーニングデータ・セット $D=\{(\boldsymbol{x}_1,\boldsymbol{t}_1),\cdots,(\boldsymbol{x}_S,\boldsymbol{t}_S)\}$ が与えられたとき、逐次的に多層パーセプトロンが結合重み $W^{(1)}$、$W^{(2)}$ を学習するアルゴリズムを以下に記します。
Step 1. $W^{(1)}$、 $W^{(2)}$ を ( 乱数で ) 初期化する。
Step 2. $(\boldsymbol{x}_s,\boldsymbol{t}_s)\in D \text{ for all }s$ に対して、次を行う。
$\qquad$Step 2-1. 入力 $\boldsymbol{x}_s$ に対して $\boldsymbol{z}_s$、$\boldsymbol{y}_s$ を計算。
\begin{array}{l}
\boldsymbol{z}_s=\left(1,f^{(1)}\left(z'_{s,1}\right),\cdots,f^{(1)}\left(z'_{s,M}\right)\right),\;\left(z'_{s,1},\cdots,z'_{s,M}\right)=\boldsymbol{z'}_s=\boldsymbol{x}_sW^{(1)}\\
\boldsymbol{y}_s=\left(f^{(2)}\left(y'_{s,1}\right),\cdots,f^{(2)}\left(y'_{s,L}\right)\right),\;\left(y'_{s,1},\cdots,y'_{s,L}\right)=\boldsymbol{y'}_s=\boldsymbol{z}_sW^{(2)}
\end{array}
$\qquad$Step 2-2. 損失関数 $E_s\left(\boldsymbol{y}_s,\boldsymbol{t}_s\right)$ を用いて、$W^{(1)}$、 $W^{(2)}$ を更新 ( 最急降下法 ) 。
\begin{align}
W^{(1)}+\left(\Delta w^{(1)}_{ij}\right)\to W^{(1)},\;\Delta w^{(1)}_{ij}=-\eta\frac{\partial E_s}{\partial w^{(1)}_{ij}}\\
W^{(2)}+\left(\Delta w^{(2)}_{jk}\right)\to W^{(2)},\;\Delta w^{(2)}_{jk}=-\eta\frac{\partial E_s}{\partial w^{(2)}_{jk}}
\end{align},\;\text{ for all }i,j
Step 3. 終了条件を満たすまで Step 2 を繰り返す。
損失関数として使われるものの幾つかを以下に上げます。
\begin{array}{l}
E_s=\frac{1}{L}\sum_{k=1}^{L}\left(t_{s,k}-y_{s,k}\right)^2&:\text{mean square error}\\
E_s=-\sum_{k=1}^{L}t_{s,k}\mathrm{log}\left(y_{s,k}\right)&:\text{(multinomal) cross entropy}\\
E_s=\sum_{k=1}^{L}t_{s,k}\mathrm{log}\left(\frac{t_{s,k}}{y_{s,k}}\right)&:\text{kullback leibler divergence}\\
E_s=\frac{1}{L}\sum_{k=1}^{L}\mathrm{log}\left\{\mathrm{cosh}\left(t_{s,k}-y_{s,k}\right)\right\}&:\text{logarithm of the hyperbolic cosine}
\end{array}
データ $(\boldsymbol{x},\boldsymbol{t})$ に対して得られる損失 $E(\boldsymbol{y},\boldsymbol{t})$ を用いて ( 以下、何番目のデータかを表す付き文字の $s$ は省略しています )、 Step 2-2 中の偏微分は次のように計算されます。
\begin{align}
\frac{\partial E}{\partial w^{(2)}_{jk}}&=\sum_{k'=1}^{L}\frac{\partial E}{\partial y_{k'}}\frac{\partial f^{(2)}\left(y'_{k'}\right)}{\partial y'_{k'}}\frac{\partial y'_{k'}}{\partial w^{(2)}_{jk}}\\
&=\frac{\partial E}{\partial y_k}\frac{\partial f^{(2)}\left(y'_k\right)}{\partial y'_k}z_j\\
&=\delta^{(2)}_kz_j,\qquad\delta^{(2)}_k=\frac{\partial E}{\partial y_k}\frac{\partial f^{(2)}\left(y'_k\right)}{\partial y'_k}\\\\
\frac{\partial E}{\partial w^{(1)}_{ij}}&=\sum_{k=1}^{L}\frac{\partial E}{\partial y_k}\frac{\partial f^{(2)}\left(y'_k\right)}{\partial y'_k}\frac{\partial y'_k}{\partial w^{(1)}_{ij}}\\
&=\sum_{k=1}^{L}\frac{\partial E}{\partial y_k}\frac{\partial f^{(2)}\left(y'_k\right)}{\partial y'_k}\sum_{j'=1}^{M}w^{(2)}_{j'k}\frac{\partial f^{(1)}\left(z'_{j'}\right)}{\partial z'_{j'}}\frac{\partial z'_{j'}}{\partial w^{(1)}_{ij}}\\
&=\sum_{k=1}^{L}\frac{\partial E}{\partial y_k}\frac{\partial f^{(2)}\left(y'_k\right)}{\partial y'_k}w^{(2)}_{jk}\frac{\partial f^{(1)}\left(z'_j\right)}{\partial z'_j}x_i\\
&=\delta^{(1)}_jx_i,\qquad\delta^{(1)}_j=\frac{\partial f^{(1)}\left(z'_j\right)}{\partial z'_j}\sum_{k=1}^{L}\delta^{(2)}_kw^{(2)}_{jk}
\end{align}
今は 3 層からなる多層パーセプトロンについて説明していますが、層が $R(\ge 3)$ 層ある場合、次が成り立ちます。
\begin{align}
&\frac{\partial E}{\partial w^{(r)}_{mn}}=\delta^{(r)}_nx^{(r)}_m\;\text{ for }r\in\{1,\cdots,R-1\},\quad m\in\{0,\cdots,N_{r}\},\;n\in\{1,\cdots,N_{r+1}\}\\
&\delta^{(R-1)}_k=\frac{\partial E}{\partial x^{(R)}_k}\frac{\partial f^{(R-1)}\left(x'^{(R)}_k\right)}{\partial x'^{(R)}_k},\quad k\in\{1,\cdots,N_{R}\}\\
&\delta^{(r)}_i=\frac{\partial f^{(r-1)}\left(x'^{(r)}_i\right)}{\partial x'^{(r+1)}_i}\sum_{j=1}^{N_{r+2}}\delta^{(r+1)}_jw^{(r+1)}_{ij}\;\text{ for }r\in\{1,\cdots,R-2\},\quad i\in\{1,\cdots,N_{r+1}\}
\end{align}
ここで、$r$ 層目のユニットの総数を $N_r$ としています ( $r\in\{1,\cdots,R\}$ )。また、
\begin{align}
&\begin{array}{l}
x^{(r)}_k&:\text{$r$ 層 $k$ 番目のユニットの状態。}\\
&\phantom{:}\text{ここで、}
\left\{\begin{array}{l}
r\ne R\text{ のとき、}k\in\{0,1,\cdots,N_r\}\text{ かつ }x^{(r)}_0=1\\
r=R\text{ のとき、}k\in\{1,\cdots,N_r\}
\end{array}\right.\\
W^{(r)}=\left(w^{(r)}_{ij}\right)_{\begin{array}{l}0\le i \le N_r\\1\le j \le N_{r+1}\end{array}}&:\text{$r$ 層と $r+1$ 層間の結合重み行列。}\;r\in\{1,\cdots,R-1\}\\
f^{(r-1)}&:\text{$r$ 層目のユニットの ( 微分可能な ) 活性化関数}
\end{array}\\
&x'^{(r)}_k=\sum_{l=0}^{N_{r-1}}w^{(r-1)}_{lk}x^{(r-1)}_l,\;\left(w^{(r-1)}_{lk}\right)=W^{(r-1)}\\
\end{align}
です。以上のように $r$ が大きい順に ( 出力層から入力層方向へ ) $\delta^{(r)}_k$ を計算し、各層間の結合重みを最急降下法で更新する方法を誤差逆伝播法と呼びます。多層パーセプトロンでは、活性化関数の選び方によっては、層の数を増やすほど $r$ が 1 に近い $\delta^{(r)}_k$ の値が $0$ に収束してしまう問題が生じます ( 勾配消失問題 ) 。この解決策として、活性化関数に rectified linear unit ( ReLU ) を使うという方法があります。
\begin{array}{l}
f(u)=\mathrm{max}\left\{0,u\right\}&:\text{ReLU}
\end{array}
ReLU の 1 回微分は引数の値が正であれば 1 なので、層の数を増やしても、活性化関数の微分の累積により 損失関数の勾配が消失するという問題が生じません。