Pythonで数学の勉強：確率の簡単な問題を解く

確率

Python関係ないだろって問題もあるが、
計算機あってよかったと思える設定にして解く。

(問1)

ジョーカーを除く52枚のトランプからプレイヤーは1枚抜き出し裏向きに置いた。
ディーラーが残りの山からランダムに3枚抜き出し表向けにすると全てダイヤであった。

1. トランプの製造元の人が来て今使っているトランプはハートのAの変わりにダイヤのAが重複して入っている不良品であると教えてくれた。最初に抜き出したカードがダイヤである確率を求めよ。
2. 追加の情報としてディーラーはガン付けを行ってダイヤだけを作為的に抜き出していたことがわかった。最初に抜き出していたカードがダイヤである確率を求めよ。

(解)

1. 条件付き確率の問題。

P_0 = sym.Rational(1, 4)
P_0dia = sym.Rational(13*12*11, 51*50*49)
P_dia = sym.Rational(14*13*12, 52*51*50)
P_0 * P_0dia / P_dia

$$\frac{143}{686}$$
2. $$\frac{7}{26}$$

(問2)

当たる確率が$p$であるくじがある。
地球上の人全てが1回ずつくじを引くとして全てハズレる確率が0.5以上となるには
$p$はいくらぐらいでないといけないか。
地球の人口は72億人とせよ。

(解)
ポアソン分布で近似する。

N = 7200000000
F = sym.exp(-p*N) - 0.5
sym.solve([F], [p])

$$p < 9.627 \cdot 10^{-11}$$

ちなみにこのぐらいの試行を行うと正規分布だと標準偏差の7倍ほど、
パレート分布では1億倍以上離れた値が出てもおかしくない。

(問3)

1. 壺の中に赤玉が12個、黒玉が8個入っている。3個の玉を取り出したときに赤玉2個である確率を求めよ。
2. 赤玉が$4 \cdot 10^{24}$個、黒玉が$2 \cdot 10^{24}$個入っていて$3 \cdot 10^{24}$個取り出すという試行を行う。
   取り出される赤玉が$2 \cdot 10^{24}$個である確率を求めよ。
3. (2)の試行を行う時、取り出された赤玉の個数と$2 \cdot 10^{24}$との差の絶対値を$x$とする。
   結果が$x$以下になる確率を$P_x$とするとき、$P_x>0.5$となるのは$x$がいくらぐらいか。

(解)

1. これは超幾何分布と呼ばれる。

import sympy as sym
A = sym.functions.combinatorial.numbers.nC(12, 2)
B = sym.functions.combinatorial.numbers.nC(8, 1)
C = sym.functions.combinatorial.numbers.nC(20, 3)
A*B/C

$$\frac{44}{95}$$
2. アボガドロ数に近い個数を設定した。統計力学よりの問題。
超幾何分布の定義より、
$$
\begin{eqnarray}
P &=& \frac{C(4 \cdot 10^{24}, 2 \cdot 10^{24}) \cdot C(2 \cdot 10^{24}, 10^{24})}{C(6 \cdot 10^{24}, 3 \cdot 10^{24})} \\
&=& \frac{(4 \cdot 10^{24})!{(3 \cdot 10^{24})!}^2}{(6 \cdot 10^{24})!(2 \cdot 10^{24})!{(10^{24})!}^2}
\end{eqnarray}$$
$\log(n!)\eqsim n\log n -n + \frac{1}{2} \cdot \log(2\pi n)$の近似を用いる。

log_n = n * sym.log(n) - n + sym.log(2 * Pi * n) / 2
A1 = log_n.subs([(n, 4*10**24)])
A2 = log_n.subs([(n, 3*10**24)])
B1 = log_n.subs([(n, 6*10**24)])
B2 = log_n.subs([(n, 2*10**24)])
B3 = log_n.subs([(n, 1*10**24)])
Log_P = A1 + 2 * A2 - B1 - B2 - 2 * B3
sym.N(Log_P, 10)

$−28.0006535$
$$\therefore P \simeq e^{-28} \simeq 6.9144 \cdot 10^{-13}$$
3. 赤玉の個数$X$は二項分布$B(3*10^{24}, 2/3)$で近似される。
さらに正規分布で近似すると、
$$Y = \frac{X-2\cdot 10^{24}}{\sqrt{3 \cdot 10^{24}\cdot 2/3 \cdot 1/3}}\\
= \sqrt{\frac{3}{2}} \frac{X-2 \cdot 10^{24} }{10^{12}}$$
$Y$は標準正規分布に従う。累積密度が0.5を超えるのは標準正規分布表から、
$-0.68<Y<0.68$
$X=2 \cdot 10^{24} \pm 0.68 \cdot \sqrt{\frac{2}{3}} 10^{12}$
$x \simeq 5.55 \cdot 10^{11}$

(問4)

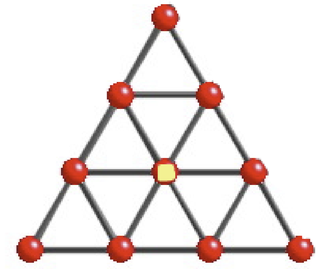
図の三角格子の中央黄色の部分からスタートして1秒ごとに隣接格子に等確率に移動するランダムウォークを考える。
$t$秒後に中央にいる確率を$P_t$とする。

1. $P_{10}$を求めよ。
2. $\lim_{n \to \infty}P_n$を求めよ。

(解)

1. 対称性から距離1の各点にいる確率を$Q_t$、距離2の各点にいる確率を$R_t$とおくと、
   $$P_t+6Q_t+3R_t=1$$

N = 1
P = 0
Q = sym.Rational(1, 6)
R = 0
Pn = sym.Rational(3, 2) * q
Qn = p/6 + q/2 + r/2
Rn = q/2
while N < 10:
    N += 1
    Ptemp = Pn.subs([(q, Q)])
    Qtemp = Qn.subs([(p, P), (q, Q), (r, R)])
    Rtemp = Rn.subs([(q, Q)])
    P = Ptemp
    Q = Qtemp
    R = Rtemp
print(N)
print(P)
print(Q)
print(R)

$10$
$171/1024$
$341/3072$
$57/1024$
2.

F1 = sym.Rational(3, 2) * q - p
F2 = p/6 + q/2 + r/2 - q
F3 = q/2 - r
Ft = p + 6*q + 3*r - 1
sym.solve([F1, F2, F3, Ft], [p, q, r])

$$\left \{ p : \frac{1}{6}, \quad q : \frac{1}{9}, \quad r : \frac{1}{18}\right \}$$

(問5)

0～65535の範囲の整数の一様乱数を$n$個発生させるとする。

1. 同じ乱数が含まれる確率が0.5を超える$n$の値を求めよ。
2. 同じ乱数が3つ以上含まれる確率が0.5を超える$n$の値を求めよ。

(解)

1. バースディアタックである。

def birthday(N, K):
    return sym.functions.combinatorial.numbers.nP(N, K)/N**K
N = 65536
K = 255 # 平方根ぐらいから始めればいい
P = 0.0
while P <= 0.5:
    K += 1
    P = 1 - birthday(N, K)
print(K)
sym.N(P, 10)

$302$
$0.5007224895$
2. $N$種の乱数$K$個の中に同じ乱数が2個含まれる組み合わせは、

$$\sum_{k=1}^{K/2} C(N-k,k)P(N,K-k)$$
$K/2$の境界部分は大した影響を与えないので気にせず足してみる。

def birthday2(N, K, P1):
    return (sym.functions.combinatorial.numbers.nP(N,K) + P1) / N**K
def P1(N,K,X):
    return sym.functions.combinatorial.numbers.nC(N-X,X)*sym.functions.combinatorial.numbers.nP(N,K-X)
N = 65536
K = 300
P = 0.0
while P <= 0.5:
    K += 1
    L = 1
    SUM = 0
    while L <= K/2:
        SUM += P1(N, K, L)
        L += 1
    P = 1 - birthday2(N, K, SUM)
print(K)
sym.N(P, 10)

$473$
$0.5035181768$