Google Apps Scriptで配列要素の総和処理を高速で行いたい

概要

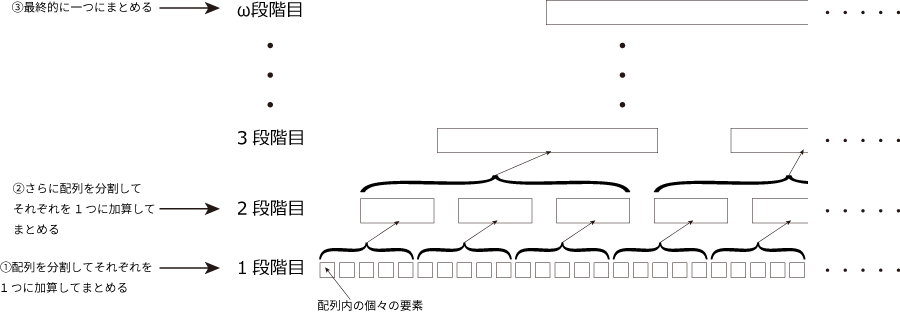
$\hspace{1em}$ Google Apps Script（GAS）における配列要素の総和について、従来よりも効率的な手法について投稿します。この記事の方法を使用すると配列内の全要素を足し合わせる際の処理時間を早めることができます。下記表1は配列の要素数が100万で各要素は2要素の1次元配列で中身は文字列とし、この全要素を総和処理するときの従来の手法と今回報告する手法との処理時間の違いを示しています。この記事で報告する方法は配列の各要素を総和処理する内容です。この方法では、ピラミッドを登るように要素をグループ毎に分割しながら加算していくことで、スクリプト内で扱う総データ量が少なくなり、結果として処理速度の改善に至りました。（図1）

表1: 配列要素の総和における従来方式と本記事の手法（ピラミッド方式）との処理時間の比較. 配列の要素は文字列.

配列要素数	各要素のサイズ	従来方式での総和処理時間	ピラミッド方式での総和処理時間
1,000,000個	10バイト	約52分	約8秒

図1. 総和処理のためのピラミッド方式のイメージ図.

経緯

$\hspace{1em}$ ここでは本投稿で報告する図1のイメージ図にある総和処理の方法について、なぜこの方法を考えることになったかという理由と、この方法に至るまでの思考の流れについて自分へのメモも兼ねて記載します。

少し前からGoogle Apps Script（GAS）を使って外部から取り込んだデータをスプレッドシートへ保存、解析を行っていました。最近になってローカルで別の解析を行うためにデータをCSVデータとして保存する必要がでてきました。いつもは下記のような従来の方法でデータを整形してCSVファイルを出力するのですが、

    Declare a string variable arr, sum
    Declare an integer variable loopcounter
    Set arr to size n
    for loopcounter = 0 to (size of arr) - 1
        sum = sum + arr[loopcounter]
        loopcounter = loopcounter + 1
    endfor

今回はデータ量が数十万行から最大で100万行程度と多いため、ここで初めて配列要素の総和に多くの時間がかかることに気付きました。個々の要素は2要素の1次元配列です。ローカルでは特に要素数100万程度の総和処理は気にならない時間で終わっていましたので軽い気持ちでGASで行ったところ厳しい結果になりました。

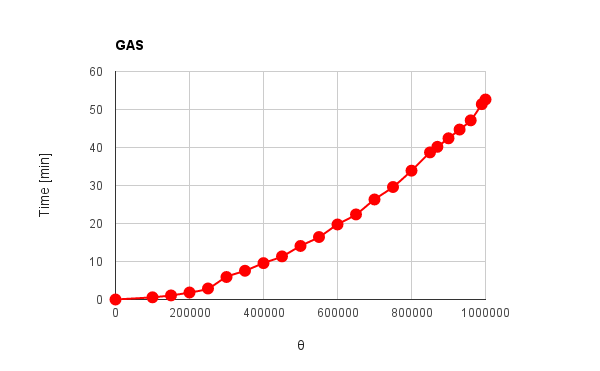
図2. GASで配列要素を総和処理するときの要素数$\theta$と処理時間の関係.

図2は全要素数100万の配列を総和したときの要素数$\theta$に対する処理時間を示しています。22万程度の要素数でGASの実行時間の上限である6分（2016/10/13現在）を超えてしまいます。このため、処理時間の測定には要素数100万の配列の総和を実行時間の制限内におさまるように分割し、それらを順に足し合わせたときの処理時間を記録しました。具体的には最初に100,000要素まで総和し、そのデータと処理時間をそれぞれテキストファイルへ出力します。次に起動するときに前回のデータを変数へ読み込み、そこへ続きとして100,000から110,000要素の配列を順に足し合わせて結果をテキストファイルへ出力するといった流れで要素数100万まで進めました。実行にはトリガーを用いて十分時間を空けて行いました。総和処理に用いたスクリプトの基本は上記の疑似コードで示した従来法で行っています。何かミスをしているのではと思い、スクリプトを再確認しましたが問題は見つからず、残念ながら100万要素の総和処理を制限時間の6分以内に終わらせるには至りませんでした。

総和処理に相当の時間を要するため初めはスクリプト内で総和せずに配列のままスプレッドシートへ展開し、手動でCSVへ出力してダウンロードという流れで行っていましたが定期的にこれを行うには少し手間に感じていました。もしもGoogle上でCSV出力用の専用APIがあったり、すぐに効果的な方法が見つかっていたのなら今回の方法は思いつかなかったと思います。元になるデータ取得時にCSV形式でファイルへ直接保存するのもあり？とも思ったのですが、これについては諸々の事情によりスプレッドシートからCSVデータへ変換する必要がありました。残念ながら待っていても解決することは難しいと判断して、GASを用いて最大100万の配列について、総和処理を実行時間の上限である6分以内にすることを目的にしてその解決策を考えました。これが、文字列を要素とする配列要素の総和処理について従来法よりも効率的な方法の提案につながりました。次のセクションではスクリプトを組む前に行った思考実験について記載します。

思考実験

$\hspace{1em}$ ここでは実験用スクリプト作成までに行った思考実験の内容について記載します。最初に従来法で得た図2をよく見るところから始めました。図2を見ると100万要素を加算しているとき各要素での処理時間がリニアに増加していないことが分かります。横軸を対数にすると直線状になります。すなわち要素数に対して指数関数的に増加しています。今の場合、配列要素数の二乗に比例して増加しています。そこで、処理時間を改善するために総和処理中にデータがどのように動いているかについて考えることにしました。前セクションで示したスクリプトから実行中のデータの動き（sumのサイズの動き）を計算します。配列の各要素を$\mu$ bytes、要素数$\theta$を持つ配列内の全要素を従来法で足し合わせる場合、sumに代入される総データ量$\Psi$は次のように表現できます。

\Psi = \sum_{\lambda=1}^{\theta} \mu \lambda \tag{1}

図3. 式(1)を図示.

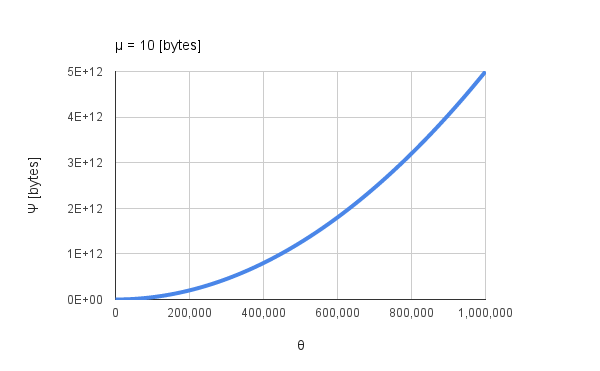
式$(1)$を図示した図3を見ると、$\Psi$は要素数$\theta$の二乗に比例して増加していることが分かります。これは図1の傾向と一致しています。総和処理中の状況を想像してみると、例えば各要素が2要素の1次元配列（区切り、改行コードを含めると10バイト）を持つ要素数100万個の配列を全て足し合わせる場合、99万番台を処理するときには10 MBytes程度の変数への加算が1万回続くことになります。式(1)から、総和処理中に動いている全データ量（上記疑似コードのsumの総計）は$5 \times 10^{12}$ bytesになります。これはとても大きいのではないかと考えました。

このフローのビジョンを想像しながら、大きなデータ量でのループを少なくするにはどのようにすべきかと考えていると、自分の中のイメージとして、横に加算するよりも縦に加算してはどうかとの仮説に至りました（この部分は文章として表現し難くて申し訳ありません）。これを目で見えるようにすると概要セクションで示した図1のようになります。各要素を順に足し合わせるのではなく、グループごとに分割して足し合わせ、それらのグループ群をさらにグループに分けて足し合わせてグループ数を減少させていくような、ピラミッドを登っていくような型の総和処理にすることで処理中に動くデータ量を小さくすることができるのではないかと考えました。その効果として処理速度を向上させることができるのではないかと考えました。次に仮説がどの程度正しい方向を向いているか知るために紙とペンを使用しました。

ここで、できるだけシンプルに考えたいので系を定義します。このような定義（制限）は多くのパラメータが関与しているような系では重要です。トレンドを確認しつつ必要であれば次の段階でこの制限を緩めていきます。

1. 目標である配列要素数1,000,000に対しての処理速度改善なのでこれを固定

2. 分割サイズは各段階で固定

3. 配列の個々の要素は ['0000000', 'a'] の1次元配列の文字列とし、これをカンマで区切って足し合わせ、最終端に改行コードとして'\n'を付けることでサイズを文字列10バイトに固定

配列要素数、各要素のサイズは私自身の事情によりますが、仮説が正しい方向を向いているかの定性的な確認にはこれでも問題ないと考えました。

配列要素数を$\theta$, 1要素当たりのデータサイズを$\mu$, 分割サイズを$\phi$, 段階数（ピラミッドを登る階数）を$\omega$として図1を考えます。データの動きを見やすくするために$\omega=1$での疑似コードを用意しました。$\omega=0$は先に述べた従来方法に当たります。

    Declare a string variable arr, tempsum, sum
    Declare an integer variable division, loopcounter1, loopcounter2
    Set arr to size n
    division = d
    for loopcounter1 = division to (size of arr) - 1
        for loopcounter2 = 0 to (size of arr) - 1
            tempsum = tempsum + arr[loopcounter2]
            loopcounter2 = loopcounter2 + 1
        endfor
        sum = sum + tempsum
        tempsum = ''
        loopcounter2 = loopcounter1
        loopcounter1 = loopcounter1 + division
    endfor

この疑似コードでのデータの動きは主に変数に代入される部分、すなわちtempsum, sumについてデータがどのように動くのかを考えます。この疑似コードは1段階だけですが、このコードを見ながら$\omega$段階まで分割していくときのデータの動き、すなわち全データ量$\Psi(\omega)$は次のように表現することができます。実際に作成したライブラリで全データ量を出力させると下記式で得た結果と同じ結果を得ています。

\left(\sum_{\lambda=1}^{\phi_1} \mu_{1} \lambda\right)\frac{\theta_{1}}{\phi_{1}} +
\left(\sum_{\lambda=1}^{\phi_2} \mu_{2} \lambda\right)\frac{\theta_{2}}{\phi_{2}} +
 \cdots

\cdots +
\left(\sum_{\lambda=1}^{\phi_{\omega-1}} \mu_{\omega-1} \lambda\right)\frac{\theta_{\omega-1}}{\phi_{\omega-1}} +
\left\{\left(\sum_{\lambda=1}^{\phi_{\omega}} \mu_{\omega} \lambda\right)\frac{\theta_{\omega}}{\phi_{\omega}} + \sum_{\lambda=1}^{\frac{\theta_{\omega}}{\phi_{\omega}}} \mu_{\omega}\phi_{\omega}\lambda  \right\}
 \tag{2}

$\omega$段目は最後に残った要素を足し合わせるため他とは少し異なりますので注意してください。

ここで、

\theta_{\omega} = \frac{\theta}{\phi^{\omega-1}}

\mu_{\omega} = \mu\phi^{\omega-1}

となるので上記の式を整理してまとめると、

\Psi(\phi, \omega) = \frac{\mu\theta}{2}\left\{ \left(\phi + 3\right)\omega + \frac{\theta}{\phi^{\omega}} - 1 \right\} \tag{3}

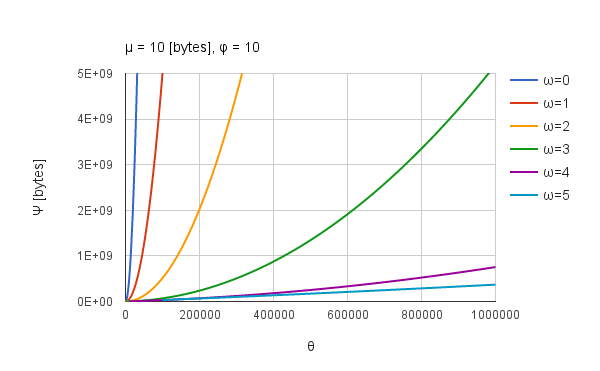
のようにシンプルに展開できます。この式から、ピラミッド方式によって総データ量$\Psi$が要素数$\theta$に対してどのように変化するかを図示して確認することができます。$\mu=10, \phi=10$とすると図4のようになります。

図4. 式(3)を図示.

図4中の$\omega=0$は従来法です。$\theta$が0から100万の間でみると、段階数$\omega$が増加するほど横軸に近づいていく（傾きが小さくなる）とともに変化のしかたが直線状に近づいていることが認められます。このことから、思考実験の方向性は間違いではなさそうだということと、ピラミッド方式を採用することで総和の処理時間を短縮できる可能性がより高くなったと考えました。また、従来法では総データ量$\Psi$は要素数増加に伴って要素数の二乗に比例して大きくなりますので、素直に考えると処理時間も要素数の二乗に比例して増加すると考えられます。これは図2と一致しているといえます。この傾向から、ピラミッド方式で総和処理を行うと、その処理時間の変化は要素数$\theta$に対して直線状の変化を示すのではないかとも考えられます。もしも従来法を用いた処理で図4の傾向から外れる場合、すなわち、リニアに近づく場合はスクリプト実行時に何らかの最適化が行われていると言えるのかもしれません。

次に式$(3)$を使って処理中に動くデータ量が少なくなるようなパラメータを求めていきます。総データ量$\Psi$が最小になるときの分割サイズ$\phi$は式$(3)$の$\Psi$を$\phi$で偏微分することで求めることができます。

\frac{d\Psi(\phi, \omega)}{d\phi} = \frac{\mu\theta\omega}{2}\left( 1 - \theta \phi^{-(\omega+1)} \right) \tag{4}

$d\Psi/d\phi = 0$になる$\phi$は、

\phi = \left( \frac{1}{\theta} \right)^{-\frac{1}{\omega+1}} \tag{5}

になります。値があるということは最小値が存在することを示しています。例えば配列要素数$\theta$、段階数$\omega$をそれぞれ1,000,000, 1段階とすると、$\phi=100$を得ます。これは、配列要素数100万を1段階の分割で総和処理を行うには、分割数を100にすることで最小の総データ量になることを意味します。そして段階数毎に最小値があることが分かります。総データ量が最小になるときの$\omega$は、$\Psi$を$\omega$で偏微分することで求めることができます。
すなわち、

\frac{d\Psi(\phi, \omega)}{d\omega} = -\frac{\theta \log \phi}{\phi^{\omega}} + \phi + 3 \tag{6}

$d\Psi/d\omega = 0$になる$\omega$は、

\omega = \log_{\phi}{\frac{\theta \log \phi}{\phi + 3}} \tag{7}

となり、この$\omega$を使用する場合は小数部分を切り捨てた整数部分を最小値として採用することができます。これにより、例えば式$(7)$へ配列要素数$\theta$、分割サイズ$\phi$をそれぞれ1,000,000, 100分割を代入すると、$\omega = 2.325...$を得ます。少数以下を切り捨てた2が段階数$\omega$になります。これは、配列要素数100万, 分割数100で行うには、2段階で分割することで最小に近い総データ量になることを意味します。もう一つ、$\omega$を得る方法があります。それは式(5)から$\omega$を得る方法です。式(3)の$\Psi(\phi, \omega)$が最小になるときの$\phi$が式(5)になりますので、このときの$\phi$に対応した$\omega$は

\omega = \log_{\phi}\theta-1 \tag{8}

のようになります。
式(5)、式(8)を使用して、$\omega$、$\phi$を導出する場合、両方を同時に導出することができないため、どちらかを先に決定しておく必要があります。そこで、下に示す図5の結果から$\phi=10$として$\omega$を求めて測定を行いました。ライブラリにはこれを採用しています。
式$(3), (5)$から段階数$\omega$が大きくなるほど総データ量$\Psi$は小さくなること、$\omega$が1よりも大きくなると総データ量が最小になる分割サイズ$\phi$の値は変化することが分かりました。さらに総データ量は分割サイズが増加するほど小さくなりますが、分割サイズが1になると従来法と同一になるため、小さくとも2以上の分割サイズが必要です。これらを加味して分割サイズ、段階数を変化させて計算した総データ量を図示してみます。要素数$\theta$は1,000,000に固定しています。要素数100万に対する最適な分割サイズ10は、100万を素因数分解して得られる$2^{6} \times 5^{6}$のそれぞれの底（2, 5）の最小公倍数に当たります。

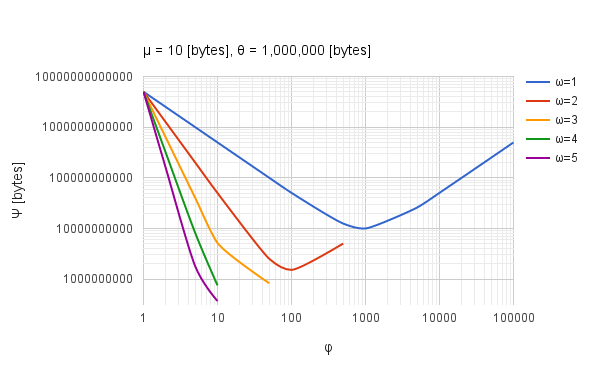
図5. 段階数$\omega$と分割サイズ$\phi$に対する総データ量$\Psi$の関係.

図5は段階数$\omega$と分割サイズ$\phi$に対する総データ量$\Psi$の関係を示した両対数のグラフです。分割サイズが1のとき、すなわち分割していない従来方法の場合は総データ量が最大になっており（図5左上）、分割することが総データ量を小さくする要因になっていることが分かります。また、それぞれの段階で総データ量が最小になる分割サイズがあることも分かります。段階数が大きくなるほど総データ量は小さくなっています。図5から、100万要素数の総和処理には分割サイズ10要素単位で5段階に分けて加算すると最も総データ量が小さくなり、処理時間が最短になるのではないかと推測できます。

ここまでは思考実験として行った流れです。次のセクションで仮説を証明するために思考実験結果に基づいて行った実験結果を記載します。

実験結果

$\hspace{1em}$ 実験結果からはほぼ定量的に言える結果ではあると思われますが、処理時間についての細かい数値はそれぞれの環境の違いやタスク実行時のタイミングなどで異なると思われますのでこれをご了承くださいますと助かります。

Google Apps Scriptへの効果

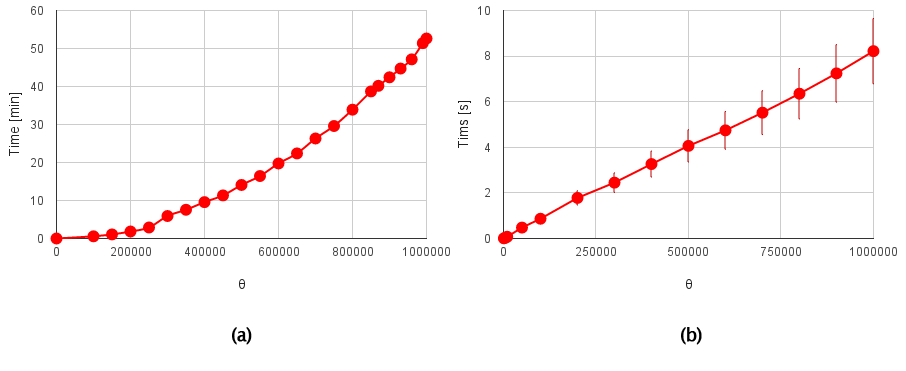
図6. GASを用いた要素数に対する総和処理時間. (a)従来法, (b)ピラミッド方式.

図6 (a), (b)は、それぞれ従来法、ピラミッド方式により総和処理を行った時の要素数$\theta$に対する処理時間を示しています。図6(b)では$\phi=10$として、$\omega$は思考実験で得た結果を使用して各$\theta$で最適化して総データ量$\Psiが最小になるようにしています。図6 (a)は長時間の計算が必要になるため、データ点を増やしてデータ取得回数は1回としています。図6 (b)でのデータ点は10回計算させた場合の平均値を採用し、データ取得時の最小値、最大値からの差に対する割合を全データ点について平均した値をエラーバーとして採用しています。エラーバーが各点で設定していない理由は、Googleスプレッドシートを使用したグラフ作成では各データ点でのエラーバーが一定値あるいは一定の割合で全体に適応することしかできないためです。ただ、実際のデータのエラーバーと比較してもそれほど大きな違いはありません。図6 (a)は図2と同じです。図6 (a), (b)の明らかな違いは、その処理時間です。図6 (a), (b)の縦軸はそれぞれ分、秒です。要素数が100万の場合を比較すると、概要で述べたように従来法では52分程度要する処理がピラミッド方式では8秒程度で終了していることが分かります。さらに、要素数に対する処理時間の変化の仕方を見ると、従来方式では要素数の二乗に比例して処理時間が増加していますが、ピラミッド方式では要素数に対してリニアに処理時間が増加していることが分かります。これは思考実験で議論した、要素数に対する処理中に動く総データ量の関係とよく一致します。すなわち、GASでは総和処理中に動く総データ量は直接処理時間に関係していることが分かります。さらに、総データ量が要素数に対して比例するなら処理時間も比例し、これが処理時間短縮につながるのではないかとの仮説を証明できたと言えます。これにより、GASを用いた配列の全要素（各要素は文字列）の総和処理に対してピラミッド方式は十分有効であると言えます。

結果

• ピラミッド方式は、GASを使用した100万の要素数を持つ配列の全要素を総和処理するための効率的な手法であることが分かりました。

• ピラミッド方式を用いることでGASではこれまで52分程度かかった総和処理を8秒程度で完了できるようになりました。

• GASの場合、総和処理中に動く総データ量は直接処理時間に関係していることが分かりました。これは、総データ量の変化と処理時間の変化の相関が弱くなる場合、処理の実行中に何らかの別処理（最適化）が行われていることを示唆できるのではないかとも考えられます。

この結果がGoogleやGASを利用するユーザにとって少しでもお役に立つことができれば幸いです。

付録

ライブラリ

今回得た結果を使ってGAS用にライブラリを作成しました。本来の目的に対して用いるために自分でも使用する予定で作成しました。不便なところや改善点がありましたらご指摘いただけますと幸いです。ライブラリの仕様は下記の通りです。

• 段階数$\omega$はこの検討で得た結果を用いて最適になるようにスクリプト内で設定しています。

• 分割サイズ$\phi$はそれぞれの桁に分解して処理するようにしているため10と固定しています。（この方が効率が良かった）

• 1000以下はピラミッド方式でも順次足し合わせでも大きな差は認められなかったため従来法で処理します。

使い方は下記の通りです。

SOUWA.souwa(配列, デリミタ, 改行コード);

戻り値として、デリミタ、改行コードが入った文字列を返します。

ライブラリの公開について、これまではプロジェクトキーを公開することになっていましたが、2016年7月12日にProject keyは廃止の方向でScript IDの使用を推奨していましたのでScript IDを公開します。

July 12, 2016

The use of project keys to identify scripts is now deprecated. The preferred unique identifier for a script is the Script ID. There are no plans to turn off or disable the use of project keys; code that uses project keys will continue to work for the foreseeable future.

Script IDは「1yI93fL6G-jJwdYLCXSnbOkluQntDWo6QLARB6dMqObcJd-BYBd6wyasz」です。これをGASのエディタが開いた状態で リソース - ライブラリ の中の「ライブラリを検索」へ入力して検索するとSOUWAライブラリが表示されます。バージョンは最新で問題ありません。ライブラリの共有設定は行いましたが、問題がありましたらご指摘をお願いします。ライブラリ本体のリポジトリはこちらです。

サンプルスクリプト

ライブラリを用いたサンプルとしてGoogleのスプレッドシートからCSVファイルを出力するスクリプトを用意しました。

sample.s

function ss2csv() {
  var ss_file = "sampless"; // csvに変換したいスプレッドシートのファイル名
  var csv_file = "sampless.csv"; // 出力するcsvファイル名
  var sheet = SpreadsheetApp.open(DriveApp.getFilesByName(ss_file).next());
  var data = sheet.getRange('a1').offset(0, 0, sheet.getLastRow(), sheet.getLastColumn()).getValues();
  var csvdata = SOUWA.souwa(data, ',', '\r\n');
  DriveApp.createFile(csv_file, csvdata, MimeType.CSV);
}

サンプルはスタンドアロンスクリプトです。Googleへログインしている状態でDrive上で作成するか、https://script.google.comへアクセスすることでエディタが起動しますのでそこへ入力して実行させます。ライブラリの導入もエディタ上で行います。

スプレッドシートのファイル名を変更してご使用ください。このスクリプトで70万セルをCSVファイルに変換するのに要する時間は12秒程度でした。一方、スプレッドシート上から手動でcsvとして出力すると3秒程度で終了しましたので、内部での変換方法にはスプレッドシートからcsvへ変換するための方法がスクリプトとは異なっているものと推測します。

**そういえば、**サンプルスクリプトを書いているときに気付いたのですが、以前はsetValues, getValuesの上限は250だったように思います。それを失念したままサンプルを作って動作確認していましたがエラーは出ていないようです。ファイルもきちんとできています。いつの間にか上限が変更されていたようです。今他で動かしているスクリプトは250毎に分けて操作していますのでこれを変更するともう少し速度アップが期待できそうです。

実験で使用したスクリプト

測定で使用したスクリプトをこちらにまとめました。

最後に

• 作成したライブラリによってルーチンワークの作業効率が高まりました。

• これまで使い慣れてきた従来方法でも少し工夫をすると処理効率が改善できることに再認識させられたことは自分にとってとても大きな成果です。

• 改善点がありましたらご指摘下さいますと嬉しいです。

• もしもすでにこのような内容をご存知の場合はお教え頂けますと幸いです。自分の考えた方向性が間違っていないことが分かりますのでとても助かります。また、是非参考にさせていただきたいと思います。