目的
FPGA の開発では高位合成ツールというのがあって、C や Python で書いたプログラムをハードウェア記述言語に変換して FPGA 上でハードウェアとして動作させることもできます。それと同様に、いつの日か量子計算機ハードウェアが実用的になった暁には量子回路をなんらかの高レベル言語で記述するのが当たり前になるかもしれません。
DSL を手軽に作るには Prolog はよい言語なので、量子計算の高位合成がどうあるべきか考えるツールとして使えるように Prolog で初歩的な量子計算シミュレータを作成します。
量子計算シミュレーションは粗行列計算で、これだけについて言えば Prolog はあまり適した言語ではないかもしれませんが、量子計算が意図したとおりの結果になるか手軽に見たい、という使い方には問題ないと思います。
ここでは、例として以下のような記述で量子計算ができるようになることを目指します:
% 量子テレポーテーションのテストプログラム
test_teleport :-
% テレポーテーション対象の量子ビットの準備
circuit( [] -> Q0 ; [X ← init, % 新しい量子ビット X を準備
gate_h(X)]), % X にアダマールゲートを適用する
% テレポーテーション
teleport(Q0 -> _Q1 ; X -> _B).
% 量子テレポーテーション回路
%
% 量子ビット X の状態を量子ビット B にテレポートさせる。
% 開始時の量子状態は Q, 終了時の量子状態は Q2。
%
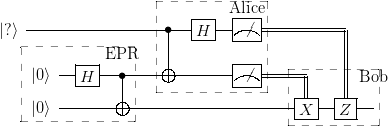
teleport(Q -> Q2 ; X -> B) :-
write('=== initial state ==='), nl,
inspect(Q),
circuit(Q-> Q2 ;
[epr([] -> A, B), % EPR ペアを作る
alice(X, A -> MX, MA), % Alice が測定して結果を送る
bob(B, MX, MA -> B)]), % Bob が情報を受け取る
write('=== final state ==='), nl,
inspect(Q2).
% EPR ペアを作る
%
% エンタングルした2つの量子ビット A, B を返す。
% 開始時の量子状態は Q, 終了時の量子状態は Q2。
%
epr(Q -> Q2 ; [] -> A, B) :-
circuit(Q -> Q2 ;
[[A, B] ← init,
gate_h(A),
gate_cx(A, B)]),
write('=== generated EPR pair ==='), nl,
inspect(Q2).
% Alice
%
% 量子テレポートさせる対象の量子ビット X と、
% エンタングルした2つの量子ビットの片割れ A を元に
% Bob に送る測定結果 MX, MA を返す。
% 開始時の量子状態は Q, 終了時の量子状態は Q2。
%
alice(Q -> Q2 ; X, A -> MX, MA) :-
circuit(Q -> Q2 ;
[gate_cx(X, A),
gate_h(X),
[MX, MA] ← gate_meas([X, A])]),
write('=== Alice observed ==='), nl,
inspect(Q2),
write('MX='), write(MX), nl,
write('MA='), write(MA), nl.
% Bob
%
% Alice から受け取った MX, MA を元に
% 量子ビット B にテレポート元の状態を再現する。
% 開始時の量子状態は Q, 終了時の量子状態は Q2。
%
bob(Q -> Q2 ; B, MX, MA -> B) :-
( MA = 1 -> circuit(Q -> Q1 ; [gate_x(B)]) ; Q = Q1 ),
( MX = 1 -> circuit(Q1 -> Q2 ; [gate_z(B)]) ; Q1 = Q2 ),
write('=== Bob operated ==='), nl,
inspect(Q2).
前に「Prolog で量子計算ができないか検討してみる」と題して数式処理から書き始めたのですが検討レベルで行き詰まってしまったので、他のプログラミング言語で実装経験のある粗行列計算による量子計算シミュレーションをベースとします。
必要なもの
以下があれば基本的な量子計算シミュレーションができます。
- ビット操作
状態ベクトルの操作に必要です。
- 複素数の計算
量子状態の確率振幅の計算に必要です。
- 辞書、ハッシュテーブルなど
状態ベクトルをキーとして複素数を格納できる辞書構造があれば、粗行列を実現できます。
今回は SWI-Prolog の Dicts (名前付きデータ構造) を用いて実装することにしました。
基本的な考え方
量子ビットはそれぞれ ∣0⟩ あるいは ∣1⟩ の状態をとります。
量子ビット数がたかだか 64 程度に制限してよいならば、64bit 符号なし整数で状態ベクトルを表現できます。量子計算機はすべての量子ビットが 0 になるように初期化した状態からスタートするので
100% が、状態 ∣00000..⟩ にある(00000.. は使用する量子ビット分の ∣0⟩ の並び)
というのが初期状態です。位相も初期状態は 0 ということに決めておくと、ここでいう 100% というのは確率振幅 1.0 + 0.0 * i という複素数値で表現できます。状態ベクトルも簡単に二進数で 0 と言い換えることができます。つまり
_{
0 : 1 % ∣0⟩ の確率振幅が 1
}.
('0' をキーとして 1 を保持)というのがこの量子計算機の初期状態です。アダマールゲートを通すとこの状態が2つに分離します。0 番目の量子ビットについてのアダマールゲートだったなら
_{
0 : 0.7071067811865475 % ∣0⟩ の確率振幅は (1.0 + 0.0 * i) / √2
1 : 0.7071067811865475 % ∣1⟩ の確率振幅は (1.0 + 0.0 * i) / √2
}.
になります。これは行列式で書くならば
\frac{1}{\sqrt{2}} \times
\begin{pmatrix}
1 & 1 \\
1 & -1
\end{pmatrix}
という計算を行ったことに対応しています。
さらに 1 番目の量子ビットについてのアダマールゲートに通すと
_{
0 : 0.5 % ∣00⟩ の確率振幅は (1.0 + 0.0i) / 2
1 : 0.5 % ∣10⟩ の確率振幅は (1.0 + 0.0i) / 2
2 : 0.5 % ∣01⟩ の確率振幅は (1.0 + 0.0i) / 2
3 : 0.5 % ∣11⟩ の確率振幅は (1.0 + 0.0i) / 2
}.
と2つの状態が4つに分裂します。このような操作をする行列を任意の n 番目の量子ビットについて書くこうとするとややこしいのですが、実は状態ベクトルの n 番目のビットに着目してそのビットの 0 / 1 に応じて、ビットを反転したりあるいは確率振幅に掛け算をするというだけで実現できます。
複素数の計算
以前書いた複素数計算の記事をモジュール化して再利用できるようにしました。これを複素数計算に用いることにします。
:- use_module(complex, [op(150, xf, '^*'), % 複素数の演算操作
op(180, fx, '√'), % 複素数の演算操作
op(400, yfx, '×'), % 複素数の演算操作
op(400, yfx, '÷'), % 複素数の演算操作
op(500, yfx, '+'), % 複素数の演算操作
op(500, yfx, 'ー'), % 複素数の演算操作
op(900, xfx, '←'), % 複素数の演算操作
'←'/2, % 複素数式の計算
printc/1, % 複素数の表示
printc/2, % 複素数の表示
real_number/2]). % 実数(虚部=:=0)の値を得る
構造体による量子状態の表現
量子状態は、状態ベクトルをキーとして、状態ベクトルの確率振幅値を格納する辞書で表現できます。
これだけでもよいのですが、量子状態を文字列表現するときには最大量子ビット数がいくつなのかを持っていた方が便利です。例えば量子ベクトル∣0⟩ と ∣0000⟩ では前者が量子ビット数 1、後者が量子ビット数 4 ですが、単純に状態ベクトルを二進数の数値で表すとどちらも 0 になって区別が付きません。逆にアトム '0' と '0000' をキーとした辞書にする、という方法もありえますが、これだと計算中に量子ビット数を増やしたくなったときに不便です。
そこで、量子状態は構造体 quantum_states/3 で表現することにし、 quantum_states/3 の第一引数を量子ビット数、第三引数を状態ベクトルと確率振幅値のペアを保持する辞書ということにしました(第二引数については後述するようにデバッグに用います)。
初期状態で無限の数の ∣0⟩ を用意しておいて、必要に応じて使用する量子ビットを割り当てていく、というのが現実なのですが、初期状態はなにもない状態で、量子ビットを作ると∣0⟩ に局在した状態を作って返す、というイメージの以下の述語を用意します。
% 量子ビットが一つも使われていない状態から量子ビットを一つ払い出す
new_qubit([] -> quantum_states(1, _, _{ 0: 1}), qubit(0)) :- !.
% 量子ビットがいくつか払い出された状態で、新たに量子ビットを一つ払い出す
new_qubit(quantum_states(M, B, Q) -> quantum_states(M1, B, Q), Qubit) :-
Qubit = qubit(M),
M1 is M + 1, !.
new_qubit/2 の第一引数は、「量子ビット払い出し前の状態 -> 量子ビット払い出し後の状態」という構造体です。第二引数に作成した量子ビットを「qubit(量子ビットの番号)」という形で返します。
払い出した量子ビットの数を、構造体 quantum_states/3 から得る述語は以下のように書けます:
% 量子ビット数を第二引数に返す
get_max_qubits(quantum_states(M, _, _), M).
粗行列に含まれる量子状態すべてについて処理を繰り返す、というのがここでの計算処理の基本なので、すべての状態ベクトルを取得する述語を定義します:
% 第一引数の量子状態に含まれるすべての状態ベクトルのリストを第二引数に与える
get_all_quantum_states(quantum_states(_, _, Q), States) :-
dict_keys(Q, States), !.
上の述語で得た状態ベクトルに対応する確率振幅値を得る述語です:
get_quantum_amplitude(quantum_states(_, _, Q), State, Amplitude) :-
( Amplitude = Q.get(State) -> true
; Amplitude = 0, ! ).
状態ベクトルとそれに対応する確率振幅値を設定する述語は以下のように書けます。破壊代入ではないので、新しい Dict を作って返す形です:
set_quantum_amplitude(quantum_states(M, _, Q), State, Amplitude -> Q2) :-
Q2 = quantum_states(M, _, Q.put(State, Amplitude)).
上の get/set を組み合わせて確率振幅値を加算する述語が以下です。get_all_quantum_states/2 で得たすべての状態ベクトルについて、そのビット値をチェックして必要に応じて新しい量子状態を add_quantum_amplitude/3 で作り上げる、というのが計算の基本となります。
add_quantum_amplitude(Q, State, Amp -> Q2) :-
( get_quantum_amplitude(Q, State, A0) -> A2 ← A0 + Amp
; A2 = Amp ),
set_quantum_amplitude(Q, State, A2 -> Q2).
add_quantum_amplitude/3 で新しい状態を作るベースとなる、空の状態が必要です。next_quantum_states/2 はそんな空の Dict を作る述語です。
与えられた量子状態と同じ最大量子ビット数を持つ空の量子状態を返します。
next_quantum_states(quantum_states(M, _, _) -> quantum_states(M, _, _{})) :- !.
デバッグのために
誰かが、こんなことを考えたとします。
「ある量子状態 Q0 に、パウリ X ゲート、パウリ Y ゲート、パウリ Z ゲートを適用した結果すべてを見たい」
その結果、以下のように書いてみたとします:
new_qubit([], Q0, Qubit),
gate_x(Q0 -> Qx; Qubit),
gate_y(Q0 -> Qy; Qubit),
gate_z(Q0 -> Qz; Qubit),
これは実はありえない操作です。Q0 は最初の gate_x で破壊されて Qx の状態になっているので、再度別のゲート操作を行うことはできません。
意図的にこのような記述をすることはあまりないかもしれませんが、誤ってこれに近いプログラムを書いてしまう可能性は否定できません。このような操作を禁止するために(そもそもそのような記述ができる文法が良くないのですが)、quantum_states/3 の第二引数はその状態が使用済み (broken) であるかを表すために使っています。未使用なら未定義変数のままで、使用済みなら broken が入っています。
break_quantum_states(quantum_states(_, B, _), Msg) :-
(
var(B)
->
B = broken
;
write('invalid quantum circuit!!!'), write(Msg), fail, !
).
また、デバッグのために与えられた状態を表示する述語を作ります。デバッグのため、というのは本来量子状態は直接観測しえない(観測すると壊れるうえに、観測結果は 0 か 1 かのどちらかでしかない)ためです。
printなんとか、とか writeなんとか、のような名前にせずに inspect/1 という比較的耳慣れない名前を選んだのは「これは実機では使えないものだぞ」と自分に言い聞かせるためです。
inspect(Q) :-
total_probability(Q, P),
N ← √ P,
get_all_quantum_states(Q, States),
inspect(States, Q, N), !.
inspect([], _, _) :- nl, !.
% 確率振幅 0 の項は表示しない
inspect([State|States], Q, N) :-
get_quantum_amplitude(Q, State, Amplitude),
is_amplitude_zero(Amplitude),
!, inspect(States, Q, N).
% 確率振幅が 0 でない項を正規化して表示する
inspect([State|States], Q, N) :-
get_quantum_amplitude(Q, State, Amplitude),
NormalizedAmplitude ← Amplitude / N,
printc(NormalizedAmplitude, with_sign),
write(' * |'), !,
get_max_qubits(Q, MAX_QUBITS),
write_state(0, MAX_QUBITS, State), write('>'), nl, !,
inspect(States, Q, N).
ここで、表示する確率振幅は敢えて元の値そのままではなく全体の確率が 1 になるように正規化しなおした値としています。思ったより数値計算の精度が良くなくて何回か量子ゲートを通すと全体の確率が 1 から微妙にずれて表示が見づらいためです。
% Q 全体の期待値を計算する。計算誤差がなければ P=1 になるはず
total_probability(Q, P) :-
get_all_quantum_states(Q, States),
total_probability(States, Q, 0, P).
total_probability([], _, P, P) :- !.
total_probability([State|States], Q, Ac, P) :-
get_quantum_amplitude(Q, State, A),
Ac2 ← Ac + A * (A^*),
total_probability(States, Q, Ac2, P).
% 与えられた確率振幅 A が 0 なら true
is_amplitude_zero(A) :-
real_number(A, R), (R =:= 0 ; R =:= 0.0 -> true).
% 状態ベクトルを 0 と 1 の並びとして表示する
write_state(MAX_QUBITS, MAX_QUBITS, _) :- !.
write_state(N, MAX_QUBITS, State) :-
( is_one(N, State) -> write(1) ; write(0) ), !,
N1 is N + 1,
write_state(N1, MAX_QUBITS, State).
パウリゲートの実装
パウリ行列に対応するゲート操作です。制御付きゲートで計算を流用したいので gate_x_op / gate_y_op / gate_z_op に行列計算相当の部分を切り出しています。
% パウリ X ゲート
gate_x(Q -> Q2 ; qubit(N)) :-
break_quantum_states(Q, gate_x(qubit(N))),
next_quantum_states(Q -> Q0),
get_all_quantum_states(Q, States), gate_x(States, N, Q, Q0 -> Q2).
% すべての状態について計算を繰り返す
gate_x([], _, _, Q -> Q) :- !.
gate_x([State|States], N, Q, Q0 -> Q2) :-
gate_x_op(State, N, Q, Q0 -> Q1), gate_x(States, N, Q, Q1 -> Q2).
% パウリ Y ゲート
gate_y(Q -> Q2 ; qubit(N)) :-
break_quantum_states(Q, gate_y(qubit(N))),
next_quantum_states(Q -> Q0),
get_all_quantum_states(Q, States), gate_y(States, N, Q, Q0 -> Q2).
% すべての状態について計算を繰り返す
gate_y([], _, _, Q -> Q) :- !.
gate_y([State|States], N, Q, Q0 -> Q2) :-
gate_y_op(State, N, Q, Q0 -> Q1), gate_y(States, N, Q, Q1 -> Q2).
% パウリ Z ゲート
gate_z(Q -> Q2 ; qubit(N)) :-
break_quantum_states(Q, gate_z(qubit(N))),
next_quantum_states(Q -> Q0),
get_all_quantum_states(Q, States), gate_z(States, N, Q, Q0 -> Q2).
% すべての状態について計算を繰り返す
gate_z([], _, _, Q -> Q) :- !.
gate_z([State|States], N, Q, Q0 -> Q2) :-
gate_z_op(State, N, Q, Q0 -> Q1), gate_z(States, N, Q, Q1 -> Q2).
\begin{pmatrix}
0 & 1 \\
1 & 0
\end{pmatrix}
相当の計算は状態ベクトルのビット反転で実現できます。
gate_x_op(State, N, Q, Q0 -> Q1) :-
get_quantum_amplitude(Q, State, A),
( is_amplitude_zero(A) -> Q0 = Q1
; invert_bit(N, State, State2),
add_quantum_amplitude(Q0, State2, A -> Q1)
).
ここで、is_amplitude_zero/1 は、確率振幅値=0 の項を計算結果から削除するために使っています。
\begin{pmatrix}
0 & -i \\
i & 0
\end{pmatrix}
相当の計算は、状態ベクトルのビット反転および当該ビット 0 / 1 に応じて確率振幅値に i あるいは -i を乗算することで実現できます。
gate_y_op(State, N, Q, Q0 -> Q1) :-
get_quantum_amplitude(Q, State, A),
( is_amplitude_zero(A) -> Q0 = Q1
; ( is_zero(N, State) -> A1 ← i * A ; A1 ← -i * A ),
invert_bit(N, State, State2),
add_quantum_amplitude(Q0, State2, A1 -> Q1)).
\begin{pmatrix}
1 & 0 \\
0 & -1
\end{pmatrix}
相当の計算は、当該ビットの 0 / 1 に応じた確率振幅の符号反転によって実現できます。
gate_z_op(State, N, Q, Q0 -> Q1) :-
get_quantum_amplitude(Q, State, A),
( is_amplitude_zero(A) -> Q0 = Q1
; ( is_zero(N, State) -> A1 = A ; A1 ← -A ),
add_quantum_amplitude(Q0, State, A1 -> Q1)).
ここで、状態ベクトルのビット操作のためにユーティリティ述語を作りました:
% 状態ベクトルの N ビット目が 0 なら true
is_zero(N, State) :-
Mask is 1 << N,
Result is State /\ Mask,
Result =:= 0.
% 状態ベクトルの N ビット目が 1 なら true
is_one(N, State) :-
Mask is 1 << N,
Result is State /\ Mask,
Result =:= Mask.
% 状態ベクトルの N ビット目を 0 / 1 反転させる
invert_bit(N, State, State2) :-
Mask is 1 << N,
State2 is State xor Mask.
制御付きパウリゲートの実装
制御ビットの状態によって操作したりしなかったりを制御できるパウリゲートです。
パウリ X ゲート(ノットゲート)と制御付き X ゲート(制御付きノットゲート)があれば古典的な可逆ブール回路が構成できます。
gate_cx(Q -> Q2 ; qubit(C), qubit(N)) :-
break_quantum_states(Q, gate_cx(qubit(C), qubit(N))),
next_quantum_states(Q -> Q0),
get_all_quantum_states(Q, States), gate_cx(States, C, N, Q, Q0 -> Q2).
% すべての状態について計算を繰り返す
gate_cx([], _, _, _, Q -> Q) :- !.
gate_cx([State|States], C, N, Q, Q0 -> Q2) :-
( is_zero(C, State) -> gate_i_op(State, Q, Q0 -> Q1)
; gate_x_op(State, N, Q, Q0 -> Q1) ),
gate_cx(States, C, N, Q, Q1 -> Q2).
gate_cy(Q -> Q2 ; qubit(C), qubit(N)) :-
break_quantum_states(Q, gate_cy(qubit(C), qubit(N))),
next_quantum_states(Q -> Q0),
get_all_quantum_states(Q, States), gate_cy(States, C, N, Q, Q0 -> Q2).
% すべての状態について計算を繰り返す
gate_cy([], _, _, _, Q -> Q) :- !.
gate_cy([State|States], C, N, Q, Q0 -> Q2) :-
( is_zero(C, State) -> gate_i_op(State, Q, Q0 -> Q1)
; gate_y_op(State, N, Q, Q0 -> Q1) ),
gate_cy(States, C, N, Q, Q1 -> Q2).
gate_cz(Q -> Q2; qubit(C), qubit(N)) :-
break_quantum_states(Q, gate_cz(qubit(C), qubit(N))),
next_quantum_states(Q -> Q0),
get_all_quantum_states(Q, States), gate_cz(States, C, N, Q, Q0 -> Q2).
% すべての状態について計算を繰り返す
gate_cz([], _, _, _, Q -> Q) :- !.
gate_cz([State|States], C, N, Q, Q0 -> Q2) :-
( is_zero(C, State) -> gate_i_op(State, Q, Q0 -> Q1)
; gate_z_op(State, N, Q, Q0 -> Q1) ),
gate_cz(States, C, N, Q, Q1 -> Q2).
ここで、単位行列
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix}
に相当する述語として以下を定義しています:
gate_i_op(State, Q, Q0 -> Q1) :-
get_quantum_amplitude(Q, State, A),
add_quantum_amplitude(Q0, State, A -> Q1).
アダマールゲート
\frac{1}{\sqrt{2}} \times
\begin{pmatrix}
1 & 1 \\
1 & -1
\end{pmatrix}
相当の計算です。
gate_h(Q -> Q2 ; qubit(N)) :-
break_quantum_states(Q, gate_h(qubit(N))),
next_quantum_states(Q -> Q0),
get_all_quantum_states(Q, States),
gate_h(States, N, Q, Q0 -> Q2).
gate_h([], _, _, Q -> Q) :- !.
gate_h([State|States], N, Q, Q0 -> Q3) :-
gate_h_op(State, N, Q, Q0 -> Q2),
gate_h(States, N, Q, Q2 -> Q3).
gate_h_op(State, N, Q, Q0 -> Q2) :-
get_quantum_amplitude(Q, State, A),
( is_amplitude_zero(A) -> Q0 = Q2
; (
is_zero(N, State)
->
A0 ← (1 / √2) * A,
A1 = A0,
S0 = State,
invert_bit(N, State, S1)
;
A0 ← (1 / √2) * A,
A1 ← -1 * A0,
S1 = State,
invert_bit(N, State, S0)
),
add_quantum_amplitude(Q0, S0, A0 -> Q1),
add_quantum_amplitude(Q1, S1, A1 -> Q2)
).
その他のゲート
位相回転ゲート、X/Y/Z 軸中心回転操作それぞれのゲートを同様に追加していくことができますが割愛します。
測定操作
量子計算で最も理解し難い操作が測定操作です。指定された量子ビットの観測結果が 1 になる確率を計算して、確率を元に 0 になるか 1 になるかを決めます。0 になるか 1 になるかが決まると同時に量子状態は破壊されて測定結果の 0 あるいは 1 に状態が収縮します。
gate_meas(Q -> Q2 ; qubit(N) -> M) :-
break_quantum_states(Q, gate_meas(qubit(N))),
% 観測結果が 1 になる確率を計算する
measure_probability(Q, N -> P),
% 確率に従って 0 / 1 どちらになるかを決定する
random(0.0, 1.0, R),
( P > R -> M = 1 ; M = 0 ),
% 観測の結果として、状態が収縮する
conditional_copy_quantum_states(Q, N, M -> Q1),
normalize_quantum_states(Q1 -> Q2).
% 与えられた量子ビット N が 1 になる確率を計算する
measure_probability(Q, N -> P) :-
get_all_quantum_states(Q, States),
measure_probability(States, Q, N, 0.0, Sum),
real_number(Sum, P).
measure_probability([], _, _, Sum, Sum) :- !.
measure_probability([State|States], Q, N, Ac, Sum) :-
( is_zero(N, State) -> Ac2 = Ac
; get_quantum_amplitude(Q, State, A),
Ac2 ← Ac + A * (A^*) ),
measure_probability(States, Q, N, Ac2, Sum).
% M が 0 か 1 かに応じて状態をコピーする
conditional_copy_quantum_states(Q, N, M -> Q2) :-
next_quantum_states(Q -> Q0),
get_all_quantum_states(Q, States),
conditional_copy_quantum_states(States, Q, N, M, Q0 -> Q2).
conditional_copy_quantum_states([], _, _, _, Q -> Q) :- !.
conditional_copy_quantum_states([State|States], Q, N, M, Q0 -> Q2) :-
get_quantum_amplitude(Q, State, A),
(
is_zero(N, State)
->
(
M =:= 0 -> set_quantum_amplitude(Q0, State, A -> Q1)
;
Q1 = Q0
)
;
(
M =:= 0 -> Q1 = Q0
;
set_quantum_amplitude(Q0, State, A -> Q1)
)
),
conditional_copy_quantum_states(States, Q, N, M, Q1 -> Q2).
% 全体の期待値が 1 になるように正規化する
normalize_quantum_states(Q -> Q2) :-
total_probability(Q, P),
next_quantum_states(Q -> Q0),
R ← 1 / P,
get_all_quantum_states(Q, States), mult_amplitude(States, Q, R, Q0 -> Q2).
mult_amplitude([], _, _, Q -> Q) :- !.
mult_amplitude([State|States], Q, R, Q0 -> Q2) :-
get_quantum_amplitude(Q, State, A),
A1 ← A * R,
set_quantum_amplitude(Q0, State, A1 -> Q1),
mult_amplitude(States, Q, R, Q1 -> Q2).
ゲート操作を並べて回路にする
ここまでに書いた gate_x(Q -> Q1 ; qubit(N)) のような形式で書き並べても構わないのですが、Q -> Q1 , Q1 -> Q2, Q2 -> Q3,... と量子状態の遷移をすべてのゲート操作について書き並べるのは面倒です。
circuit(Q -> Q1 ; [ ゲート操作... ]) のような形で書くと自動的に状態遷移の部分を付けて実行してくれるようにします。また、量子計算機上での操作として量子ビットの初期化や測定操作も circuit/1 内の操作として実行できるように定義します。
circuit(Q -> Q ; []) :- !.
% Qubit ← init の処理
circuit(Q -> Q2 ; [X ← init|Ops]) :-
!,
( var(X) -> new_qubit(Q -> Q1, X), circuit(Q1 -> Q2 ; Ops)
; X = [] -> circuit( Q -> Q2 ; Ops)
; X = [X1|Xs], var(X1) -> new_qubit(Q -> Q1, X1),
circuit( Q1 -> Q2 ; [Xs ← init| Ops])
).
circuit(Q -> Q2 ; [Ms ← gate_meas(Ts) | Ops]) :-
!,
(
Ts = []
->
Ms = [],
circuit( Q -> Q2 ; Ops)
;
Ts = [T1 | Tr]
->
gate_meas(Q -> Q1 ; T1 -> M),
Ms = [M|Mr],
circuit( Q1 -> Q2 ; [ Mr ← gate_meas(Tr) | Ops])
;
Ts = qubit(_)
->
gate_meas(Q -> Q1 ; Ts -> Ms),
circuit( Q1 -> Q2 ; Ops)
).
circuit(Q -> Q2 ; [Circuit | Ops]) :- !,
Circuit =.. [Pred, Arg1 | RestArg],
Unboxed =.. [Pred, Q -> Q1 ; Arg1 | RestArg],
call(Unboxed),
circuit( Q1 -> Q2 ; Ops).
これでひととおり実装できたはずです。最初に書いた test_telepor/0 を実行してみましょう。
?- test_teleport.
=== initial state ===
+0.7071067811865475 * |0>
+0.7071067811865475 * |1>
=== generated EPR pair ===
+0.5 * |000>
+0.5 * |100>
+0.5 * |011>
+0.5 * |111>
=== Alice observed ===
-0.7071067811865476 * |110>
+0.7071067811865476 * |111>
MX=1
MA=1
=== Bob operated ===
+0.7071067811865476 * |110>
+0.7071067811865476 * |111>
=== final state ===
+0.7071067811865476+0.0i * |110>
+0.7071067811865476+0.0i * |111>
true.
最初の状態は |0> と |1> の均等な重ね合わせで、最後に Bob は |110> と |111> の均等な重ね合わせを得ています。つまり、0 番目(一番左側)の量子ビットの状態が 2 番目(一番右側)の量子ビットの状態に移動しています。
まとめ
Prolog で量子計算シミュレータを作成しました。
新しい文法の DSL を思いつきで試してみたい、というときには Prolog はやはり便利だと思います。例えば、
量子テレポーテーションのプログラムで
alice(Q -> Q2 ; X, A -> MX, MA)
でなく
alice(Q -> Q2 ; X ⊗ A -> MX, MA)
という書き方にしたら全体の印象はどう変わるだろうか
などという試みを実際に動作するプログラムとして簡単に検証することができます。
今回は量子計算回路を書けました、実行できました、というだけの記事ですが、いずれ量子計算回路の高位合成についても真面目に考えてみたいと思います。