はじめに
Simulated Annealing(以下 SA)は、さまざまな分野で利用されている代表的な最適化手法のひとつです。
多くの解説では、ボルツマン分布やエントロピー、冷却スケジュールといった理論的な側面が強調されますが、初めて学ぶ方には少しとっつきにくいこともあるでしょう。
しかしSAの本質はもっとシンプルで、「探索中にどのくらい容易に障壁を越えられるか」 という確率的な性質を理解することにあります。
この記事では、SAの基本的な理念を直感的に整理し、Pythonによるシンプルな実装例を通して、探索の特徴を体感的に理解することを目標とします。
私もまだ学び始めたばかりなので、気軽に読んでもらえたら嬉しいです。
本記事の実装コードは Google Colab こちら からも確認できます。
メトロポリス法と探索の柔軟性
SAは基本的に Metropolis法 に基づいています。
現在の状態のエネルギーを $E_\mathrm{old}$、候補となる次の状態のエネルギーを $E_\mathrm{new}$ とします。
遷移時の受理確率 $P$ は次式で与えられます:
P = \min\left(1,\; \exp\left(-\frac{E_\mathrm{new}-E_\mathrm{old}}{T}\right)\right)
- $E_\mathrm{new} < E_\mathrm{old}$ のとき、指数項は $1$ より大きくなるので $P=1$ となり、常に遷移が受理 されます。
- $E_\mathrm{new} > E_\mathrm{old}$ のとき、$P < 1$ となり、確率的に受理 されます。
このときエネルギー差 $\Delta E = E_\mathrm{new}-E_\mathrm{old}$ が大きいほど $P$ は小さくなります。
この「エネルギー差の大きさに応じて受理確率が変わる」という 連続的な重み付け が重要な点です。
単純に「上がったら拒否」するのではなく、「上がり方に応じて許容」することで、大域的な探索が可能になります。
温度 $T$ はこの許容の“緩さ”を制御するパラメータです。
数式だけでなく、実際にグラフで可視化するとその意味がはっきりと見えてきます。
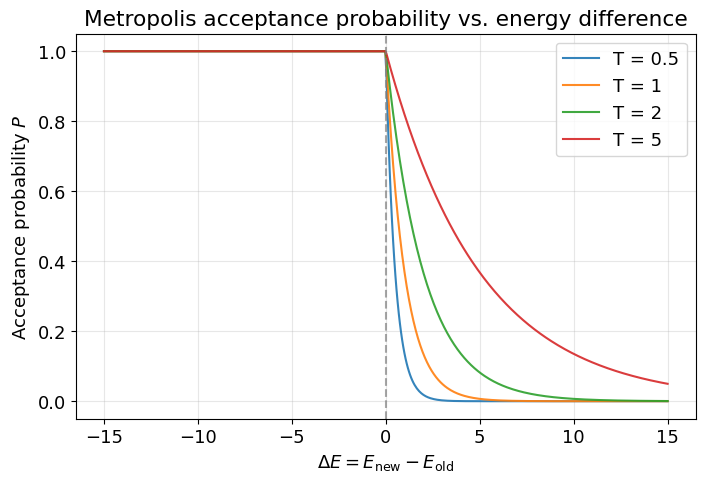
例えば、温度 $T = 0.5, 1, 2, 5$ でプロットすると以下のようになります。
温度が低いと、受理確率は $\Delta E \approx 0$ 付近に集中し、大きい遷移はほとんど拒否されます。その結果、大きな局所解を抜け出すことが難しくなってしまいます。
一方で温度が高すぎると、ほぼランダムに状態を移動するため、最小値付近を丁寧に探索する力が弱まります。
このため、SAでは「広く探索する力」と「局所を掘り下げる力」のバランス が非常に重要になります。
高温からゆっくり冷ますことがポイント
温度は、探索の「動きやすさ」を制御するパラメータです。高温では上り遷移も受け入れやすく、広い領域を探索できます。低温では上り遷移が拒否されやすく、見つけた良い谷の細部を丁寧に掘る挙動へ移ります。
固定温度でメトロポリス法を回すと、理論的にはどんな状態でもいつか踏むこと自体はできると思います。ただし、深い局所谷を越えるにはほぼ天文学的な時間がかかるため、解の捜索として実用的ではありません。
そこで ゆっくり温度を下げる「焼きなまし(annealing)」 という考え方を取り入れます。理論的には
T(t)=\frac{C}{\log(1+t)}
のような十分に遅い冷却スケジュールを用い、かつ $C$ が最小値に至るまでに乗り越えなければならない最大エネルギー障壁よりも大きい場合、
その過程を無限に繰り返すことで、最小値にほぼ確実に収束することが知られています1。
Borel–Cantelli 補題による収束性の理論背景
ここでは、なぜゆっくり冷却すると最小値にたどり着けるのかという理論的な背景を簡潔に説明します。
まず、時刻 $t$ において、最小値に至るために必ず越えなければならない最悪障壁の高さを $d^*$ とします。
この障壁を1 回の遷移で越える確率は
p_t = \exp\left(-\frac{d^*}{T(t)}\right)
で与えられます。
ここで冷却スケジュールを
T(t) = \frac{C}{\log(1+t)}
とすると
p_t = \exp\left(-\frac{d^* \log(1+t)}{C}\right)
= (1+t)^{-\,d^*/C}.
この確率 $p_t$ が時刻 $t$ に依存してどう変化するかが、最小値に収束できるかどうかの分かれ目です。
ここで、Borel–Cantelli 補題を適用するための条件は
\sum_{t=1}^{\infty} p_t = \infty
となるかどうかです。
計算すると、
\frac{d^*}{C} \le 1
\quad\Leftrightarrow\quad
C \ge d^*
のとき、級数は発散します。
Borel–Cantelli 補題の意味するところ
- $C \ge d^*$ のとき → 無限回のチャンス → 確率 1 で障壁を超える
- $C < d^*$ のとき → チャンスが有限 → 超えられない可能性が残る
つまり、チャンスが無限にあればいつか必ず障壁を超えるということです。
これが、理論的に「ゆっくり冷却すれば最小値に収束しやすくなる」とされる背景になっています。
ただ、こうした冷却スケジュールは理論的には有効でも、図のように変化が緩やかすぎて実用的な時間では冷却しきれません。
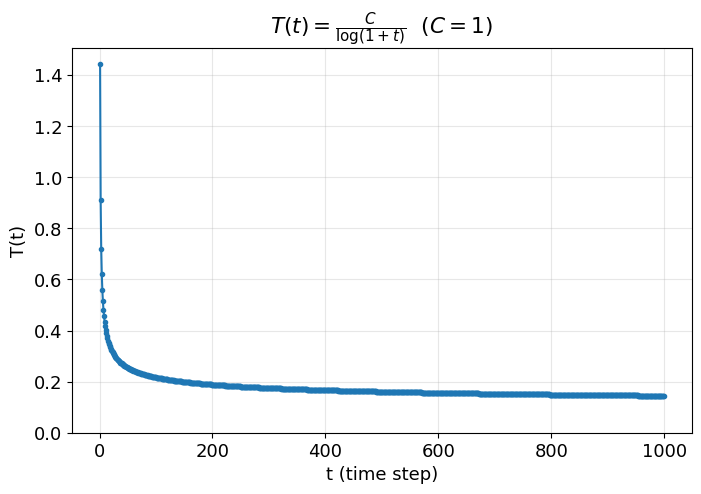
そのため、より計算効率を重視した実用的な温度遷移が使われるのが一般的です。
本記事の実装では、代表例として 指数型の温度スケジュール を用います。
イジングモデルへの適用例
SAの基本的な挙動を具体的に見るために、イジングモデルを題材に Python で解いてみます。ここでは複雑な物理系は扱わず、SAがどのようにエネルギーを下げていくかをシンプルに観察することを目的とします。
イジングモデルの定義
イジングモデルのエネルギー関数は
E(\mathbf{s}) = -\sum_{i<j} J_{ij} s_i s_j - \sum_i h_i s_i
で与えられます。
ここで $s_i \in {-1, +1}$ はスピン変数、$J_{ij}$ はスピン $i$ と $j$ の間の相互作用係数、$h_i$ は外場です。
今回の例では以下のような単純化を行っています:
- 外場はゼロ:$h_i = 0$
- $J_{ij}$ は平均 0、分散 $\sigma^2 = 0.25^2$ の正規分布からランダム生成
- スピン数 $N = 16$
メトロポリス法による遷移
探索中はランダムに1つのスピンを反転し、エネルギー差
\Delta E = E_\mathrm{new} - E_\mathrm{old}
を計算します。
遷移はメトロポリス法に従い、受理確率
P = \min\left(1,\; \exp\left(-\frac{\Delta E}{T}\right)\right)
で行います。
$\Delta E > 0$ でも温度 $T$ が高ければ確率的に受理されるため、局所解を抜けやすくなります。
温度スケジュール
温度 $T$ は探索の広さを制御するパラメータです。
今回は単純な指数型の冷却スケジュール
T(t) = T_0 \left(\frac{T_\mathrm{end}}{T_0}\right)^{\frac{t}{t_\mathrm{max}}}
を用いています。
- $T_0 = 5.0$
- $T_\mathrm{end} = 0.1$
- $t_\mathrm{max} = 3000$ ステップ
初期は高温で大域的に探索し、時間とともに温度を下げて局所探索へ移行します。
実装コード
import numpy as np
import matplotlib.pyplot as plt
import copy
plt.rcParams["font.size"] = 13
# === Brute-force ===
def get_binary_list(num, N):
"""整数をNビットの2進配列に変換"""
return list(map(int, np.binary_repr(num, width=N)))
def brute_force(J, h=None):
"""全探索でIsingモデルの最小エネルギーを求める"""
N = J.shape[0]
if h is None:
h = np.zeros(N)
min_energy = 1e20
for z in range(2**N):
spins = np.array(get_binary_list(z, N))
spins = 2 * (spins > 0) - 1
E = -0.5 * (J @ spins).dot(spins) - h.dot(spins)
if E < min_energy:
min_energy = E
return min_energy
# === Energy function ===
def energy(spins, J, h=None):
if h is None:
h = np.zeros(J.shape[0])
return -0.5 * spins @ J @ spins - h @ spins
# === Simulated Annealing ===
def simulated_annealing(J, h=None, T0=10.0, T_end=0.001, steps=5000, seed=0):
N = J.shape[0]
rng = np.random.default_rng(seed)
spins = rng.choice([-1, 1], size=N)
E = energy(spins, J, h)
best_E = E
E_hist = [E]
T_hist = []
accepted = 0 # ← 受理回数カウント
for step in range(steps):
T = T0 * (T_end / T0) ** (step / steps)
T_hist.append(T)
i = rng.integers(N)
new_spins = spins.copy()
new_spins[i] *= -1
new_E = energy(new_spins, J, h)
dE = new_E - E
# メトロポリス法
if dE < 0 or rng.random() < np.exp(-dE / T):
spins, E = new_spins, new_E
accepted += 1 # ← 受理カウント
if E < best_E:
best_E = E
E_hist.append(E)
accept_ratio = accepted / steps
return best_E, np.array(E_hist), np.array(T_hist), accept_ratio
# === ランダムJ ===
def make_random_J(N, sigma=0.25, seed=0):
rng = np.random.default_rng(seed)
W = rng.normal(0.0, sigma, size=(N, N))
J = (W + W.T) / 2.0
np.fill_diagonal(J, 0)
return J
# === パラメータ設定 ===
N = 16
J = make_random_J(N, sigma=0.25, seed=42)
h = np.zeros(N)
T0 = 5.0
T_end = 0.1
steps = 3000
# === Brute Force ===
E_bf = brute_force(J, h)
print(f"[BF] Ground Energy: {E_bf:.6f}")
# === SA ===
E_sa, E_hist, T_hist, accept_ratio = simulated_annealing(J, h, T0=T0, T_end=T_end, steps=steps)
print(f"[SA] Best Energy: {E_sa:.6f}")
print(f"ΔE = {E_sa - E_bf:.4e}")
print(f"Acceptance ratio: {accept_ratio:.3f}")
# === 可視化 ===
fig, axes = plt.subplots(2, 1, figsize=(8, 6), sharex=True,
gridspec_kw={'height_ratios':[1,1.5]})
plt.subplots_adjust(hspace=0.05)
# --- (1) 温度スケジュール ---
axes[0].plot(T_hist, color="tab:blue", lw=1.5)
axes[0].set_ylabel("Temperature $T$")
axes[0].grid(alpha=0.3)
axes[0].set_title(
f"Simulated Annealing: Temperature and Energy Evolution\n"
f"(Acceptance ratio = {accept_ratio:.2f})"
)
# --- (2) エネルギー履歴 ---
axes[1].plot(E_hist, color="tab:purple", lw=1.5, label="SA Energy")
axes[1].axhline(E_bf, color="tab:orange", ls="--", label="Ground truth (BF)")
axes[1].set_xlabel("Step $t$")
axes[1].set_ylabel("Energy $E$")
axes[1].legend()
axes[1].grid(alpha=0.3)
plt.show()
実行結果
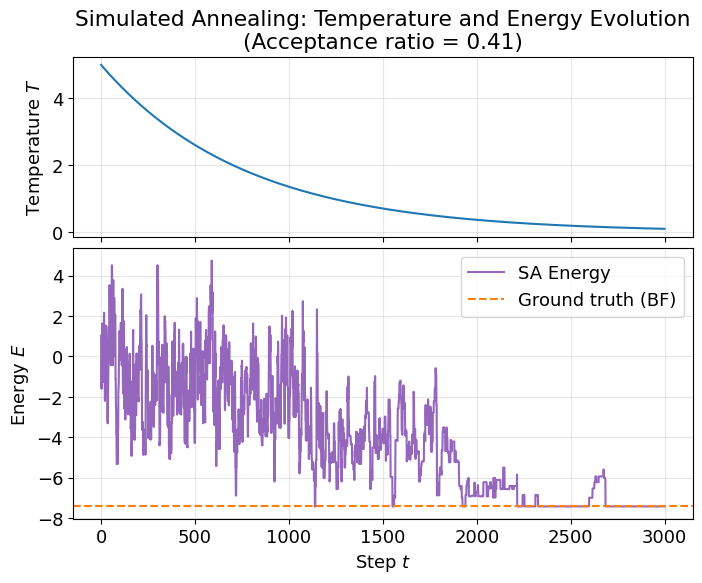
上段のプロットは温度スケジュール、下段はエネルギー履歴を示しています。
SAの結果は、全探索(Brute Force; BF) と同じ最小状態付近の解を見つけられていることがわかります。
受理率と探索の関係
ちなみに、受理率(Acceptance ratio)という指標があるので、ここで簡単に説明します。
今回の値は 0.41 で、全ステップのうち約 40% の遷移が受け入れられたことを意味します。
受理率とは、1 ステップごとの変化(スピン反転)が実際に採用された割合のことです。
つまり「どれくらいの頻度で状態が更新されているか」を表します。
- 受理率はエネルギー差と温度のバランスで決まり、温度が高くても差が大きければ受け入れられにくい
- 差が小さければ、温度が低くても受け入れられる場合もある
このように、受理率は探索の「勢い」や「進み方」の目安になります。
今回は詳しいチューニングには踏み込みませんが、温度スケジュールとエネルギー差の関係を観察すると、探索の挙動がよりクリアに見えてくると思います。
おわりに
本記事では、Simulated Annealing(SA)の基本的な考え方を、理論とPython実装の両面から紹介しました。
SAはシンプルな数式で表される一方で、温度スケジュールとエネルギー差の関係を意識することで、探索のダイナミクスを直感的に理解できます。
最適化には、勾配法のように谷を滑らかに下る手法や、モーメントを導入した手法など、さまざまなアプローチがあります。
その中でもSAは、組合せ最適化の分野で長く使われてきた王道的な方法だと感じています。
そして、SAが「焼きなまし」という物理現象から生まれたように、近年では、CIM(コヒーレントイジングマシン)のように物理そのものを活用して計算を進めるアプローチも提案されています2。
SAを通じて改めて感じたのは、「時間」というパラメータの重要さです。こうした多様な手法が発展してきた背景には、人生という「限られた時間をいかに有効に使うか」という根源的な欲求があるのかもしれません。
言い換えれば、最適化の探究は 私たちの生き方そのものの最適化にも通じているように感じます。