🎯 概要
以下の記事作成後に、修正しました。
https://qiita.com/perorinsub/items/62d19eadf66a2d478df5
この記事では、S&P500の株価データを取得し、Echo State Network (ESN) を用いて予測すしました。
実験
今回は、S&P500の終値を予測します。
- 雑なリザバーで自己回帰
- ハイパーパラメータを最適化し、自己回帰
- 2のモデルに、今日の実際の終値から、明日の終値を予測
1. 雑なリザバーで自己回帰
使用ライブラリ
# 0. ライブラリ読み込みと設定
import numpy as np
from scipy import linalg
import matplotlib.pyplot as plt
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
import pandas as pd
import seaborn as sns
import yfinance as yf
# NumPyの表示設定
np.set_printoptions(precision=4, suppress=True)
1. S&P500データ取得関数
- Yahoo FinanceからS&P500指数(^GSPC)の終値を取得
- データフレームから終値だけを抜き出し、(N,1)のNumPy配列に整形
- サンプル番号の連番tと日付インデックスdatesも返す
- データ取得時に範囲を指定可能(デフォルト: 2010-01-01〜2025-01-01)
# 1. S&P500データ取得関数
def load_sp500_data(start="2010-01-01", end="2025-01-01"):
"""
Yahoo FinanceからS&P500 (^GSPC) の終値を取得して返す。
戻り値:
t : インデックス(日数の連番)
y : (N, 1) の終値ベクトル(NumPy配列)
dates : pandasの日時インデックス(描画用)
"""
df = yf.download("^GSPC", start=start, end=end)
close_prices = df["Close"].values.reshape(-1, 1)
t = np.arange(len(close_prices))
dates = df.index
return t, close_prices, dates
# データ取得
t, data, dates = load_sp500_data()
print("全データ数:", len(data))
2. 学習・テストデータ分割
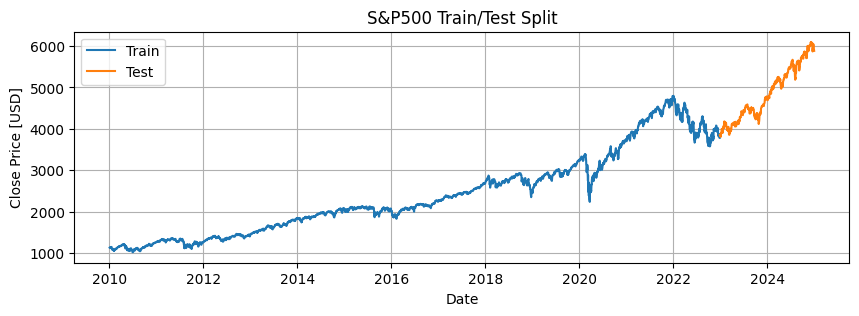
- 最後の2年間(約252日×2)をテストデータとし、それ以前を学習データに分割
- 学習データとテストデータの数を確認
- 時系列データとして学習/テストの分割を可視化して確認
# 2. 学習・テストデータ分割(過去2年をテスト用)
test_years = 2
test_days = 252 * test_years # 営業日換算(概ね252日/年)
train_data = data[:-test_days] # 最後の test_days を除いた部分を学習に使う
test_data = data[-test_days:] # 最後の test_days をテスト(未観測)とする
train_dates = dates[:-test_days]
test_dates = dates[-test_days:]
print(f"学習データ: {len(train_data)}点, テストデータ: {len(test_data)}点")
# 簡単な可視化(学習とテストの分割を確認)
plt.figure(figsize=(10, 3))
plt.plot(train_dates, train_data, label="Train")
plt.plot(test_dates, test_data, label="Test")
plt.title("S&P500 Train/Test Split")
plt.xlabel("Date")
plt.ylabel("Close Price [USD]")
plt.legend()
plt.grid(True)
plt.show()
3. 標準化(学習データ基準)
- 学習データの平均と標準偏差を計算
- 学習データ・テストデータともに、学習データの統計を用いて標準化
- 標準化はESNの安定学習に重要で、情報漏洩防止のためテストデータも学習データ基準で変換
# 3. 標準化(学習データの統計で標準化)
# — 重要: テストデータは学習データの平均・分散で変換する(情報漏洩防止)
data_mean = np.mean(train_data) # 学習データの平均(スカラー)
data_std = np.std(train_data) # 学習データの標準偏差(スカラー)
# (x - mean) / std で各サンプルを標準化する。結果は (N,1) の配列
train_stdized = (train_data - data_mean) / data_std
test_stdized = (test_data - data_mean) / data_std # ← 学習データの平均・分散で変換
print(f"Train mean={data_mean:.2f}, std={data_std:.2f}")
4. 入力重み生成
- 入力層からリザーバへの重みW_inを±scaleのランダム値で初期化
- 0/1の乱数を-1/+1に変換し、スケーリング
- 入力ノード数 × リザーバノード数の形状で作成
# 4. 入力重み生成(入力層 → リザーバ)
def generate_variational_weights(num_pre_nodes, num_post_nodes, scale=0.1):
"""
離散的な ±scale のランダム重みを生成する。
実装:
- まず 0/1 の整数行列を生成(np.random.randint)
- それを 0->-1, 1->+1 に変換(*2-1)
- 最後に scale を掛ける
返却: shape=(num_pre_nodes, num_post_nodes)
用途: 入力値がリザーバ内の各ノードに与える重み(疎にしたい場合はここで工夫)
"""
weights = np.random.randint(0, 2, num_pre_nodes * num_post_nodes)
# reshapeして0/1→-1/+1変換、最後にスケーリング
weights = (weights.reshape(num_pre_nodes, num_post_nodes) * 2 - 1) * scale
return weights
W_in = generate_variational_weights(1, 50)
print("W_in shape:", W_in.shape)
5. リザーバ内部重み生成
- リザーバ内部の重み行列W_resを正規分布で初期化
- 固有値の最大絶対値(スペクトル半径)を計算
- 指定したdesired_spectral_radiusにスケーリング
- スペクトル半径はリザーバの「記憶の長さ」に影響する
# 5. リザーバ内部重み生成(固有値の大きさを制御)
def generate_reservoir_weights(num_nodes, desired_spectral_radius=0.95):
"""
リザーバの内部重み行列を正規分布から生成し、スペクトル半径をdesired_spectral_radiusにスケーリングする。
スペクトル半径(最大の絶対固有値)は、リザーバの「メモリ特性」に強く影響する。
- <1 にすると状態は安定/減衰しやすい(短期記憶)
- 1 に近いと長期の依存を維持しやすい(ただし不安定になりうる)
実装の注意:
- linalg.eigvals は複素固有値を返す可能性があるため絶対値で最大値を取る
- 生成行列を (desired_spectral_radius / spectral_radius) 倍してスケーリングする
返却: shape=(num_nodes, num_nodes)
"""
# 元のランダム行列(平均0、分散1)
weights = np.random.normal(0, 1, (num_nodes, num_nodes))
# 固有値を計算(複素数になる可能性あり)
eigs = linalg.eigvals(weights)
spectral_radius = max(abs(eigs)) # 最大の絶対固有値(正のスカラー)
# 現在のスペクトル半径で割って、目的の半径にスケール
return weights * (desired_spectral_radius / spectral_radius)
W_res = generate_reservoir_weights(50)
print("W_res shape:", W_res.shape)
6. リザーバ状態更新関数
- ESNの状態更新を行う関数
- 式: x(t+1) = (1-α)x(t) + αtanh(W_in^T u(t) + W_res^T x(t))
- 入力と過去状態を線形結合 → 非線形関数(tanh)で更新
- leak_rateで過去状態の減衰率を調整A
# 6. リザーバ状態更新関数
def get_next_reservoir_nodes(input_value, current_state, W_in, W_res,
leak_rate, activator=np.tanh):
"""
ESN(Echo State Network)的な状態更新
数式的には一般に次のように表せる:
x(t+1) = (1 - α) * x(t) + α * f( W_in^T u(t) + W_res^T x(t) )
ここで:
- α : leak_rate(0~1) — 1 に近いほど現在の入力反映が強い(高速応答)
- f : 活性化関数(デフォルト tanh)
- u(t) は入力ベクトル
実装詳細(コードと対応):
u = np.array(input_value).reshape(1, -1)
-> 行ベクトル形式にして W_in と掛け算可能にする
next_state = (1 - leak_rate) * current_state
-> 過去の状態の減衰(リーク項)
next_state += leak_rate * (u @ W_in + current_state @ W_res).ravel()
-> 新しい入力と現在状態からの線形和(この時点で非線形はまだかけない)
return activator(next_state)
-> 最後に非線形を適用してノード出力として返す
注意:
- 著者によっては活性化を加えた後でリークを掛ける(ここではリークを先に掛けてから活性化)
- 次の層(出力重み)はこのactivatorの結果に対して学習される
"""
# 入力を行ベクトルに変換(1 x input_dim)
u = np.array(input_value).reshape(1, -1)
# 過去状態のリーク(1-α)項でスケール
next_state = (1 - leak_rate) * current_state
# 入力と内部状態の線形結合を計算、ravelで1次元に戻す
next_state += leak_rate * (u @ W_in + current_state @ W_res).ravel()
# 非線形変換(tanh 等)をして次の状態を得る
return activator(next_state)
7. 出力重み学習(リッジ回帰)
- 学習したリザーバ状態から出力重みW_outをリッジ回帰で求める
- 正則化付き最小二乗: W_out = (X^T X + λI)^(-1) X^T Y
- λ(ridge_lambda)で過学習を抑制
- 入力X: リザーバの出力状態、出力Y: 次時刻の標準化株価
# 7. 出力重み学習(リッジ回帰)
def update_weights_output(log_reservoir_nodes, targets, ridge_lambda):
"""
リッジ回帰で出力重み W_out を求める。
数式(正則化付き最小二乗):
W_out = (X^T X + λ I)^{-1} X^T Y
ここで:
- X: 入力行列(サンプル数 × 特徴数) → ここでは reservoirs の出力
- Y: 目標出力(サンプル数 × 1)
- λ: リッジ(L2)正則化パラメータ
実装上の注意:
- 正則化行列 reg = λ I を X^T X に足すことで行列の逆の安定化を行う
- N = X.shape[1] (特徴次元)を使って reg を作成
- 行列サイズに注意: inv は (N x N)、X.T は (N x samples)、Y は (samples x 1)
入力形状の整合性:
- ここでは X の行がサンプル、列が特徴(reservoirノード)
- X.T @ X は (features x features)
返却: W_out(shape: features x 1) — reservoir の線形結合係数
"""
X = log_reservoir_nodes
Y = targets
N = X.shape[1] # 特徴(リザーバノード)数
# 正則化行列(特徴数次元の単位行列に lambda を掛ける)
reg = np.eye(N) * ridge_lambda
# 正則化付き正規方程式を解く(逆行列を明示的に取る実装)
inv = np.linalg.inv(X.T @ X + reg)
W_out = inv @ X.T @ Y
return W_out
8. 学習フェーズ
- 学習データを1ステップずつリザーバに入力し、各時刻の内部状態を記録
- ワンステップ先予測の学習用X, Yを準備
- リッジ回帰で出力重みW_outを学習
# 8. 学習フェーズ
leak_rate = 0.2 # リーク率(0~1)
num_nodes = W_res.shape[0] # リザーバノード数(ここでは50)
current_state = np.zeros(num_nodes) # 初期状態はゼロベクトル
log_reservoir_nodes = [] # 学習期間中のリザーバ状態を記録するリスト
# 逐次的に学習データをリザーバに流し、各時刻の内部状態を記録する
for u in train_stdized:
# u は shape (1,1) 相当(各日付の標準化された終値)
current_state = get_next_reservoir_nodes(u, current_state, W_in, W_res, leak_rate)
log_reservoir_nodes.append(current_state)
# リストをNumPy配列に(shape: samples × num_nodes)
log_reservoir_nodes = np.array(log_reservoir_nodes)
# 学習用 X, Y を用意(ワンステップ先予測を学習)
X_train = log_reservoir_nodes[:-1] # t=0..T-2 の内部状態を説明変数に
Y_train = train_stdized[1:] # t=1..T-1 の(標準化した)実際の値を目的変数に
# W_out を学習(リッジ回帰)
W_out = update_weights_output(X_train, Y_train, ridge_lambda=0.01)
9. 予測関数(自己回帰)
- 学習終了時の状態を初期状態として、テスト期間を予測
- 前時刻の予測値を入力としてリザーバ状態を更新
- リザーバ出力に線形結合(W_out)を適用して次の予測を生成
- 長期予測では誤差が累積する可能性あり
# 9. 予測フェーズ(テスト期間を自己回帰で予測)
def predict(initial_input, initial_state, W_in, W_res, W_out,
leak_rate, activator=np.tanh, length_of_sequence=100):
"""
自己回帰方式で未来を予測する関数。
流れ:
- predicted_outputs に直近の入力(標準化済み)を入れる(初期値)
- ループで次のリザーバ状態を計算(前の予測を入力として使用)
- リザーバ状態に線形重み W_out を掛けて次の出力を得る
- その出力を次のステップの入力として使用(自己回帰)
返却: 予測列(length_of_sequence × 1)
注意点:
- 予測は学習時に見た分布(学習データの mean/std)に強く依存する
- 長い予測だと誤差が蓄積しやすい(ロバスト性が低下)
"""
predicted_outputs = [initial_input] # リストの各要素は「標準化済み scalar(1x1)」の想定
reservoir_state = initial_state.copy() # 学習終了時のリザーバ状態をスタートに使う
for _ in range(length_of_sequence):
# 1) リザーバ状態を更新(最後の予測を入力として)
reservoir_state = get_next_reservoir_nodes(predicted_outputs[-1],
reservoir_state, W_in, W_res, leak_rate, activator)
# 2) 出力を線形結合で計算(reservoir_state は 1D array)
next_output = reservoir_state @ W_out
# next_output は (1,) あるいは (1,1) の形になるのでそのままリストに追加
predicted_outputs.append(next_output)
# 最初の初期入力は予測列に含めていないため [1:] で切る
return np.array(predicted_outputs[1:]).reshape(-1, 1)
# 学習の最終入力・最終状態からテスト期間分を予測(標準化データで動く)
initial_input = train_stdized[-1] # 学習データの最後の標準化値(次の時刻を予測するための開始点)
initial_state = log_reservoir_nodes[-1] # 学習で得た最後のリザーバ状態(初期状態)
predicted_std = predict(
initial_input=initial_input,
initial_state=initial_state,
W_in=W_in,
W_res=W_res,
W_out=W_out,
leak_rate=leak_rate,
length_of_sequence=len(test_stdized) # テスト期間と同じ長さだけ予測
)
10. 標準化逆変換 & 精度評価
- 標準化値を元の株価スケールに戻す
- RMSE, MAE, R²で予測精度を評価
- 標準化スケールと実スケールの両方で評価
# 10. 標準化を逆変換(実際の価格スケールに戻す)
predicted = predicted_std * data_std + data_mean
# 10.5. 予測精度評価(実スケール & 標準化スケールの両方)
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
# --- 実スケール(USD単位) ---
rmse_usd = np.sqrt(mean_squared_error(test_data, predicted))
mae_usd = mean_absolute_error(test_data, predicted)
r2_usd = r2_score(test_data, predicted)
# --- 標準化スケール(単位なし) ---
rmse_std = np.sqrt(mean_squared_error(test_stdized, predicted_std))
mae_std = mean_absolute_error(test_stdized, predicted_std)
r2_std = r2_score(test_stdized, predicted_std)
print("\n=== Evaluation on Test Data ===")
print("【実スケール(USD)】")
print(f"RMSE : {rmse_usd:.4f} USD")
print(f"MAE : {mae_usd:.4f} USD")
print(f"R² : {r2_usd:.4f}")
print("\n【標準化スケール】")
print(f"RMSE : {rmse_std:.4f}")
print(f"MAE : {mae_std:.4f}")
print(f"R² : {r2_std:.4f}")
=== Evaluation on Test Data ===
【実スケール(USD)】
RMSE : 1474.1640 USD
MAE : 1282.6757 USD
R² : -4.1266
【標準化スケール】
RMSE : 1.4914
MAE : 1.2977
R² : -4.1266
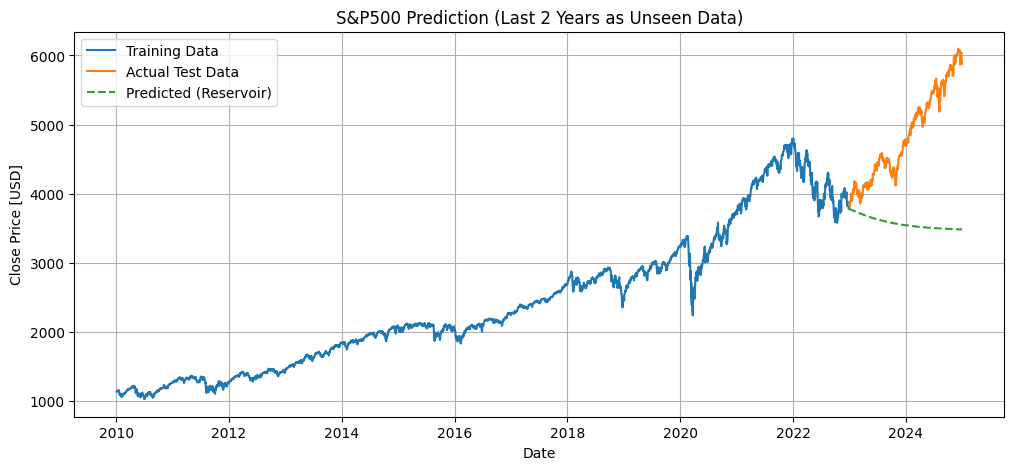
11. 結果可視化
- 学習データ、テストデータ、予測結果を1つのグラフにプロット
- 視覚的に予測の精度を確認
- テスト期間の予測が学習データからどの程度乖離しているかを確認
# 11. 結果可視化
plt.figure(figsize=(12, 5))
plt.plot(train_dates, train_data, label="Training Data")
plt.plot(test_dates, test_data, label="Actual Test Data")
plt.plot(test_dates, predicted, label="Predicted (Reservoir)", linestyle='--')
plt.title("S&P500 Prediction (Last 2 Years as Unseen Data)")
plt.xlabel("Date")
plt.ylabel("Close Price [USD]")
plt.legend()
plt.grid(True)
plt.show()
# 結果概要
print("Predicted shape:", predicted.shape)
print("First 5 predicted values:\n", predicted[:5])
2. ハイパーパラメータを最適化し、自己回帰
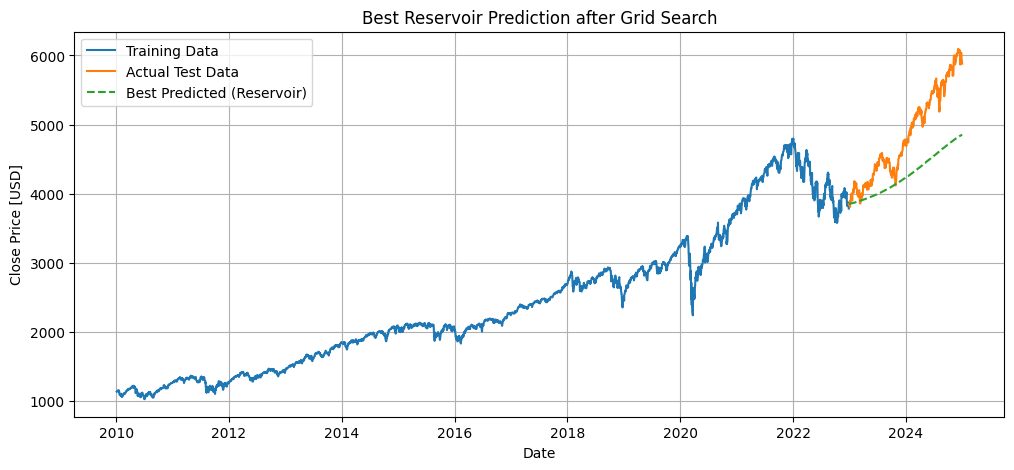
12. グリッドサーチで最適化
- リザーバノード数、リーク率、スペクトル半径、リッジ正則化係数のハイパーパラメータを全探索
- 各組み合わせで学習・予測を行い、RMSEを評価
- 最良RMSEのパラメータと予測結果を保持
- 最適モデルで再度予測し、グラフに可視化
# 12. グリッドサーチ
# 調整するハイパーパラメータの範囲を設定
param_grid = {
"num_nodes": [10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 150], # リザーバのノード数
"leak_rate": [0.1, 0.2, 0.3, 0.4, 0.5], # リーク率
"spectral_radius": [0.5, 0.6, 0.7, 0.8, 0.9, 1.0], # リザーバ内部重みのスペクトル半径
"ridge_lambda": [0.001, 0.01, 0.1] # 出力重みリッジ回帰の正則化係数
}
results = [] # 全組み合わせの結果を保存
best_rmse = np.inf # 最良RMSEを初期化
best_params = None # 最良パラメータ
best_predicted_std = None # 最良モデルの予測結果
print("=== Grid Search Start ===")
# 各ハイパーパラメータの全組み合わせをループ
for num_nodes in param_grid["num_nodes"]:
for leak_rate in param_grid["leak_rate"]:
for spectral_radius in param_grid["spectral_radius"]:
for ridge_lambda in param_grid["ridge_lambda"]:
# 1. 重み初期化
W_in = generate_variational_weights(1, num_nodes) # 入力重み
W_res = generate_reservoir_weights(num_nodes, spectral_radius) # リザーバ重み
current_state = np.zeros(num_nodes) # リザーバ状態初期化
log_reservoir_nodes = [] # 各時刻のリザーバ状態を保存
# 2. 学習フェーズ
for u in train_stdized:
# リザーバ状態を1ステップ更新
current_state = get_next_reservoir_nodes(u, current_state, W_in, W_res, leak_rate)
log_reservoir_nodes.append(current_state)
log_reservoir_nodes = np.array(log_reservoir_nodes)
X_train = log_reservoir_nodes[:-1] # 入力(1ステップ前のリザーバ状態)
Y_train = train_stdized[1:] # 目標出力(標準化済み次時刻データ)
# 3. 出力重みをリッジ回帰で学習
W_out = update_weights_output(X_train, Y_train, ridge_lambda)
# 4. 予測フェーズ
initial_input = train_stdized[-1] # 学習最後の値を初期入力
initial_state = log_reservoir_nodes[-1] # 学習最後のリザーバ状態
predicted_std = predict(
initial_input=initial_input,
initial_state=initial_state,
W_in=W_in,
W_res=W_res,
W_out=W_out,
leak_rate=leak_rate,
length_of_sequence=len(test_stdized) # テスト期間の長さ
)
# 5. 評価
# 標準化データでのRMSEを計算
rmse_std = np.sqrt(mean_squared_error(test_stdized, predicted_std))
# 結果をリストに保存
results.append({
"num_nodes": num_nodes,
"leak_rate": leak_rate,
"spectral_radius": spectral_radius,
"ridge_lambda": ridge_lambda,
"rmse_std": rmse_std
})
# 6. 最良モデルの更新
if rmse_std < best_rmse:
best_rmse = rmse_std
best_params = {
"num_nodes": num_nodes,
"leak_rate": leak_rate,
"spectral_radius": spectral_radius,
"ridge_lambda": ridge_lambda
}
best_predicted_std = predicted_std
# 現在の組み合わせとRMSEを表示
print(f"nodes={num_nodes:3d}, leak={leak_rate:.2f}, ρ={spectral_radius:.2f}, λ={ridge_lambda:.3f} -> RMSE={rmse_std:.5f}")
print("\n=== Grid Search Done ===")
print("Best Params:", best_params)
print(f"Best RMSE (standardized): {best_rmse:.5f}")
# 7. 最良モデルの実スケール予測
predicted = best_predicted_std * data_std + data_mean
# 8. プロット作成
plt.figure(figsize=(12, 5))
plt.plot(train_dates, train_data, label="Training Data")
plt.plot(test_dates, test_data, label="Actual Test Data")
plt.plot(test_dates, predicted, "--", label="Best Predicted (Reservoir)")
plt.title("Best Reservoir Prediction after Grid Search")
plt.xlabel("Date")
plt.ylabel("Close Price [USD]")
plt.legend()
plt.grid(True)
plt.show()
Best Params: {'num_nodes': 10, 'leak_rate': 0.1, 'spectral_radius': 0.5, 'ridge_lambda': 0.01}
Best RMSE (standardized): 0.68363
3. 2のモデルに、今日の実際の終値から、明日の終値を予測
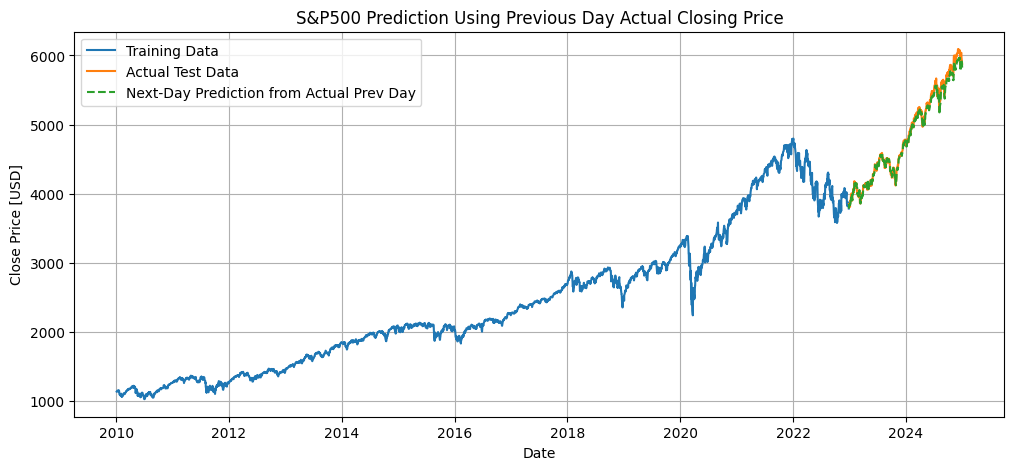
13. 前日実値から翌日予測と精度評価
- 学習済みのESNモデルを使用し、前日の実際終値から翌日の終値を逐次予測
- テスト期間全体をループで処理し、各日の予測値を記録
- 標準化を逆変換して実際の株価スケールに戻す
- 学習データ・テストデータ・予測値を同じグラフに描画
- 精度評価として、RMSE, MAE, R² を標準化スケールと実スケールの両方で算出
# --- 前日実値から翌日予測(テスト期間全体) ---
pred_next_day_std = []
res_state = log_reservoir_nodes[-1] # 学習終了時の最後のリザーバ状態
prev_day_actual_std = train_stdized[-1] # 初日の前日は学習データ最後の値
for actual_std in test_stdized:
# 前日の実値から翌日を予測
next_pred_std, res_state = predict_next_day(prev_day_actual_std, res_state,
W_in, W_res, W_out, leak_rate)
pred_next_day_std.append(next_pred_std)
# 次のステップは実際の値を入力
prev_day_actual_std = actual_std
# 配列化 & 標準化逆変換
pred_next_day_std = np.array(pred_next_day_std).reshape(-1, 1)
pred_next_day = pred_next_day_std * data_std + data_mean
# --- プロット作成(既存グラフ形式に合わせる) ---
plt.figure(figsize=(12, 5))
plt.plot(train_dates, train_data, label="Training Data") # 学習データ
plt.plot(test_dates, test_data, label="Actual Test Data") # テストデータ
plt.plot(test_dates, pred_next_day, "--", label="Next-Day Prediction from Actual Prev Day") # 破線で予測
plt.title("S&P500 Prediction Using Previous Day Actual Closing Price")
plt.xlabel("Date")
plt.ylabel("Close Price [USD]")
plt.legend()
plt.grid(True)
plt.show()
# --- 精度評価 ---
# 標準化スケール
rmse_std_next = np.sqrt(mean_squared_error(test_stdized, pred_next_day_std))
mae_std_next = mean_absolute_error(test_stdized, pred_next_day_std)
r2_std_next = r2_score(test_stdized, pred_next_day_std)
# 実スケール(USD)
rmse_usd_next = np.sqrt(mean_squared_error(test_data, pred_next_day))
mae_usd_next = mean_absolute_error(test_data, pred_next_day)
r2_usd_next = r2_score(test_data, pred_next_day)
print("\n=== Next-Day Prediction Evaluation (Using Previous Actual Close) ===")
print("【実スケール(USD)】")
print(f"RMSE : {rmse_usd_next:.4f} USD")
print(f"MAE : {mae_usd_next:.4f} USD")
print(f"R² : {r2_usd_next:.4f}")
print("\n【標準化スケール】")
print(f"RMSE : {rmse_std_next:.4f}")
print(f"MAE : {mae_std_next:.4f}")
print(f"R² : {r2_std_next:.4f}")
=== Next-Day Prediction Evaluation (Using Previous Actual Close) ===
【実スケール(USD)】
RMSE : 58.9503 USD
MAE : 46.5036 USD
R² : 0.9918
【標準化スケール】
RMSE : 0.0596
MAE : 0.0470
R² : 0.9918
結果
- 最初に、適当なパラメーターで自己回帰的に予測を試みましたが、全く一致せず、精度はほとんど得られませんでした。
- 次に、ハイパーパラメーターをある程度探索して調整することで精度は向上しましたが、実用レベルには達しませんでした。
- 最後に、前日の実際の終値を逐次的に入力する方法では、ある程度使える精度が得られました。株価のように実際の値をリアルタイムで取得でき、予測に猶予がある場合には、この方法が現実的だと感じます(もちろん、他のモデルでも同様のことは可能です)。