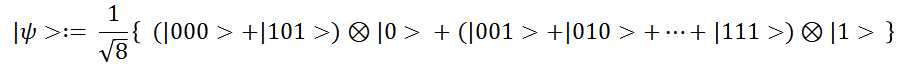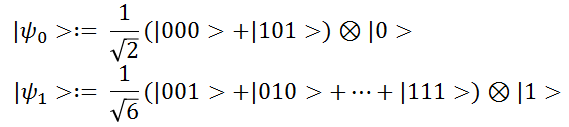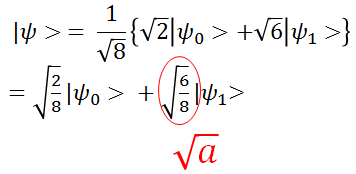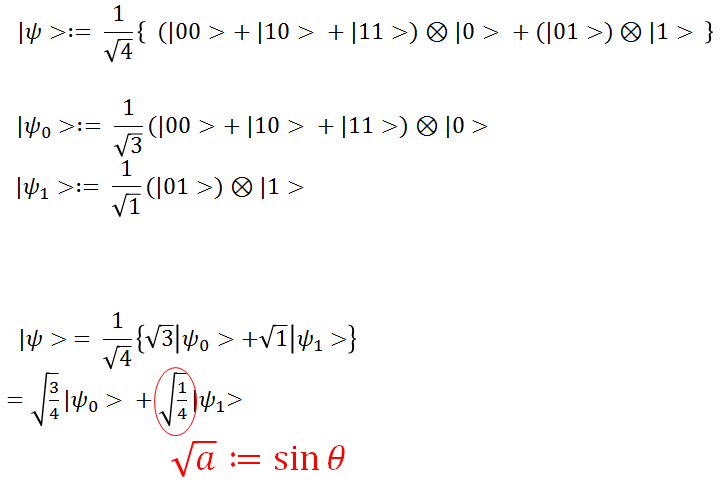Practical numerical integration on NISQ devices
以下の論文
Practical numerical integration on NISQ devices
を確認してみます。
論文中ではCanonical QAE (古典的なQAE)とML-QAEが比較されていますが、今回はCanonical QAEを扱います。
数値積分の量子アルゴリズム
ここで紹介する「積分の量子状態埋め込み」の方法は、あくまで一例(上記論文の方法)で、他にもいろいろな方法があります。
ただ、積分値を振幅に埋め込んで、振幅推定で出すという流れは変わりません。
さて、単位区間$[0,1]$上の1変数関数$f(x)$の積分を求めたいとします。

積分とは$x$軸と$f(x)$で囲まれる部分(緑色部分)の面積に等しいです。
いま、緑色部分を含む1辺1の正方形上に、ランダムに点を打ちます。例えば、8個打ちます。

そして、緑色部分に入ったものを"hit"とみなします。この例では6個の点が"hit"しました。
積分とは$x$軸と$f(x)$で囲まれる部分(緑色部分)の面積に等しい
という事実から、ランダムに打った点が"hit"する割合は積分値に一致するはずです。
積分値を$a$、打った点の数を$N$,hitした点の数を$N_{hit}$とすると、

と計算できます。
この古典的なアイデアをベースに、$N_{hit}/N$を効率的に計算する量子アルゴリズムを考えます。
補助量子ビットを1つ持ってきて、ヒルベルト空間を2つに割ります。

そして、点がhitであったかどうかに応じて、点を”仕分け”していきます。ここで点を量子状態に対応させています。1

ここで、各点に2進数で名前をつけました。点は全部で8個あったので、ラベルは3量子ビットで足りることになります。
仕分けされた量子状態は、
このように書けます。
ここで以下のようなベクトルを定義します。(それぞれ、補助量子ビットが 0 , 1 であるベクトルを意味しています)
すると、仕分けされた量子状態$|\psi \rangle$は、これらの和であって、
このように書けます。
$|\psi_{1} \rangle$の振幅が、求めたい積分値$a$(の平方根$\sqrt{a}$)になっていることがわかります。
この振幅をQAEアルゴリズムで推定すると、古典的な方法の平方根のオラクルコール回数2で計算が終わります。(量子加速)
具体例
$N=4$として、$N_{hit}=1$であったとします。先程と同様に、
となります。 $a=1/4=0.25$です。
ここで$\sqrt{a}=\sin\theta$とおいて、$\theta$の推定に帰着させることが多いです。
これは、QAEの内部で動くQPEアルゴリズムが”位相を推定する”アルゴリズムであり、このほうが見やすいからです。
QAEを用いた$a$の推定については、以下の記事にまとめています。
上記記事の通りにやると、$a = 0.1464466 ≒ 0.25$ という答えが出てきます。ある精度での推定に成功しています。
推定精度を上げるには、QAE内部のQPEで使う補助量子ビット数を増やせばよいです。(上記は3量子ビット使った場合の結果です)
例えば補助量子ビットを7個ぐらい使うと、0.24 ぐらいにはなるようでした。
補助量子ビットを節約したい場合は、Iterative QAE などの方法があります。
こちらもqiskit.aquaに入っていますので、同様の手順で試せます。3
結論
論文を読んで、量子回路の実装から動作確認まで出来た。