自動微分に再入門する(2) #Python3

概要

この記事は自動微分に再入門する(1)の続きです。

今回はPython(PyTorch)で自動微分を実際に使ってみます。

なお、本記事はPyTorchのチュートリアルを参考にしていますのでそちら参照しながら読み進めてください。

関数のフィッティング

データから関数のフィッティングを考えます。データは$\sin(x)$から生成します。

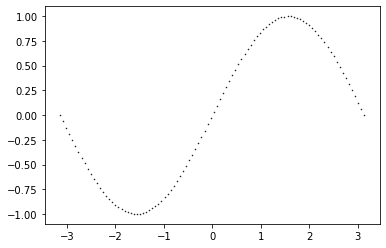
具体的には$[-\pi, \pi]$の範囲で$\sin (x)$の値を等間隔で2000個計算したものがデータとして与えられているとします。

散布図にするとこんな感じです。¹

あくまでも2000個のデータが与えられているだけで$\sin(x)$から計算されたものであることは知らないことにします。その状態で上の散布図をみるとデータを3次関数でフィッティングすればそれなりの結果が得られそうです²

つまり、データから次のパラメータ$a, b, c, d$を推定すればよいということになります。

$$
y_{pred} = a x^3 + b x^2 + c x + d
$$

推定手順

たった4つのパラメータですが、総当たりで値を代入していってそれぞれのモデルを比べるといった方法は全く現実的ではありませんよね。深層学習の場合はパラメータの数が億を超えることもめずらしくないのでなおさらです。

そこで損失関数というものを定義してこれを最小にするようなパラメータの値を推定値にするといった方法が考えられます。今回の問題の場合は最小二乗法を使うことで解析的に解を求めることが可能³ですが、ここでは勾配降下法のアルゴリズムを使います。

具体的には次のようなSTEPをとります。対応するチュートリアルのソースコードを掲載しています。

STEP1

$a, b, c, d$にランダムな値を設定する

a = torch.randn((), device=device, dtype=dtype, requires_grad=True)
b = torch.randn((), device=device, dtype=dtype, requires_grad=True)
c = torch.randn((), device=device, dtype=dtype, requires_grad=True)
d = torch.randn((), device=device, dtype=dtype, requires_grad=True)

STEP2

損失関数$loss$として各$x$で計算した$y, y_{pred}$の差の2乗和を定義する

$$
loss(a, b, c, d) = \sum_{i=1}^{2000} \left(a x_i^3 + b x_i^2 + c x_i + d - y_i \right)^2
$$

loss = (y_pred - y).pow(2).sum()

STEP3

各パラメータ$a, b, c, d$の微分を計算してデータ$x, y$および$a, b, c, d$の値を代入して下記のように各パラメータ$a, b, c, d$の値を更新。

$$
a_{new} = a - r \dfrac{\partial loss}{\partial a}(a, b, c, d)
$$

$$
b_{new} = b - r \dfrac{\partial loss}{\partial b}(a, b, c, d)
$$

$$
c_{new} = c - r \dfrac{\partial loss}{\partial c}(a, b, c, d)
$$

$$
d_{new} = d - r \dfrac{\partial loss}{\partial d}(a, b, c, d)
$$
ただし、$r$は定数

STEP2に戻る

loss.backward()

with torch.no_grad():
    a -= learning_rate * a.grad
    b -= learning_rate * b.grad
    c -= learning_rate * c.grad
    d -= learning_rate * d.grad

自動微分の説明

今回の例だとSTEP3で損失関数を微分する必要がありますのでここで自動微分を使っています。前回出てきたトップダウン型自動微分を使うにはPyTorchの場合backward()を使います。微分結果はa.gradに保持されているのですが、これは各パラメータ$a, b, c, d$の乱数を発生させるときにrequires_grad=Trueをオプションで指定しているからです。

細かい話は色々あるかと思いますが、簡単に自動微分ができるのはすごいなと思いました。

推定結果(おまけ)

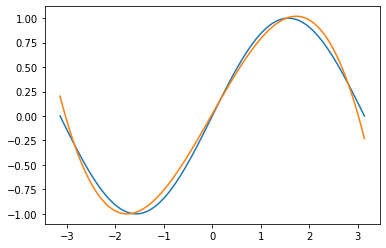
私の環境で実施した推定結果は次のようになりました

$$
y_{pred} = -0.09491576999425888 x^3 + -0.0034224647097289562 x^2 + 0.8678866028785706 x + 0.01983845978975296
$$

ちなみに$\sin(x)$をマクローリン展開⁴すれば次のようになります。

$$
\sin(x) = x - \frac{1}{3!}x^3+ \omicron(x^3)
$$

推定結果と見比べると$x$の係数が1に近い値になっていたり、定数項や$x^2$の係数が0に近いのでそれなりな感じがしますね。

参考文献

実際にはデータ数は2000個なのでmatplotlibでプロットすると線になってしまい散布図っぽくないので数を減らしています。 ↩
俺には$\sin(x)$が見えるぞというツッコミはもっともですが、そういう設定で進めさせてください笑 ↩
$X$に逆行列が存在する場合の計算式としては次式ですが、np.polyfit(x, y, 3)を使えば簡単に求められます。
$$
\hat{\theta} = \left(X^TX\right)^{-1}X^Ty
$$ ↩
マクローリン展開: 関数$f(x)$が0を含めむある区間において$n$回微分可能であるとき
$$
f(x) = f(0) + f'(0)x + \dfrac{f''(0)}{2!}x^2 + \cdots + \dfrac{f^{(n-1)}(0)}{(n-1)!}x^{n-1} + \dfrac{f^{n}(c)}{n!}x^{n}
$$
となる$c\left(0<c<x\right)$が存在する。 ↩