LoginSignup
6
5

More than 5 years have passed since last update.

@mono_shoo

レーベンシュタイン距離とパスを使った配列と同期した別データの更新

Last updated at Posted at 2017-07-17

レーベンシュタイン距離とは？

Wikipedia
Phobos levenshteinDistance
Phobos levenshteinDistanceAndPath ←今回使うのはコレ

詳細は上記ページを見てもらうとして、ざっくり説明すると、編集前の配列Aを編集後の配列Bにするために、「挿入」「変更」「削除」の操作で最も効率よく編集するためにはどうしたら良いか(これがPath)？何回操作が必要か(これがDistance)？を求め、差分・変更点を抽出します。
なお、今回はしれっとD言語を使っていますが、レーベンシュタイン距離とパスが求められるなら、プログラミング言語には依存しない内容だと思います。

どんなときに使うのか？

例1) diff

テキストの変更点を抽出する diff なんかがコレを使った例ですね。

---
 std/algorithm/comparison.d | 103 ++++++++++++++++-----------------------------
 1 file changed, 36 insertions(+), 67 deletions(-)

diff --git a/std/algorithm/comparison.d b/std/algorithm/comparison.d
index e4a8c86c77..0077488261 100644
--- a/std/algorithm/comparison.d
+++ b/std/algorithm/comparison.d
@@ -500,7 +500,7 @@ Params:

 Returns:
     Returns $(D val), if it is between $(D lower) and $(D upper).
-    Otherwise returns the nearest of the two. 
+    Otherwise returns the nearest of the two.

 */
 auto clamp(T1, T2, T3)(T1 val, T2 lower, T3 upper)
@@ -708,14 +708,14 @@ template equal(alias pred = "a == b")
     /++
     This function compares to ranges for equality. The ranges may have
     different element types, as long as $(D pred(a, b)) evaluates to $(D bool)
-    for $(D a) in $(D r1) and $(D b) in $(D r2). 
+    for $(D a) in $(D r1) and $(D b) in $(D r2).
     Performs $(BIGOH min(r1.length, r2.length)) evaluations of $(D pred).
:
:
:

引用元

この例では「変更」を「削除」して「挿入」に置き換えているようですね。
先頭行に「+」が付いている行が「挿入」された行で、先頭行に「-」が付いている行が「削除」された行になっています。

これが代表的な例ではありますが、まだまだ他にも色々と利用できる場面があります。
特に、タイトルで示しているような、配列と同期して、別のデータを更新する場合は有用です。

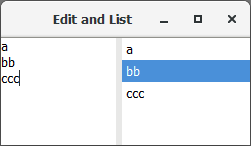
例2) GUIのリストボックス

プログラム内の文字列の配列を表示しているGUI画面のリストボックスがあるとして、その文字列の配列はプログラムの実行中にちょいちょい書き換わり、リストボックスの中身もそれに同期して更新したい…みたいな場合にも有効です。

EditAndList.png

上記の図で、左のテキストボックスの中身を行ごとに分けて string[] 型の変数 lines に取り込み、保存しておくとします。
そして、 lines の内容を右のリストに表示するような例ですね。

本題

レーベンシュタイン距離とパスの利用例として、先述の例2のパターンで、レーベンシュタイン距離とパスを使って、配列と同期した別データ(GUIのリストの内容)の更新を行います
ここでは、GUIライブラリには GtkD を使用することとします。

import gtk.Main, gtk.MainWindow, gtk.Box;
import gtk.TextView, gtk.TextBuffer, gtk.TextTagTable;
import gtk.TreeView, gtk.ListStore, gtk.TreeIter, gtk.TreeViewColumn, gtk.CellRendererText;
import std.string;

/// テキストの更新前後をもとに、リストを更新する
void updateListByLines(ref string[] linesBefore, string[] linesAfter, ListStore list)
{
    TreeIter itr;

    // 要素全消し
    list.clear();
    // 全部の行を追加しなおす
    foreach (line; linesAfter)
    {
        list.append(itr);
        list.setValue(itr, 0, line);
    }

    linesBefore = linesAfter;
}

void main(string[] args)
{
    Main.init(args);
    auto win = new MainWindow("Edit and List");
    auto box = new Box(GtkOrientation.HORIZONTAL, 6);
    auto edit = new TextView;
    auto list = new TreeView(new ListStore([GType.STRING]));
    list.appendColumn(new TreeViewColumn("Test", new CellRendererText, "text", 0));
    list.setHeadersVisible(false);

    string[] lines;
    edit.getBuffer.addOnChanged((TextBuffer buf)
    {
        lines.updateListByLines(
            buf.getText().splitLines(),
            cast(ListStore)list.getModel());
    });

    box.packStart(edit, true, true, 0);
    box.packStart(list, true, true, 0);
    win.add(box);

    win.showAll();
    Main.run();
}

updateListByLinesという関数が今回のポイントです。テキストの更新前後をもとに、リストの内容を更新する関数です。
GUIでリストボックスの操作はそれなりに時間がかかりそうで、上記のように配列が更新されるたびにいちいち全消ししてから全部追加とかしていたら明らかに時間がかかりそう。たった数個の配列であればまだしも、数が増えて数千～数万の要素となった場合、たった一つ更新しただけで真っ白の画面で数秒フリーズしてたんじゃ話になりませんね。

以下に、レーベンシュタイン距離とパス(levenshteinDistanceAndPath)を用いて、上記関数(updateListByLines)の改良例を示します。

/// テキストの更新前後をもとに、リストを更新する
void updateListByLines(ref string[] linesBefore, string[] linesAfter, ListStore list)
{
    import std.algorithm, std.stdio;
    TreeIter itr;
    size_t indexBefore, indexAfter;

    // レーベンシュタイン距離とパスから、パスを取り出す
    auto levPath = levenshteinDistanceAndPath(linesBefore, linesAfter)[1];
    // 全部の編集内容に対する処理
    foreach (editOp; levPath) final switch (editOp)
    {
    case EditOp.none:
        // 何もしない
        writefln("EditOp.none: [%s]%s -> [%s]%s",
            indexBefore, linesBefore[indexBefore],
            indexAfter,  linesAfter[indexAfter]);
        indexBefore++;
        indexAfter++;
        break;
    case EditOp.insert:
        // アイテムの挿入
        if (indexBefore < linesBefore.length)
        {
            // 途中に挿入する場合
            writefln("EditOp.insert: [%s]%s -> [%s]%s",
                indexBefore, linesBefore[indexBefore],
                indexAfter,  linesAfter[indexAfter]);
            list.insert(itr, cast(int)indexBefore);
            list.setValue(itr, 0, linesAfter[indexAfter]);
        }
        else
        {
            // 最後に挿入する(拡張する)場合
            writefln("EditOp.insert: [%s](none) -> [%s]%s",
                indexBefore,
                indexAfter, linesAfter[indexAfter]);
            list.insert(itr, -1);
            list.setValue(itr, 0, linesAfter[indexAfter]);
        }
        indexAfter++;
        break;
    case EditOp.substitute:
        // アイテムの内容を変更する
        writefln("EditOp.substitute: [%s]%s -> [%s]%s",
            indexBefore, linesBefore[indexBefore],
            indexAfter,  linesAfter[indexAfter]);
        list.iterNthChild(itr, null, cast(int)indexBefore);
        list.setValue(itr, 0, linesAfter[indexAfter]);
        indexBefore++;
        indexAfter++;
        break;
    case EditOp.remove:
        // アイテムを削除する
        writefln("EditOp.remove: [%s]%s",
            indexBefore, linesBefore[indexBefore]);
        list.iterNthChild(itr, null, cast(int)indexBefore);
        list.remove(itr);
        indexBefore++;
        break;
    }

    linesBefore = linesAfter;
}

わかりやすさのために、writeflnを用いて、どんな操作によって、何行目のどんな文字列が、何番目のどんな文字列に変更されたか、について表示するようにしています。

レーベンシュタイン距離とパスから、パスを取り出す

下記のようにして取り出します。

auto levPath = levenshteinDistanceAndPath(linesBefore, linesAfter)[1];

levenshteinDistanceAndPathには、変更前の配列と、変更後の配列を渡します。
戻り値はレーベンシュタイン「距離(size_t型)」と、「パス(EditOp[]型)」がTuple型になって返ります。
今回の例では距離は不要で、パスについてのみ扱うため、添え字に[1]として、パスだけを取り出します。

全部の編集内容に対する処理

foreach (editOp; levPath) final switch (editOp)
{
case EditOp.none:
    // 何もしない
    ...
    indexBefore++;
    indexAfter++;
case EditOp.insert:
    // アイテムの挿入
    ...
    indexAfter++;
case EditOp.substitute:
    // アイテムの内容を変更する
    ...
    indexBefore++;
    indexAfter++;
case EditOp.remove:
    // アイテムを削除する
    ...
    indexBefore++;
}

上記のようにし、パスに含まれるすべての各編集内容(EditOp)について行う処理を実装します。ほとんど定型文みたいなものだと思っていいです。
編集前の配列にアクセスするための添え字indexBeforeと、編集後の配列にアクセスするための添え字indexAfterを使って、それぞれlinesBefore[indexBefore], linesAfter[indexAfter] のようにして変更前後の要素にアクセスします。

各編集内容にて、実施するべき内容

EditOp.none
変更されなかった要素です。 何もせず、indexBeforeと、indexAfterを一つ進めます。
EditOp.insert
新しく挿入されている要素です。「挿入」に対する処理を行います。 新しく追加された要素のため、linesBefore[indexBefore]はここでは使えません。また、編集後の配列の要素だけが増えるため、indexAfterのみ一つ進めます。
EditOp.substitute
内容が変更された要素です。「変更」に対する処理を行い、indexBeforeと、indexAfterを両方一つ進めます。また、「変更」に対する処理が難しい場合(反映させたい対象にreplace関数など操作が存在しない場合など)、「挿入」して「削除」するようにするとほぼ等価の処理内容となります。
EditOp.remove
編集前にはあって、編集後には無くなった、削除された要素です。「削除」に対する処理を行います。削除された要素であるため、linesAfter[indexAfter]はここでは使えません。また、編集後の配列は減るため、indexBeforeのみ一つ進めます。

各処理を実施したあとで、linesBefore = linesAfter;として、配列を更新します。

まとめ

  • レーベンシュタイン距離とパスを使うことで、差分を抽出できる
  • 編集前の配列Aと編集後の配列Bを使って、更新対象Cを更新するために使える。
  • 更新対象Cは、全消し＆全追加すると遅くなる、という場合に有効
  • レーベンシュタイン距離とパスで更新対象Cを差分更新するのに最低限必要な処理は、「挿入(insert/replaceなどのメソッド)」「削除(remove/deleteなどのメソッド)」で、「変更(replace/substitute/setなどのメソッド)」はあるとより良いが「挿入」と「削除」で代替可能。
  • 今回紹介したポトペタコードで、簡単に高速化できる
6
5
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
6
5