AIを実践する上で必要な基礎的な数学のうち、重要な3点に絞ってまとめてみました。
私自身が大学1、2年のときに学んだ線形代数の知識の整理、復習という意味合いもあります。
1.線形代数
基本的な行列の演算については、ここでは省略します。
ここでは、そのなかでも特異値分解に的を絞ります。
固有値は聞いたことがあるけど、特異値って何?という人もいると思います。
ここでは、行列の基本的な演算や逆行列の計算については理解していることを前提としています。
1-1 まずは固有値、固有ベクトルのおさらい
特異値分解は、どんな行列にも対応できるようにした固有値分解の一般化バージョンです。
ですので、まずは固有値分解の復習をします。
簡単のため三次の正方行列について考えます。
行列$A$を
A=
\begin{pmatrix}
a_{11} & a_{12} &a_{13} \\
a_{21} & a_{22} &a_{23} \\
a_{31} & a_{32} &a_{33}
\end{pmatrix}
とおきます。
A\vec{x}=λ\vec{x} ・・・(1)\\
を満たすスカラー$λ$、とベクトル$\vec{x}$があるとき、前者を固有値、後者を固有ベクトルと呼びます。
\vec{x}=
\begin{pmatrix}
x_1 \\
x_2 \\
x_3
\end{pmatrix}
このような固有値、固有ベクトルを求める問題を固有値問題といいます。固有多項式$det|A-λI|=0$を解けば、この$λ$を求めることができます。$I$は単位行列です。
1-2 固有値、固有ベクトルを求めて、何がうれしいのか。
固有値、固有ベクトルを使うと、対角行列を求めることができます。
*対角化できないことも勿論ありますが、その場合は対角行列に似た形のJordan標準形にする方法があります。
(詳細は数多ある専門書や他サイトをご参照ください。)
例えば、
A=
\begin{pmatrix}
2 & 1 &1 \\
1 & 2 &1 \\
1 & 1 &2
\end{pmatrix}
の固有値は、固有方程式を解くと、$λ_1=4,λ_2=1,λ_3=1$と求まります。これに対応する固有ベクトルは式(1)より、
\vec{p_1}=
\begin{pmatrix}
1 \\
1 \\
1
\end{pmatrix},
\vec{p_2}=
\begin{pmatrix}
-1 \\
1 \\
0
\end{pmatrix},
\vec{p_3}=
\begin{pmatrix}
-1 \\
0 \\
1
\end{pmatrix}
と求めることができます。これらのベクトルを並べてできる正方行列$P=[p_1\ p_2\ p_3]$を用いると、
P^{-1}AP=
\begin{pmatrix}
4 & 0 &0 \\
0 & 1 &0 \\
0 & 0 &1
\end{pmatrix}
と対角化することができます。
1-3 特異値、特異ベクトルについて
さきほど述べたとおり、正方行列の場合、固有値分解すなわち、対角化(あるいはJordan標準形に)することができます。
一方、正方行列でない行列も含めた任意の行列について行列分解する手法が、これから記述する特異値分解(Singular Value Decomposition;SVD)です。
ここで、簡単のために3行2列の行列$A$について考えます。
A
=
\begin{pmatrix}
3 & 1 \\
\sqrt{10} & \sqrt{10} \\
1 & 3 \\
\end{pmatrix}
,\
A^T=
\begin{pmatrix}
3 & \sqrt{10} &1 \\
1 & \sqrt{10} &3 \\
\end{pmatrix}
について、特異値分解を行います。
右特異ベクトルを求めるために、
A^TA=
\begin{pmatrix}
20 & 16 \\
16 & 20 \\
\end{pmatrix}
の固有値を求めます。
det(λI-A^TA)=0 \\
を解くと
λ_1=36,\
λ_2=4
が得られるので、
(A^TA)\vec{v}=λ\vec{v}\\
に固有値を代入して計算すると、$λ_1=36,λ_2=4$それぞれに対応する右特異ベクトル
\vec{v_1}=
\frac{1}{\sqrt{2}}
\begin{pmatrix}
1 \\
1
\end{pmatrix}
\vec{v_2}=
\frac{1}{\sqrt{2}}
\begin{pmatrix}
1 \\
-1
\end{pmatrix}
が求まる。したがって、$A$の特異値は
σ_1=\sqrt{λ_1}=6,\
σ_2=\sqrt{λ_2}=2
であり、$σ_1=6,σ_2=2$それぞれに対応する左特異ベクトルは
\vec{u_1}=\frac{1}{σ_1}A\vec{v_1}=
\frac{1}{3\sqrt{2}}
\begin{pmatrix}
2 \\\sqrt{10}\\2
\end{pmatrix},\\
\vec{u_2}=\frac{1}{σ_2}A\vec{v_2}=
\frac{1}{\sqrt{2}}
\begin{pmatrix}
1 \\0\\-1
\end{pmatrix}
となる。ここで、
V=[\vec{v_1}\:\vec{v_2}]\\
∴V=\frac{1}{\sqrt{2}}
\begin{pmatrix}
1 & 1\\
1 & -1
\end{pmatrix}
とおけば、
A=[\vec{u_1}\:\vec{u_2}]diag[σ_1,σ_2]V^T
が成り立つ。一方で$\vec{u_1},\vec{u_2}$と直行するベクトル$\vec{u_3}$
\vec{u_3}=
\frac{1}{6}
\begin{pmatrix}
\sqrt{10} \\-4\\\sqrt{10}
\end{pmatrix}
を用いて、
U=[\vec{u_1}\:\vec{u_2}\:\vec{u_3}]\\
∴U=\frac{1}{3\sqrt{2}}
\begin{pmatrix}
2 & 3 &\sqrt{5} \\
\sqrt{10} & 0 &-2\sqrt{2} \\
2 & -3 &-3\sqrt{5}
\end{pmatrix}
とおけば、
A=UΣV^T\\
∴A=\frac{1}{3\sqrt{2}}
\begin{pmatrix}
2 & 3 &\sqrt{5} \\
\sqrt{10} & 0 &-2\sqrt{2} \\
2 & -3 &-3\sqrt{5}
\end{pmatrix}
\begin{pmatrix}
6 & 0 \\
0 & 2 \\
0 & 0 \\
\end{pmatrix}
\frac{1}{\sqrt{2}}
\begin{pmatrix}
1 & 1\\
1 & -1
\end{pmatrix}
が成り立つ。
2.確率統計
確率統計の分野でも、よく出てくるベイズの定理について、理解したのでここでまとめます。
2-1ベイズの定理
ベイズの定理は、次の式で表現されます。
P(A|B)=\frac{P(B|A)P(A)}{P(B)}・・・(2)
ここで、$P(A|B)$とは、事象Bのもとで、事象Aが起こる確率のことで「条件付き確率」と呼びます。証明は至ってシンプルです。
事象Aと事象Bが同時に起こる確率を$P(A∧B)$とすると、
P(A∧B)=P(A)P(B|A)\\
P(A∧B)=P(B)P(A|B)
と表現できますので、$P(A∧B)$を消去することにより、ベイズの定理が導かれます。
この定理から、有用なベイズの展開公式を導くことができます。
ここで、事象Bが事象$C_1$あるいは事象$C_2$のみを原因として生じるとします。また、事象$C_1$と事象$C_2$は排反とします。つまり、事象$C_1$と事象$C_2$が同時に起きることはないとします。
すると、事象$B$が生じる確率は、下記のように表現できます。
(Bが生じる確率)=(C_1を原因としてBが生じる確率)+(C_2を原因としてBが生じる確率)\\
P(B)=P(B|C_1)P(C_1)+P(B|C_2)P(C_2)\\
これを式(2)に代入すると、下記のベイズの展開公式が得られます。
P(A|B)=\frac{P(B|A)P(A)}{P(B|C_1)P(C_1)+P(B|C_2)P(C_2)}・・・(3)\\
2-2ベイズの定理の例題
さて、ここではベイズの定理を理解するために、例題を解いてみます。
ここでは、タロットカードからカードを引く例に話を進めて行きます。
タロットカードは78枚を1組としたカードで、寓意画が描かれた22枚の「大アルカナ」と56枚の小アルカナに分けられます。小アルカナは、更に14枚を1組とした4つのスート(杖、杯、剣、硬貨)に分けられます。それぞれのスートは、1~10の数字が書かれた数札と人物が描かれた人物札に分けられます。
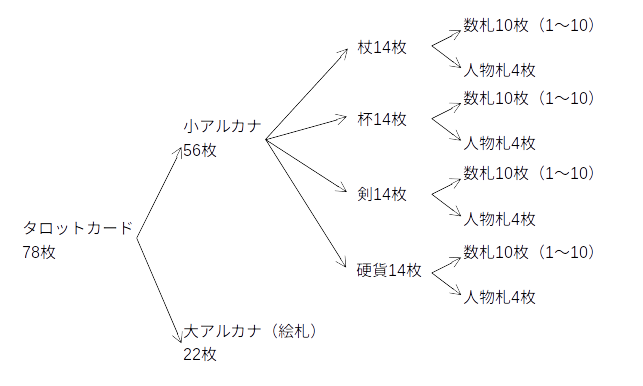
では、ここで本題に移ります。
78枚1組のタロットカードをシャッフルして、1枚めくるとします。めくったカードが数札であったとき、スートが剣である確率(条件確率)をベイズの定理を使って計算してみます。求める確率は、スートが剣であり、かつ数札である確率(同時確率)でないことに注意しましょう。
ここで、ベイズの展開公式(3)を用いると、
P(剣|数)=\frac{P(数|剣)P(剣)}{P(数|杖)P(杖)+P(数|杯)P(杯)+P(数|剣)P(剣)+P(数|硬貨)P(硬貨)}\\
P(剣|数)=\frac{\frac{10}{14}×\frac{1}{4}}{\frac{10}{14}×\frac{1}{4}+\frac{10}{14}×\frac{1}{4}+\frac{10}{14}×\frac{1}{4}+\frac{10}{14}×\frac{1}{4}}=\frac{1}{4}
もちろん、ベイズの定理を使わなくても、計算は可能です。
2-3ベイジアンネットワークの例題
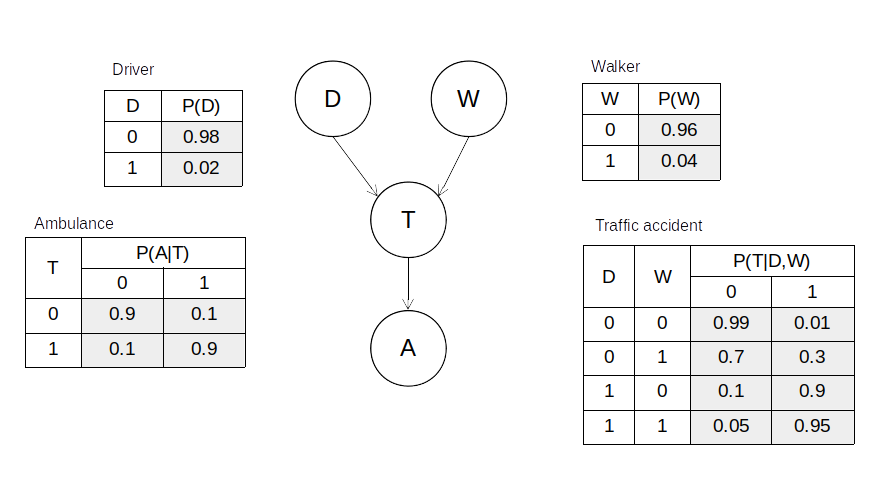
「風が吹けば桶屋が儲かる」というように、ある事象は過去に起こった事象を原因として、次から次に確率的に起こっていくと考えることができます。この考えと先程のベイズの定理を組み合わせると、多数の事象が連鎖的に繋がったベイジアンネットワークを構成することができ、様々な分野で応用されています。例として、次のような交通事故の例を考えてみます。
交通事故(T:Traffic Accident)が、運転手(D:Driver)側の過失と歩行者(W:Walker)側の過失によって起こり、救急車が呼ばれるという一連のながれをモデル化したとき、それは下記のように図示できます。
運転手側の過失としては脇見や飲酒運転、歩行者側の過失としては信号無視や横断歩道以外の場所での横断等があるかと思います。そうした過失をする確率をそれぞれ、$P(D)$、$P(W)$と置きます。また、過失をした条件下での交通事故の発生確率は、$P(T|D,W)$と起きます。さらに、交通事故が発生した条件下で救急車(A:Ambulance)が呼ばれる確率は$P(A|T)$とします。交通事故以外で救急車が呼ばれる原因は、急病等いろいろと考えられますが、ここでは簡単のために原因を交通事故のみとします。急病(S:Sick)も原因として考えるならば、Aのノードの直前の位置に、Sのノードを付け加えれば良いだけです。さて、ここで救急車(A)が呼ばれたときに、その原因がドライバー(D)の過失による事故である確率$P(D|A)$を考えてみます。
ベイズの定理より、
P(D|A)=\frac{P(A∩D)}{P(A)}・・・(4)
また、
P(A)=P(A∩T)+P(A∩\bar{T})
であるから、
P(A)=P(A|T)P(T)+P(A|\bar{T})P(\bar{T})・・・(5)
次に、$P(T),P(\bar{T})$を求めます。
P(T)=P_1+P_1+P_2+P_3+P_4\\
P_1=P(T|D,W)P(D)P(W)=0.009408\\
P_2=P(T|D,\bar{W})P(D)P(\bar{W})=0.01176\\
P_3=P(T|\bar{D},W)P(\bar{D})P(W)=0.01728\\
P_4=P(T|\bar{D},\bar{W})P(\bar{D})P(\bar{W})=0.00076\\
∴P(T)=0.039208
P(\bar{T})=1-0.039208=0.960792
式(5)に代入して
P(A)=0.9×0.039208+0.1×0.960792=0.1313664
P(A∩D)=P((A∩D)∩(T∪\bar{T}))\\
\qquad\qquad\qquad\qquad=P(A∩D∩T)+P(A∩D∩\bar{T})\\
\qquad\qquad\qquad\qquad\qquad\quad=P(A∩D|T)P(T)+P(A∩D|\bar{T})P(\bar{T})\\
\qquad\qquad\qquad\qquad\qquad\qquad\qquad=P(A|T)P(D|T)P(T)+P(A|\bar{T})P(D|\bar{T})P(\bar{T})\\
\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad=P(A|T){P(T)P(D|T)}+P(A|\bar{T}){P(\bar{T})P(D|\bar{T})}\\
\qquad\qquad\qquad\qquad\qquad\qquad\qquad=P(A|T)P(D)P(T|D)+P(A|\bar{T})P(D)P(\bar{T}|D)\\
\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad=P(A|T)P(D){P(T|D,W)P(W)+P(T|D,\bar{W})P(\bar{W})}+\\
\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad P(A|\bar{T})P(D){P(\bar{T}|D,W)P(W)+P(\bar{T}|D,\bar{W})P(\bar{W})}
これを計算すると、
P(A∩D)=0.016432
(4)式より、
P(D|A)=0.125085
3.情報理論
次に、カルバックライブラー情報量について事例とともに考えてみます。
3-1検査手法の例
ある感染症に感染しているかどうかを診断する2種類の検査A,Bがあったとします。この2種類の検査の有効性を調べるために、試験をした結果、下記のような結果が得られました。このとき、どちらの検査の方が正確でしょうか。
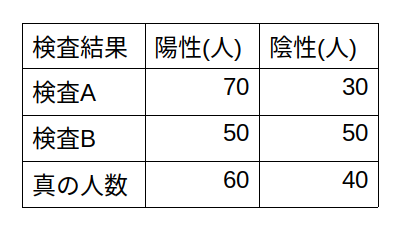
これを確率として計算すれば、下表のようにまとめられます。

また、縦軸を確率p横軸を確率qとしてグラフ化してみると下記のようになります。
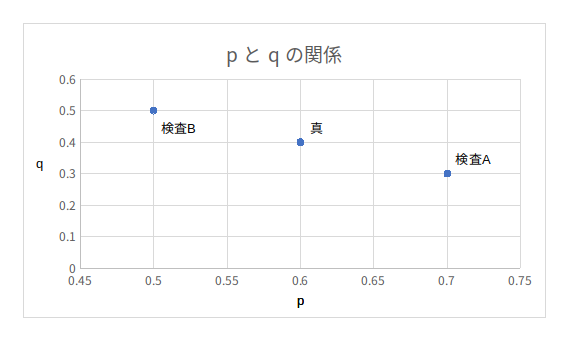
こうして表とグラフを眺めてみると、真の比率からは等しく離れているように見えます。
また、この試験結果は下記のようにブレークすることができます。
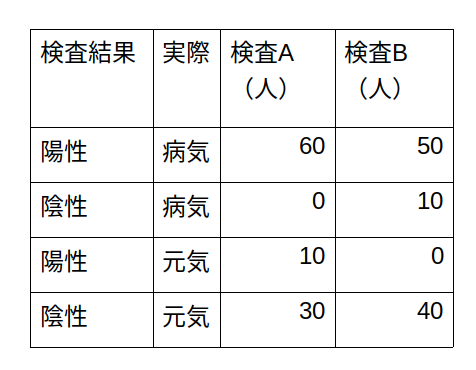
3-2用語の定義
情報理論の計算で用いる用語について、ここで整理します。A,Bが出てきますが、上記の検査A、Bとは関係ありませんので、ご注意ください。
・情報量 :情報を知ることによって得られる不確定さの減少度合い。
・自己情報量 :$I(A)=-log(P(A))$。$P(A)$は事象Aが生じる確率。つまり確率が小さい(Aという事象が起こりにくい)ほど、自己情報量は大きい。明日の天気が晴れという自己情報量よりも地球に隕石が衝突するという自己情報量の方が大きい。
・情報エントロピー:自己情報量の期待値。平均情報量とも。
$H(A)=-ΣP(A)×I(A)$。
・交差(クロス)エントロピー:事象B(あるいはA)に関する情報を、事象A(あるいはB)を知ることによって得られるとした場合の情報量の期待値。
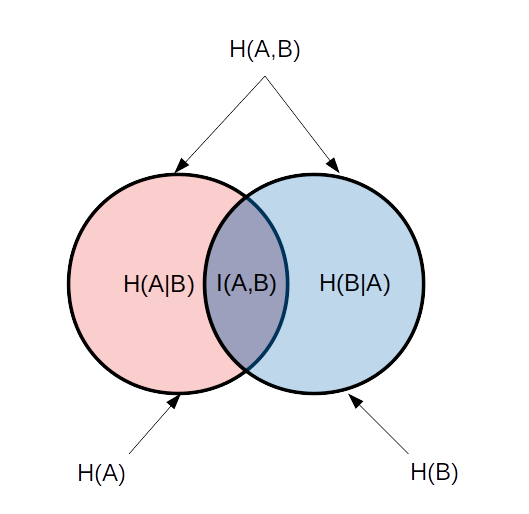
$H(A,B)=-ΣP(A)×I(B)=-ΣP(B)×I(A)$。あるいは、$H(A,B)=H(A)+H(B|A)=H(B)+H(A|B)$
・相互情報量:事象A(あるいはB)に関する情報を知ることによって得られる事象B(あるいはA)に関する情報量。
$I(A,B)=H(B)-H(B|A)=H(A)-H(A|B)$。
例えば、事象Aをサイコロで偶数の目{2,4,6}が出る事象。事象Bを3の倍数の目{3,6}が出る事象とする。$H(B)=log(3)$、$H(B|A)=log(3)$より、$I(A,B)=0$。つまり、偶数であるという情報を得たところで、3の倍数であるという情報は変わらない。
・カルバックライブラー(KL)情報量:$D(p,q)=Σp_ilog\frac{p_i}{q_i}$。確率分布間のギャップ。
・情報量の単位 :対数の底が2のときビット。対数の底が10のときデジット。対数の底が$e$のときナット。
ベン図を描いて整理してみます。
3-3カルバックライブラー情報量の計算
検査Aの診断結果と真の割合とのKLダイバージェンス
$D(A,真)=-(0.6log0.7+0.4log0.3)+(0.6log0.6+0.4log0.4)=0.0226$
$D(B,真)=-(0.6log0.5+0.4log0.5)+(0.6log0.6+0.4log0.4)=0.0201$
したがって、検査Bから得られる情報の方が実際の情報に近い結果が得られる。
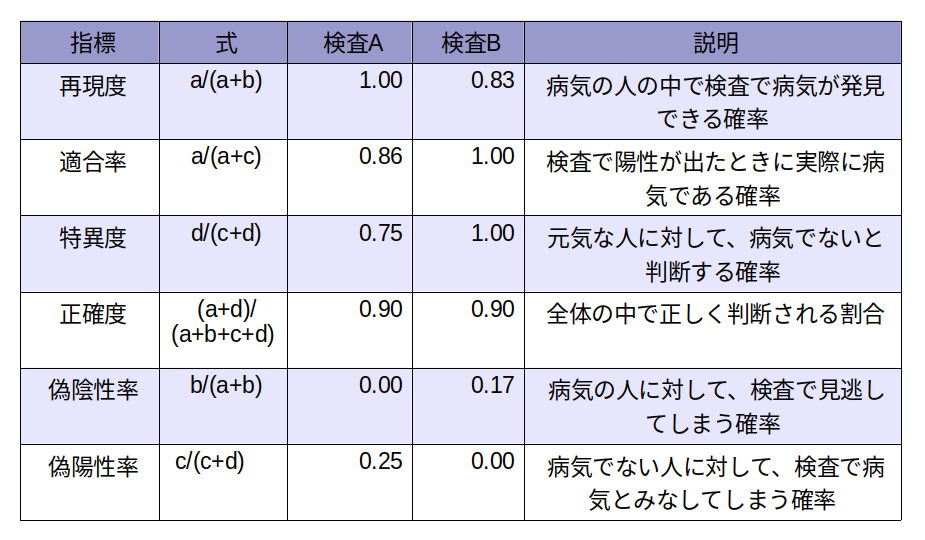
3-4検査の評価指標
・病気で陽性反応が出た人の数 :a(人)
・病気なのに陰性反応が出た人の数 :b(人)
・元気なのに陽性反応が出てしまった人の数:c(人)
・元気で陰性反応が出た人の数 :d(人)
とすると、下表の指標が得られます。
このように、実際問題として分布が近いということも重要だと思いますが、検査Bで見逃すリスクを許容するよりも、検査Aで診断後に陽性であれば、さらに精密検査を受診というのが良いような気がします。医療関係者ではありませんので、そのあたりのことは詳しくわかりませんが。
注
・余談ですが、特異値分解において、なるべく計算が楽になるような行列$A$を探すのに結構苦労しました。
・尚、今回の投稿はE検定対策講座のレポート課題として、作成されたものです。この講座は、あくまでも機械学習を学ぶ人のきっかけを作るという意味で有意です。http://ai999.careers/rabbit/