k-means++初期化の概要
k-means++でやりたいこと
k-meansではデータ構造自体からデータをクラスタリングする。inputとして教師データは不要で、クラスタリングするクラス数と初期クラス中心点を指定する。
この初期クラス位置が重要で、k-meansアルゴリズムの性質上、そのとり方によって結果が変わってしまう。k-means++では初期値を良い感じに配置するためのアルゴリズムを与える。
一言でいうと、中心点が、データ点の集合のなかでいい感じに分散するようなアルゴリズムである。
k-means++の初期化についての概念と簡単な実装はPythonでの数値計算ライブラリNumPy徹底入門 - DeepAgeがとてもわかりやすい。
ここでは実際の実装(sklearn)におけるk-means++の初期化アルゴリズムを調べる。
初期化では何をしているのか?
やりたいことは、外れ値に強く、かつ各中心点を適度にばらつかせること。
一番最初の中心点はデータ点からランダムに一点を選ぶ。空間からランダムに選ぶのではなく、データ点から選ぶ。
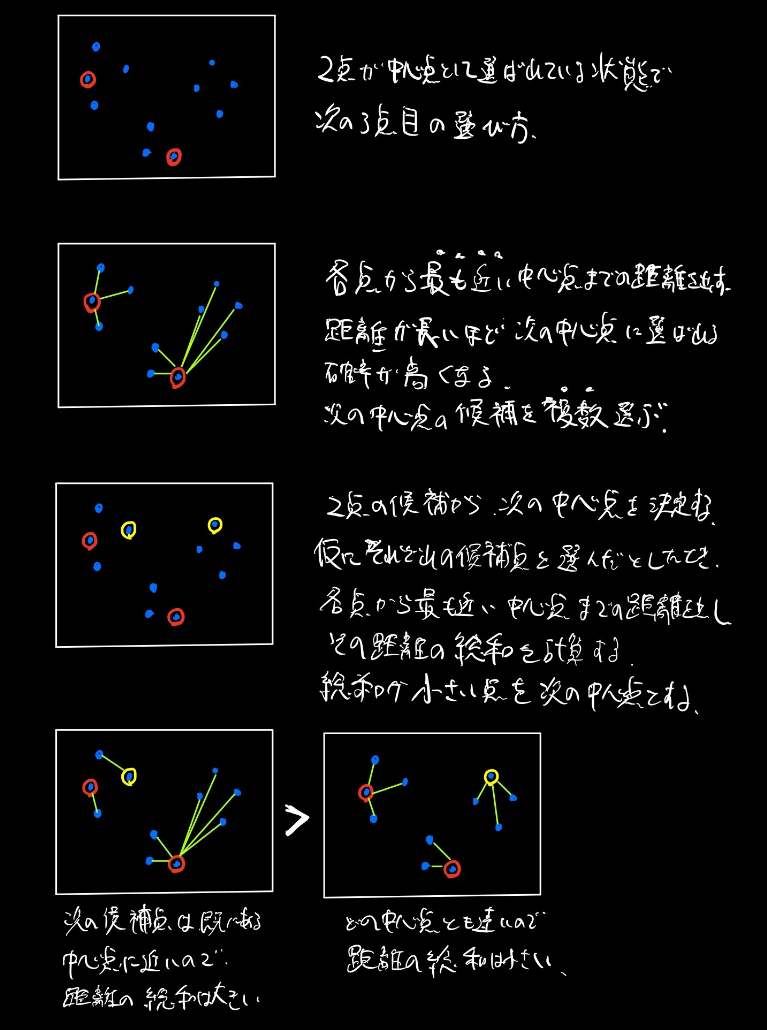
2点目以降の中心点の選び方について図で示す。
- 各点から一番近い中心点までの距離を計算する。その距離の2乗に応じて確率的に次の中心点候補を複数選ぶ。(このときすでに中心点に選ばれている点は距離が0なので選ばれる確率も0となる)。確率的に選ぶのは外れ値対策である。
- 次に複数候補点から一つを選ぶ。その基準として、各点における最近傍の中心点までの距離の和を計算する。この和が小さいほど、中心点が各データに近くなるよう配置されていることになるので、和が小さい候補点を次の中心点として採用する。今度は決定論的に最小値をとるものを採用する。
このように2つのステップを踏んで2点目以降を順次きめていく。
距離の総和を最初から使うと、計算量が増えることと、外れ値が選ばれやすくなるのがデメリットと思われる。
それでは具体的な実装をsklearnのコードで確認していく。
sklearnのk-means++の初期化のソースコード
sklearnでのk-menans++初期化処理の流れ
初期化処理の入力
- データX: array, shapeは(サンプルサイズ, 特徴次元)
- クラスター数: int
- X2乗ノルム: |X|^2, array, shapeは(サンプルサイズ, )
中心点との2乗距離を計算するときに、
|x-y|^2 = dot(x, x) - 2 * dot(x, y) + dot(y, y)
と計算するほうが効率がよいので、先に計算して引数で渡す - random_state: 最初の点をランダムに生成するのに使用する
- n_local_trials(optional): 各中心点を決めるときの候補の数. defaultは(2+log(k))
最初の中心点をデータ点の中からランダムに選ぶ
特徴空間全体からランダムに選ぶのではなく、データ点の一つを選ぶ
center_id = random_state.randint(n_samples)
centers[0] = X[center_id]
各点から中心点との距離と、その距離の総和を計算する
どちらも次の候補点選びに使われる
closest_dist_sq = euclidean_distances(
centers[0, np.newaxis], X, Y_norm_squared=x_squared_norms,
squared=True)
current_pot = closest_dist_sq.sum() # potはpotentialのpot
次の候補点を複数(n_local_trials)選ぶ
やりたいことは最近房の中心点までの距離の2乗に応じて確率的に選択するということ。つまり距離0、距離2、距離4の3点があるとすると、それぞれ、0/(0+2^2+4^4)=0, 2^2/(0+2^2+4^4)=4/20, 4^4/(0+2^2+4^4)=16/20, の確率で選びたい。これを累積和のcumsum関数と乱数を使って実現している. 総和×(0-1乱数)がcumsumのどこにぶつかるか、という感じで、距離が大きいほど選ばれやすくなる.
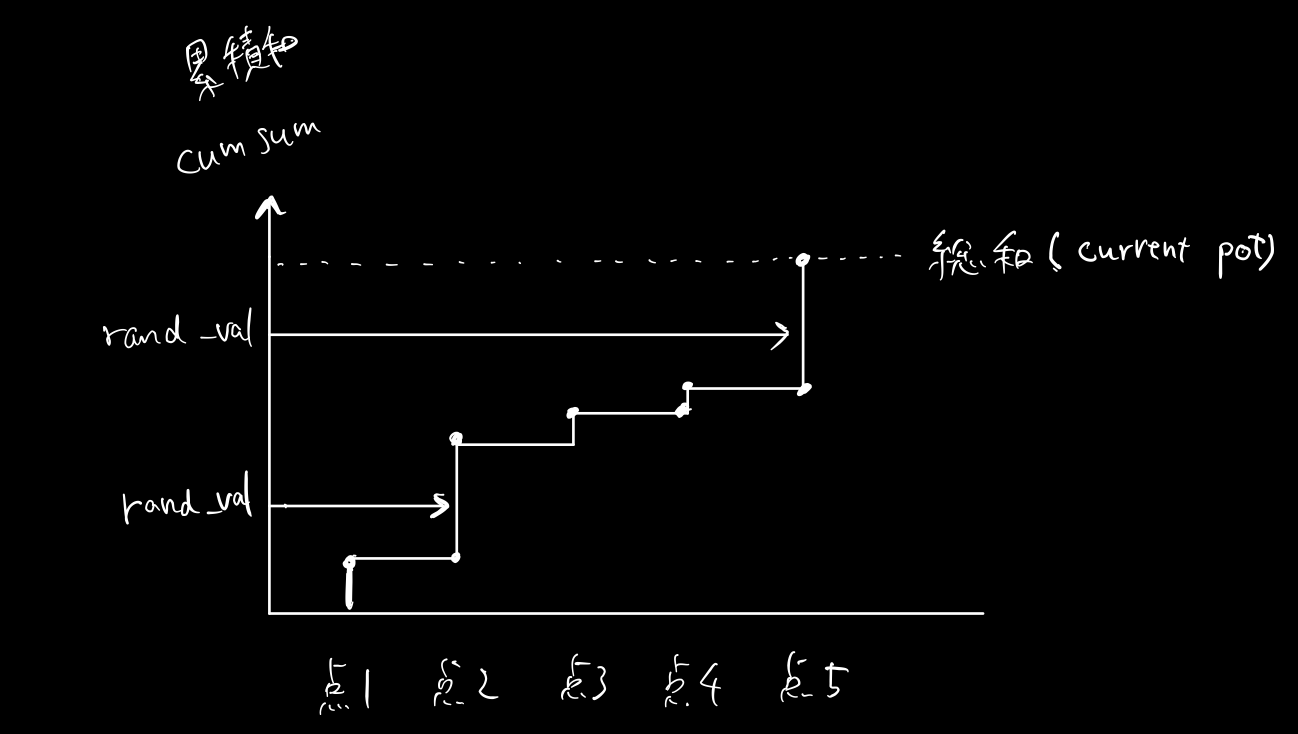
rand_vals = random_state.random_sample(n_local_trials) * current_pot
candidate_ids = np.searchsorted(stable_cumsum(closest_dist_sq), rand_vals)
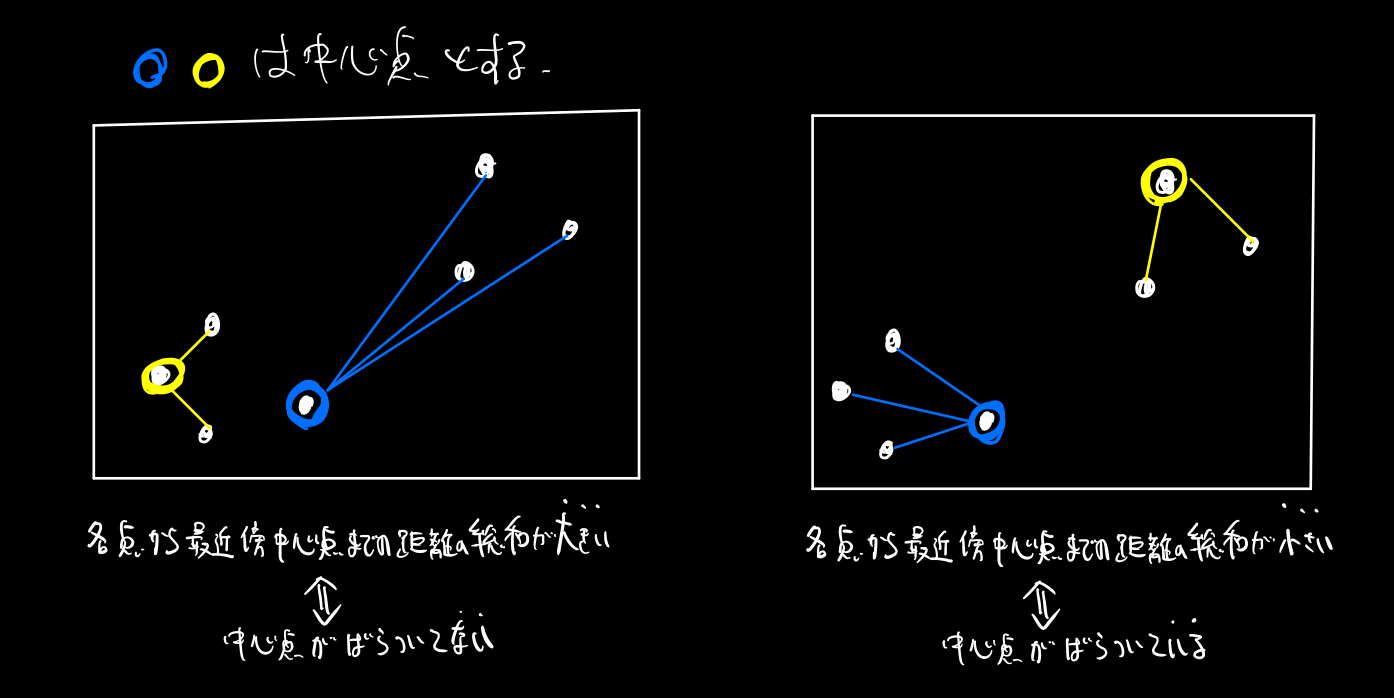
候補点から一つを次の中心点として選ぶ
各点における最近傍の中心点までの距離の和が小さいほど、中心点が各データに近くなるよう配置されていることになるので、和が小さい候補点を次の中心点として採用する。
採用したら前の節の処理に戻り、全ての点を選ぶまで複数選択→決定の処理を繰り返す。
for trial in range(n_local_trials):
# Compute potential when including center candidate
new_dist_sq = np.minimum(closest_dist_sq, distance_to_candidates[trial])
new_pot = new_dist_sq.sum()
# Store result if it is the best local trial so far
if (best_candidate is None) or (new_pot < best_pot):
best_candidate = candidate_ids[trial]
best_pot = new_pot
best_dist_sq = new_dist_sq
ソースコード全体
# scikit-learn/sklearn/cluster/k_means_.py 2019-11-3
def _k_init(X, n_clusters, x_squared_norms, random_state, n_local_trials=None):
"""Init n_clusters seeds according to k-means++
Parameters
----------
X : array or sparse matrix, shape (n_samples, n_features)
The data to pick seeds for. To avoid memory copy, the input data
should be double precision (dtype=np.float64).
n_clusters : integer
The number of seeds to choose
x_squared_norms : array, shape (n_samples,)
Squared Euclidean norm of each data point.
random_state : int, RandomState instance
The generator used to initialize the centers. Use an int to make the
randomness deterministic.
See :term:`Glossary <random_state>`.
n_local_trials : integer, optional
The number of seeding trials for each center (except the first),
of which the one reducing inertia the most is greedily chosen.
Set to None to make the number of trials depend logarithmically
on the number of seeds (2+log(k)); this is the default.
Notes
-----
Selects initial cluster centers for k-mean clustering in a smart way
to speed up convergence. see: Arthur, D. and Vassilvitskii, S.
"k-means++: the advantages of careful seeding". ACM-SIAM symposium
on Discrete algorithms. 2007
Version ported from http://www.stanford.edu/~darthur/kMeansppTest.zip,
which is the implementation used in the aforementioned paper.
"""
n_samples, n_features = X.shape
centers = np.empty((n_clusters, n_features), dtype=X.dtype)
assert x_squared_norms is not None, 'x_squared_norms None in _k_init'
# Set the number of local seeding trials if none is given
if n_local_trials is None:
# This is what Arthur/Vassilvitskii tried, but did not report
# specific results for other than mentioning in the conclusion
# that it helped.
n_local_trials = 2 + int(np.log(n_clusters))
# Pick first center randomly
center_id = random_state.randint(n_samples)
if sp.issparse(X):
centers[0] = X[center_id].toarray()
else:
centers[0] = X[center_id]
# Initialize list of closest distances and calculate current potential
closest_dist_sq = euclidean_distances(
centers[0, np.newaxis], X, Y_norm_squared=x_squared_norms,
squared=True)
current_pot = closest_dist_sq.sum()
# Pick the remaining n_clusters-1 points
for c in range(1, n_clusters):
# Choose center candidates by sampling with probability proportional
# to the squared distance to the closest existing center
rand_vals = random_state.random_sample(n_local_trials) * current_pot
candidate_ids = np.searchsorted(stable_cumsum(closest_dist_sq),
rand_vals)
# XXX: numerical imprecision can result in a candidate_id out of range
np.clip(candidate_ids, None, closest_dist_sq.size - 1,
out=candidate_ids)
# Compute distances to center candidates
distance_to_candidates = euclidean_distances(
X[candidate_ids], X, Y_norm_squared=x_squared_norms, squared=True)
# Decide which candidate is the best
best_candidate = None
best_pot = None
best_dist_sq = None
for trial in range(n_local_trials):
# Compute potential when including center candidate
new_dist_sq = np.minimum(closest_dist_sq,
distance_to_candidates[trial])
new_pot = new_dist_sq.sum()
# Store result if it is the best local trial so far
if (best_candidate is None) or (new_pot < best_pot):
best_candidate = candidate_ids[trial]
best_pot = new_pot
best_dist_sq = new_dist_sq
# Permanently add best center candidate found in local tries
if sp.issparse(X):
centers[c] = X[best_candidate].toarray()
else:
centers[c] = X[best_candidate]
current_pot = best_pot
closest_dist_sq = best_dist_sq
return centers