多変量解析入門の書籍を元に、各種分析の理論的背景を整理し、pythonで実行結果を確認します。本のまんまです。
単回帰分析
回帰分析の入門的位置
実務ではやくに立たないが、単回帰分析の理論的説明は重回帰分析の理解に必要となる。
実際はエクセルやスプレッドシートで単回帰分析の仕方をググれば簡単に試すことが可能。
単回帰分析は説明変数1つで目的変数の予測を行う。
導入
あるサイトのページビューxとCV数yの関係を調べるために、n=10のデータがある。
x = [71, 81, 86, 72, 77, 73, 80, 81, 85, 74]
y = [2.2, 4.1, 5.5, 1.9, 3.4, 2.6, 4.2, 3.7, 4.9, 3.2]
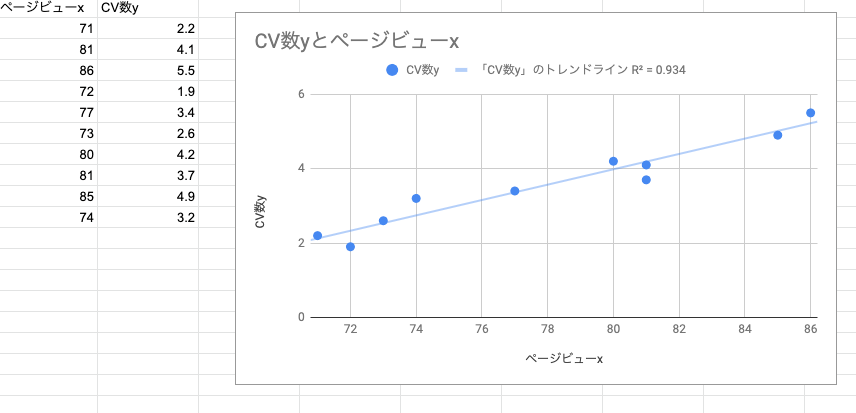
spreadsheetで解析した結果
ページビュー数が増えるにつれて、CV数も増えている関係が見て取れます。図で直線が引かれていますが、この直線をデータから求めます。
解析ストーリ
解析のストーリを以下に示します。
(1) 単回帰モデル
y_{i}=\beta_{0}+\beta_{1}x_{i}+\epsilon_{i}, \epsilon_{i} \sim N(0,σ^2)
(誤差$\epsilon_{i}$は互いに独立に$N(0, σ^2)$に従う)を想定し、回帰母数$\beta_{0}$と$\beta_{1}$を最小二乗法で推定する。
(2) 寄与率や自由度調整寄与率を求めて(1)で得られた回帰式の性能を評価する
(3) 回帰係数$\beta_{1}$について検定・区間推定を行う
(4) 残差とてテコ比の検討を行い、得られた回帰式の妥当性を検討する
(5) 得られた回帰式を利用して、任意に指定した値x0に対して母回帰B0+B1x0を推定し、y0=B0+B1x0+e0の値を予測する。
この記事では(1) 単回帰モデルのパラメータ推定の解説を行います。
解析方法
(1) 最小二乗法による回帰式の推定
観測された$y_{i}$の値は$\beta_{0}+\beta_{1}x_{i}$のパラメータ$\beta_{0}と\beta_{1}$によって決まる。このパラメータを使って直線を求めることから始める。このパラメータを求めるために、最小二乗法を使用する。
求める直線を
\hat{y}=\hat{\beta_{0}}+\hat{\beta_{1}}x
とおく。実際のデータを当て込み
\hat{y_{i}}=\hat{\beta_{0}}+\hat{\beta_{1}}x_{i}
とする。${\hat{y_{i}}}$を予測値と呼び、実測値($y_{i}$)と区別する。実測値と予測値の差を残差と呼ぶ。つまり残差$\epsilon_{i}$は
\epsilon_{i} = y_{i} - \hat{y_{i}} = y_{i} - (\beta_{0}+\beta_{1}x_{i})
となり、そして次の残差平方和が最小になる$\beta_{0}$と$\beta_{1}$を求める。
S_{e} = \sum_{i=1}^{n}e_i^2 = \sum_{i=1}^{n}\left\{y_{i} - (\beta_{0}+\beta_{1}x_{i})\right\}^2
そのためには、$S_{e}$を偏微分して0となる箇所が答えになるので、それぞれ、
\frac{\partial S_{e}}{\partial \beta_{0}} = -2\sum_{i=1}^n(y_{i}-\beta_{0}-\beta_{1}x_{i}) = 0
\frac{\partial S_{e}}{\partial \beta_{1}} = -2\sum_{i=1}^nx_{i}(y_{i}-\beta_{0}-\beta_{1}x_{i}) = 0
式を整理すると
(4.8)
\hat{\beta_{0}}n+\hat{\beta_{1}}\sum x_{i}= \sum y_{i}
(4.9)
\hat{\beta_{0}}\sum x_{i} + \hat{\beta_{1}}\sum x_i^2 = \sum x_{i}y_{i}
を得る。これを正規方程式と呼ぶ。(4.8)式より
(4.10)
\hat{\beta_{0}} = \frac{\sum y_{i}}{n} - \hat{\beta_{1}} \frac{\sum x_{i}}{n} = \overline{y}-\hat{\beta_{1}}\overline{x}
(4.10)より、$\hat{\beta_{0}}$の推定値が求まった。この式を元に$\hat{\beta_{1}}$を求めていく。(4.10)の式を(4.9)に代入すれば、
\left(\frac{\sum y_{i}}{n} - \hat{\beta_{1}} \frac{\sum x_{i}}{n}\right)\sum x_{i} + \hat{\beta_{1}}\sum x_i^2 = \sum x_{i}y_{i}
となり、整理すれば、
(4.12)
\hat{\beta_{1}}\left(\sum x_i^2-\frac{\left(\sum x_{i}\right)^2}{n}\right)=\sum x_{i}y_{i}-\frac{\sum x_{i}\sum y_{i}}{n}
を得る。ここで、xとyの偏差積和およびxの平方和
S_{xy} = \sum x_{i}y_{i}-\frac{\sum x_{i}\sum y_{i}}{n}
S_{xx} = \sum x_i^2-\frac{\left(\sum x_{i}\right)^2}{n}
を用いれば、(4.12)式より、次のように表すことができる。
\hat{\beta_1} = \frac{S_{xy}}{S_{xx}}
$\hat{\beta_1}$の値が求まった。
導出してみた(補足)
途中、偏微分から式整理までの過程がなかったので、$\beta_{0}$のみ導出してみました。
合成微分の公式より
$\mu=y_{i} - (\beta_{0}+\beta_{1}x_{i})$とおくと
\sum \mu^2
このとき
\frac{\text{d}y}{\text{d}\mu}=2\sum \mu
\frac{\text{d}\mu}{\text{d}\beta_{0}}=0-1-0\times x_{i}=-1
よって、
\frac{\partial S_{e}}{\partial \beta_{0}} = 2\sum \mu \times - 1
= -2\sum \mu
= -2\sum_{i=1}^n (y_{i} - \beta_{0}-\beta_{1}x_{i}) = 0
シグマの展開公式より
-2\sum_{i_1}^n y_{i} + 2\beta_{0}n + 2\beta_{1}\sum_{i=1}^n x_{i} = 0
2\beta_{0}n + 2\beta_{1}\sum_{i=1}^n x_{i} = 2\sum_{i_1}^n y_{i}
\beta_{0}n + \beta_{1}\sum_{i=1}^n x_{i} = \sum_{i_1}^n y_{i}
ここまで
pythonで解く
求めたい直線の回帰式がこれで、
\hat{y}=\hat{\beta_{0}}+\hat{\beta_{1}}x
パラメータはそれぞれ以下で求まることがわかりました。
\hat{\beta_{0}} = \overline{y}-\hat{\beta_{1}}\overline{x}
\hat{\beta_1} = \frac{S_{xy}}{S_{xx}}
実際にpythonを使って求めてみたいと思います。改めてデータを用意
x = [71, 81, 86, 72, 77, 73, 80, 81, 85, 74]
y = [2.2, 4.1, 5.5, 1.9, 3.4, 2.6, 4.2, 3.7, 4.9, 3.2]
x,yの平均を求める
x_mean = sum(x) / len(x)
y_mean = sum(y) / len(y)
print('xの平均は{}'.format(x_mean))
print('yの平均は{}'.format(y_mean))
# xの平均は78.0
# yの平均は3.5700000000000003
xの偏差平方和を求める
s_xx = sum([(_x - x_mean) ** 2 for _x in x])
print('xの偏差平方和は{}'.format(s_xx))
# xの偏差平方和は262.0
xとyの偏差積和を求める
s_xy = sum([ (_x - x_mean) * (_y - y_mean) for (_x, _y) in zip(x, y)])
print('sとxの偏差積和は{}'.format(s_xy))
# sとxの偏差積和は54.10000000000001
$\beta_{1}$を求める
beta_1 = s_xy / s_xx
print('回帰係数は{}'.format(beta_1))
# 回帰係数は0.20648854961832064
$\beta_{0}$を求める
beta_0 = y_mean - beta_1 * x_mean
print('切片は{}'.format(beta_0))
# 切片は-12.536106870229009
ライブラリで値があってるか確認
from sklearn import linear_model
X = [[71], [81], [86], [72], [77],[73], [80], [81], [85], [74]]
Y = [[2.2], [4.1], [5.5], [1.9], [3.4], [2.6], [4.2], [3.7], [4.9], [3.2]]
clf = linear_model.LinearRegression()
clf.fit(X,Y)
print("回帰係数=", clf.coef_)
print("切片:",clf.intercept_)
回帰係数= [[0.20648855]]
切片: [-12.53610687]
あってました。