Rでsummary()を使わずに四分位数を計算する #R

概要

Rで四分位数を計算するには、summary関数やquantile関数を使えばよいです。ここでは、勉強のために四分位数をRの組み込み関数を使わずに計算してみます。

はじめに

あるデータの四分位数を知りたい場合、Rではsummary関数やquantile関数を使います。例えば、

> x <- rpois(10, 2.5)  # 個数10で平均2.5のポアソン乱数を発生してxに代入せよ
> x
 [1] 2 2 2 3 2 6 1 1 1 3

のように、まず10個の整数データをポアソン乱数をrpois関数で作ります。この生成した乱数データxの四分位数は、

> summary(x)  # 要約統計量を計算せよ
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
   1.00    1.25    2.00    2.30    2.75    6.00

のように、summary関数の出力する要約統計量から第一四分位数(1st Quantile)などが分かります。quantile関数を使っても四分位数が計算できます。

> quantile(x)  # 四分位数を計算せよ
  0%  25%  50%  75% 100% 
1.00 1.25 2.00 2.75 6.00

このようにRではコマンド1つで四分位数を計算できるのですが、勉強のためにsummary関数やquantile関数を使わずに四分位数を計算してみようと思います。

四分位数を順を追って計算する

まず、サンプルデータを用意します。サンプルデータは、標本数50、平均2.8のポアソン乱数の整数データとします。サンプルデータの設定に特に意味はありません。平均などの値は何でもよいです。

> x <- rpois(50, 2.8)
> options(width=24)  # 一行の表示文字数を24にせよ
> x
 [1] 4 3 2 1 1 1 4 3 3 0
[11] 0 4 1 4 3 3 4 0 3 2
[21] 2 2 4 0 1 1 2 1 4 1
[31] 2 2 1 6 5 3 4 3 2 5
[41] 1 2 4 3 0 2 4 2 2 0

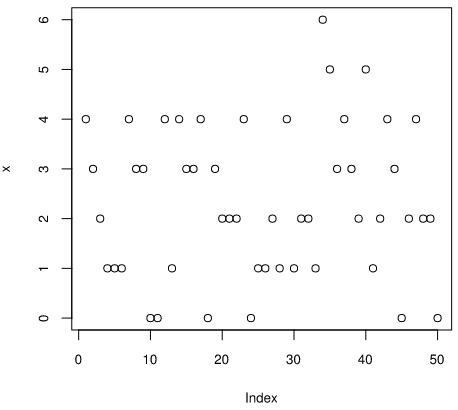
サンプルデータxの要素は0から6までの整数になりました。xをプロットすると下図になります。

> plot(x)  # xをプロットせよ

横軸はxのIndex、縦軸は各Indexの要素の値です。Index 0がありますが、xのIndexは1から50までです。50個の○が散らばっています。

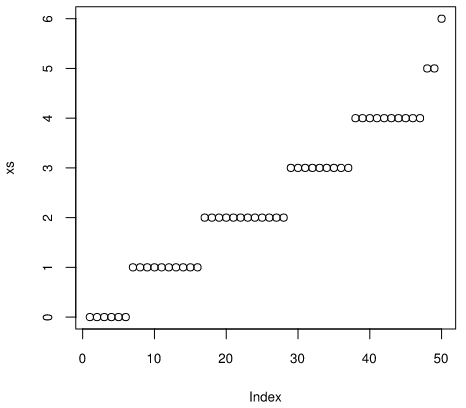
四分位数は昇順に並べ替えたデータを4等分する値なので、サンプルデータxを昇順にソートします。ソートしたデータをxsとし、xと同様にプロットします。

> xs <- sort(x)  # xを昇順にソートせよ
> xs
 [1] 0 0 0 0 0 0 1 1 1 1
[11] 1 1 1 1 1 1 2 2 2 2
[21] 2 2 2 2 2 2 2 2 3 3
[31] 3 3 3 3 3 3 3 4 4 4
[41] 4 4 4 4 4 4 4 5 5 6
> plot(xs)

0から6までの整数データを昇順にソートしたので、Index 1から50まで階段状に増加しています。

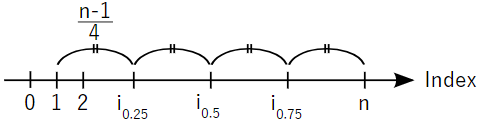
このソートしたデータxsのIndexを4等分する点を求めます。下図は、Index 1からnを4等分した点を示しています。

Index 1を0%、Index nを100%として、Indexを4等分する25%、50%、75%の点をそれぞれ$i_{0.25}$、$i_{0.5}$、$i_{0.75}$とします。4等分は (n - 1)/4 ですので¹、$i_{0.25}$、$i_{0.5}$、$i_{0.75}$はそれぞれ以下で表されます²。

$$ i_{0.25} = 1 + \frac{n - 1}{4} = \frac{n + 3}{4} $$

$$ i_{0.5} = 1 + 2 \cdot \frac{n - 1}{4} = \frac{n + 1}{2} $$

$$ i_{0.75} = 1 + 3 \cdot \frac{n - 1}{4} = \frac{3 n + 1}{4} $$

これらの式を用いて$i_{0.25}$、$i_{0.5}$、$i_{0.75}$をそれぞれRで計算します。

> n <- length(x)  # xの長さ(サンプルデータxの要素数)

> i25 <- (n+3)/4  # 25%点
> i25
[1] 13.25

> i50 <- (n+1)/2  # 50%点
> i50
[1] 25.5

> i75 <- (3*n+1)/4  # 75%点
> i75
[1] 37.75

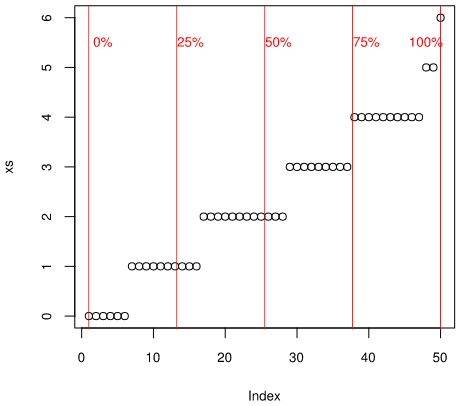
この4等分点からIndexを4等分する線をソートしたxの図に加えると下図になります。

> lines(c(1,1), c(-1,7), type="l", col="red")  # (1,-1)から(1,7)に赤い線を引け
> lines(c(i25,i25), c(-1,7), type="l", col="red")
> lines(c(i50,i50), c(-1,7), type="l", col="red")
> lines(c(i75,i75), c(-1,7), type="l", col="red")
> lines(c(n,n), c(-1,7), type="l", col="red")
> text(3, 5.5, "0%", col="red")  # (3, 5.5)に赤い字で25%と書け
> text(i25+2, 5.5, "25%", col="red")
> text(i50+2, 5.5, "50%", col="red")
> text(i75+2, 5.5, "75%", col="red")
> text(48, 5.5, "100%", col="red")

サンプルデータxの第一四分位数は、図4の25%線とデータxsが交差する点から求まります。同様に第二四分位数（中央値）は50%線との交点、第三四分位数は75%線との交点から求まります。

第一四分位数を計算します。

> i25f <- floor(i25)  # i25 = 13.25 以下の最大の整数を求めよ
> i25f
[1] 13
> qu1 <- xs[i25f] + (xs[i25f + 1] - xs[i25f]) * (i25 - i25f)  # 第一四分位数を計算せよ
> qu1
[1] 1

Rコードは変数で計算していますが、今回のサンプルデータのケースでは次の計算をしています。

$$ Q_1 = xs_{13} + (xs_{14} - xs_{13}) \cdot 0.25 $$

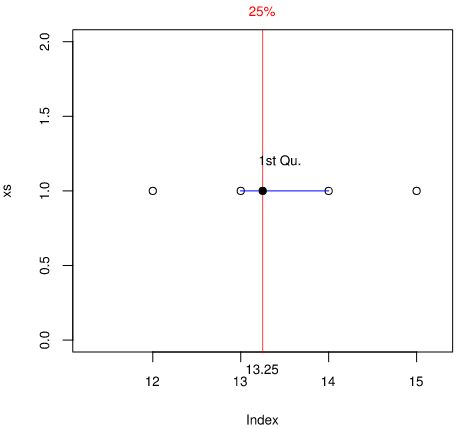
計算ををわかりやすくするために拡大した図を示します。

> plot(xs, xlim=c(i25-2,i25+2), ylim=c(0,2))
> lines(c(i25,i25),c(-1,7),type="l",col="red")
> lines(c(13,14),c(xs[13],xs[14]),type="l",col="blue")
> points(i25, qu1, pch=19)

> par(xpd=T)  # プロット領域外への描画を許可せよ
> text(locator(1), "1st Qu.")
> text(locator(1), "25%", col="red")
> text(locator(1), i25)

Index 1から50の25％は先に求めた$i_{0.25} = 13.25$ですので、Index 13と14の間にあります。赤線とIndex 13と14の要素を線形補間した青線との交点が第一四分位数です。このケースではxs[13]とxs[14]がどちらも1ですので、計算せずとも第一四分位数は$Q_1 = 1$です。

Indexの4等分線を加えた図から第二四分位数(中央値)は2になることが明らかですので、計算を飛ばします。

第一四分位数と同様に、第三四分位数を計算します。

> i75f <- floor(i75)  # i75 = 37.75
> i75f
[1] 37

> qu3 <- xs[i75f] + (xs[i75f + 1] - xs[i75f]) * (i75 - i75f)  # 第三四分位数を計算せよ
> qu3
[1] 3.75

具体的には次の計算をしています。

$$ Q_3 = xs_{37} + (xs_{38} - xs_{37}) \cdot 0.75 $$

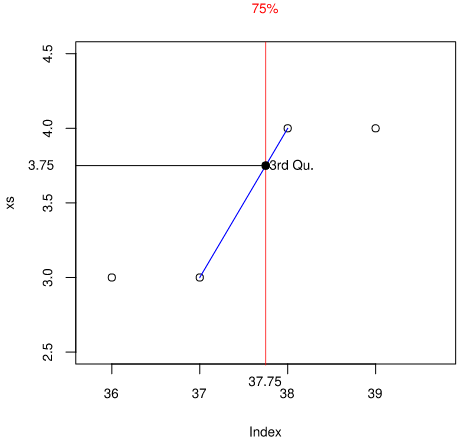
第三四分位数あたりを拡大したグラフを下図に示します。

Index 1から50の75％は先に求めた$i_{0.75} = 37.75$ですので、Index 37と38の間にあります。赤線とIndex 37と38の要素を線形補間した青線との交点が第三四分位数です。このケースでは$xs[37] = 3$で$xs[38] = 4$で両者に差があります。赤線と青線の交点を計算して、第三四分位数は$Q_3 = 3.75$ です。

summary関数で答え合わせ

第一四分位数（1st Qu.）と第三四分位数（3rd Qu.）を計算したので、summary関数の出力と比べてみます。

> qu1;qu3  # 自分で計算した 1st Qu. と 3rd Qu.
[1] 1
[1] 3.75
> summary(x)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
   0.00    1.00    2.00    2.34    3.75    6.00

両者は一致しています。

まとめ

Rでsummary関数やquantile関数などの組み込み関数を使わずに四分位数を計算しました。
随時グラフを書きながら、順を追って四分位数を計算しました。
最後に計算結果とsummary関数を比較して両者が一致していることを確かめました。

0からnを4等分するならばn/4ですが、1からnを4等分するので(n-1)/4となります。 ↩
内分点の公式を用いても同じことです。 ↩