包除原理とマンハッタン距離と二項係数【競技プログラミング】

はじめに

• 包除原理とマンハッタン距離と二項係数は、直接の関係はないけど、ある一つの問題を解くときに使った知識だから、まとめただけです。
• ちなみに、３つとも大した内容ではないです。言葉だけ聞くとすごい感じがするけどね。

包除原理とは

• wikiにも書いてあります。
• 例えば、下図のような集合が重なり合った図を見てもらえば、ぱっと頭に入ってくると思うけど、端的に言えば、集合の重ね合わせをしたときの、和集合の表現方法です。
  • それだと、ちょっと分かりづらい？ですよね～
  • 和集合を、和の記号（∨）を使わず、共通記号（∧）だけで表す方法です。
    
• 上記の集合AとBの和集合A∨Bを「∨」を使わず「∧」だけで表すと...
  • $A∨B ＝ A + B - A∧B$
    
• 続いて、A∨B∨Cについては、
  • $A∨B∨C ＝ ( A ＋ B ＋ C ) - ( A∧B ＋ B∧C ＋ C∧A ) ＋ ( A∧B∧C )$
• このように、和集合について、下記のように表すことができます。$(-1)^{k-1}$が注目ポイントかな。
  
• 「包除原理」はこれだけです。拍子抜けでごめんね。

マンハッタン距離とは

• wikiにも書いてあります。
  
• 上図の黒丸間の距離は、黒丸の座標を（x1,y1）と（x2,y2）としたとき、距離=|x2-x1|+|y2-y1|です。
  • 赤ルートでも青ルートでも黄色ルートでも同じ距離になります。
  • これをマンハッタン距離と呼びます。
• おわり
• 本当に、拍子抜けでごめん。

二項係数とは

• wikiにも書いてあります。
• でもまぁ、二項係数って$\binom{ n }{ k }$みたいな書き方して高尚な感じだけど、つまりはコンビネーション「${}_n\mathrm{C}_k$」と意味は同じで、$\frac{ n! }{ k! ( n - k )! }$のことです。
• おわり
  • といっても、これだけだと寂しすぎるから、有名な公式を書いておこうか。
  • $\binom{ n }{ k }$ = $\binom{ n }{ n-k }$
    • これは、直感でわかるよね。n個から「k個を選ぶ」ってことは、「n-k個を選ばない」ってことだから、組み合わせの数としては一致する。
  • $\binom{ n }{ k }$ = $\binom{ n-1 }{ k-1 }$ + $\binom{ n-1 }{ k }$
    • これはちょっと、直感ではわからないよね。
    • (特定のものAを含む）n 個のものから k 個のものを選ぶ組み合わせの数は、まず、①Aを選ぶ場合と②Aを選ばない場合の2つに分けた、下記の合計。
      • ①Aを選び、「残りn−1 個の中から r−1 個のものを選ぶ組み合わせの数」
      • ②Aを選ばず、「残りn−1 個の中から r 個のものを選ぶ組み合わせの数

学んだ知識で解く対象

• 問題：下記の「場合の数」を求めよ(mod 1000000007)
  • 縦H×横Wのマスを考える。
  • マスの座標について左上の角を(0,0)、右下の角を(H-1,W-1)とする
  • マス間の移動は、「右」「下」のみ進むことができる。
  • もし、上記条件のみだけだと、(0,0)から(H-1,W-1)へのルートの数は$\binom{H+W-2}{H-1}$となる。
  • しかし、N個のマスが与えられ、そこは「壁」となり、通れないマスとなる。
  • このときのルートの数を求めよ。
• 入力例

3 4 2 // H3 × W4 のマス、2個の壁
2 2 // 1つ目の壁：1-idx表示なので、0-idxにすれば、(1,1)
1 4 // 2つ目の壁：1-idx表示なので、0-idxにすれば、(0,3)

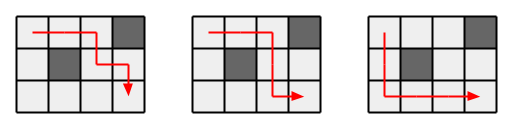
• 上記入力例の答えは、上図の通り3。

補足

• さっき、しれっと「(0,0)から(H-1,W-1)へのルートの数は$\binom{H+W-2}{H-1}$となる。」って書いたけど、理屈はわかってるかな？
• 2色のおはじきの並べ方って言えばわかるかな？
  • つまり、(0,0)から(H-1,W-1)へのルートの数って、つまり、「H-1個の赤いおはじき」と「W-1個の青いおはじき」の計(H+W-2)個のおはじきの並べ方の数と同じなんだよね。だから、$\frac{ (H+W-2)! }{ (H-1)!・(W-1)! }$。よって、$\binom{H+W-2}{H-1}$個だよ。
• ルート数を数える関数は何度も使うことになるから、仮置きでc(a,b) = $\frac{ (a+b)! }{ a!・b! }$と定義しておこう。ちなみにcはコンビネーションのcだよ。ここでは、二項係数が登場したね。

問題の解き方（初歩）

• 壁がゼロのときのルートの数$\binom{H+W-2}{H-1}$を出発点として、壁を通るルートを削って求めよう。
  
• 例えば、上図のような青い部分が壁であれば、以下のように考えます。
  • 壁がゼロのときのルートの数をSGとすると、SG=c(H-1,W-1)
  • 壁Aを通るルートの数をR(A)とすると、R(A)=c(h0,w0)×c(H-1-h0,W-1-w0)、同様に、R(B)、R(C)も計算できるね。
  • でも、当然だけど、答えはSG-(R(A)-R(B)-R(C))ではないよ。
  • 壁A,Bの２つを通るルートの数をR2(A,B)とすると,
    • R2(A,B)=c(h0,w0)×c(h1-h0,w1-w0)×c(H-1-h1,W-1-w1)
  • 壁A,B,Cの３つを通るルートの数をR3(A,B,C)とすると、
    • R3(A,B,C)=c(h0,w0)×c(h1-h0,w1-w0)×c(h2-h1,w2-w1)×c(H-1-h2,W-1-w2)
  • 答えは、SG - (R(A)-R(B)-R(C)) + (R2(A,B)+R2(B,C)+R2(C,A)) - R3(A,B,C)になるね。
  • ここで、包除原理が登場したね！
    
• それでは、上図ではどうだろうか？移動は、「右」か「下」にしかいかないから、R2(A,B)はゼロになるように計算しないといけないね。当然、R3(A,B,C)もゼロだね。
  • その前提で考えれば、答えはやはり、
  • SG - (R(A)-R(B)-R(C)) + (R2(A,B)+R2(B,C)+R2(C,A)) - R3(A,B,C)になるね。
• うむ！計算量を無視すれば、上記ロジックで計算可能だね！
• あれ？まだ、マンハッタン距離を使ってないぞ？
• ああ、そうだった。壁の位置関係でマンハッタン距離を使うんだった。
• スタート地点Sから壁Aのマンハッタン距離をD(S,A)とすると、D(S,A) = h0 + w0だね。
  • 壁Aから壁Bへのルートが有るとき、必ず、D(S,A)<D(S,B)の関係となっている。
    • 言うまでもないけど、D(S,A)<D(S,B)だからといって、壁Aから壁Bへのルートがあるわけではないよ。
  • だから、問題で壁の位置を与えられたあと、スタート地点からのマンハッタン距離の短い順でソートしておきましょう。これで、マンハッタン距離も拾ったね！
• あと、コンビネーションの関数をc(a,b)としてたけど、一般的にはcomb(n,k) = $\frac{ n! }{ k!・(n-k)! }$を使うよ。以下の説明では、combを使うよ。

コードを書く

• 前記の考え方に基づき、コードを書こうと思うけど、経由地の壁が増えるたびに、R,R2,R3と別の関数を作るのはアホっぽいよね。だから、そんなことはしないよ。というか、この問題は「教育的DP問題」のひとつなので、最初からdpを使って解くのは決まっているのでした。
• また、制約では、$N<3000$となっているから、$O(N^2)$はOK!。$O(N^2･logN)$は厳しいかも...$O(N^3)$は確実にアウト。
• そして、dpを考えるけど、素直に考えると、こんな感じ
  • dp[i][j] ：j個の壁を通って壁i-1にたどり着くルートの数
  • ここで、jは壁i-1自身の個数を含まない。つまり、スタート後に最初にあたる壁がi-1となるルートの数は、dp[i][0]となる。
    • このとき、途中で１つ以上の壁を通って、ゴールに辿り着くルートの数は、ゴール(H-1,W-1)をN+1個目の壁(0-idxではN番目の壁)と考えたとき、
      • DP[N+1].enumerated().map{$0 % 2 == 0 ? $1 : -$1 }.reduce(0,+) となる
        • map関数により、配列のインデックスの偶奇で値の正負を入れ替える。
        • reduce関数により、配列の合計値を計算する。
      • おや？[j]って、偶奇判断にしか使ってなくない？
        • なら、dp[i][0/1]にすれば、計算量が減らせるね！
• dp[i][0/1]をつかって解くと、こんな感じです。

extension Array { // 初期化の省略記法のため
    init(_ cnt: Int, _ v: Element) {
        self = [Element](repeating: v, count: cnt)
    }
    init<T>(_ cnt2:Int, _ cnt1:Int, _ v:T) where Element == [T] {
        self = [[T]](cnt2,[T](cnt1,v))
    }
}

let (H,W,N) = [readLine()!.split(separator:" ").map{Int($0)!}].map{($0[0],$0[1],$0[2])}[0]
let start = (0,0) // スタート地点
let goal = (H-1,W-1) // ゴール地点
var rcs:[(Int,Int)] = []
for _ in 0..<N {
    let rc = [readLine()!.split(separator:" ").map{Int($0)!}].map{($0[0]-1,$0[1]-1)}[0]
    rcs.append(rc)
}
rcs.append(start)
rcs.append(goal)

let mod = 1000000007

rcs.sort{ $0.0+$0.1 < $1.0+$1.1 }

func comb(_ n:Int,_ k:Int)->Int{

    var c = n
    var a = k
    var b = n-k

    var ans = 1
    while c>1 { ans *= c ; c-=1 } // ①
    while a>1 { ans /= a ; a-=1 } // ②
    while b>1 { ans /= b ; b-=1 }
    
    return ans
}

// 壁aから壁bに対して、ルートがあれば、ルートの数、なければ0を返す
func rt(_ a:Int,_ b:Int)->Int{
    if a == 0 && b == N+1 {return 0} // スタートからゴールへ直で行くルートは除く
    let dh = rcs[b].0 - rcs[a].0
    let dw = rcs[b].1 - rcs[a].1
    if dh < 0 || dw < 0 {return 0} // ルートがないときは除く
    return comb(dh+dw,dw)
}

var dp = [[Int]](N+2,2,0) // 初期値はdp[0][1]=0のみ意味がある（他は全て塗り替えられる）

//初期値
dp[0][0] = 1

for i in 1..<N+2 {
    for eo in 0...1 { // 偶奇even-oddの意味でeo
        var sum = 0
            for old in 0..<i {
                sum += dp[old][eo] * rt(old,i)
            }
        dp[i][1 - eo] = sum // eo反転して反映
    }
}

print(comb(H+W-2,H-1) - dp[N+1][0] + dp[N+1][1])

• ここまでは、余裕かな？
• でも、このコードって、comb関数がmod対応も計算量も完全無視したアホ仕様だけどね。
• メイン部分のループは３重ループだけど、for-eoは2回しか回さないから、実質$O(N^2)$になってる...かのように見えるけど、rt関数に含まれるcomb関数がO(H+W)の計算量になっているから、トータルで$O((H+W)･N^2)$の計算量になるから、ダメ。
• comb関数のmod対応と高速化については、別投稿(初級編、中級編、上級編)で説明しているから、そっちを見て欲しい。
• ここで解説しないけど、mod適用した関数combは以下のとおり。前処理として、O(H+W)の計算を行っているけど、メイン部分のループでの処理に含まれないので、全体としては、$O((H+W)+N^2)$になってるはず！

class Comb {
    let mod:Int
    var fac:[Int] // 階乗計算結果
    var inv:[Int] // 逆数計算結果
    var finv:[Int] // 逆数の階乗計算結果
    
    init(mod:Int,max:Int){
        self.mod = mod
        let MAX = max + 1
        
        fac = [Int](repeating: 1, count: MAX)
        inv = [Int](repeating: 1, count: MAX)
        finv = [Int](repeating: 1, count: MAX)       
        
        for i in 2..<MAX {
            fac[i] = fac[i-1] * i % mod
            inv[i] = mod - (mod / i) * inv[mod % i] % mod
            finv[i] = finv[i-1] * inv[i] % mod
        }
        
    }
    
    func comb(_ n: Int, _ k: Int) -> Int {
        fac[n] * finv[k] % mod * finv[n - k] % mod
    }

}

let comb:(Int,Int)->Int = Comb(mod:mod,max:200000).comb

• さて、上記のシンcomb関数を使って、rt関数以降を下記の通り、書き換えて最終化した。

func rt(_ a:Int,_ b:Int)->Int{
    // if a == 0 && b == N+1 {return 0} // 変更：スタートからゴールへ直で行くルートを除くの止めた！
    let dh = rcs[b].0 - rcs[a].0
    let dw = rcs[b].1 - rcs[a].1
    if dh < 0 || dw < 0 {return 0}
    return comb(dh+dw,dw)
}

var dp = [[Int]](N+2,2,0)


dp[0][0] = 1

for i in 1..<N+2 {
    for eo in 0...1 {
        var sum = 0
        for old in 0..<i {
            sum = (sum + dp[old][eo] * rt(old,i) % mod) % mod // 変更：mod対応させただけ！
        }
        dp[i][1 - eo] = sum
    }
}

print((dp[N+1][1] - dp[N+1][0] + mod) % mod) // 変更：dp[N+1][1]にスタートからゴールへ直で行くルートを含めて、mod対応

• 上記コードで提出したら100ms程度でAC。

おわりに

• 最初は、楽勝問題かな？と思っていたけど、二項係数のmod対応が意外と大変だったよ。
• まぁ、過去のmodに関する投稿を再確認できたのは、良い復習になりました。