はじめに
この記事ではディープラーニングの入門について書いていきます。社内勉強会用の発表資料も兼ねてます。
前提知識として、基本的なニューラルネットワークのモデルを理解していることを方向けに書いています。
ディープラーニング(深層学習)とは
ニューラルネットワークの基礎として、入力層と出力層のみのモデルでは、ニューラルネットワークのモデルは線形分離しかできませんでした。
しかし、隠れ層を増やすことにより非線形分離ができるようになります。
より複雑なパターンを認識・分類するためには次の2つのアプローチが考えられます。
- 隠れ層のにあるニューロン数を増やす
- 隠れ層自体の数を増やす
特に、後者のアプローチをとることによりニューラルネットワークの層は深くなるが、そうした深い層を持つネットワークのことをディープニューラルネットワークと呼ぶ。
そしてこのディープニューラルネットワークを学習する手法のことを総じてディープラーニングあるいは深層学習と呼びます。
しかし、だた単純に隠れ層の数を増やすだけではうまくいかないのが現実問題としてあります。
この記事ではその原因を明らかにし、どうすれば解決できるかを考えます。
学習における問題
勾配消失問題
まず、1つ目の原因として勾配消失問題が挙げられます。
モデルの学習では、最適解を求めるために各パラメータの勾配を求める必要があったが、勾配消失問題は、文字通りこの勾配が消えてしまう(=0になってしまう)問題のことをいいます。
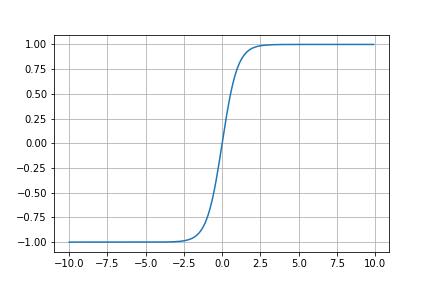
活性化関数がシグモイド関数$\sigma( \cdot )$の場合についてこれを考察してみます。
シグモイド関数の導関数は、
$$
\sigma'(x) = \sigma(x)(1 - \sigma(x))
$$
で表されました。
ひとまずこれを証明してみます。
$$
\sigma(x) = \frac{1}{1 + \exp(-x)} = (1 + \exp(-x))^{-1}
$$
であるので、
$$
\begin{align}
\sigma'(x) &= -(1 + \exp(-x))^{-2} \cdot (-\exp(-x)) \\
&= \frac{\exp(-x)}{(1 + \exp(-x))^2} \\
&= \frac{1}{1 + \exp(-x)} \cdot \frac{\exp(-x)}{1 + \exp(-x)} \\
&= \sigma(x)(1 - \sigma(x))
\end{align}
$$
と示されます。
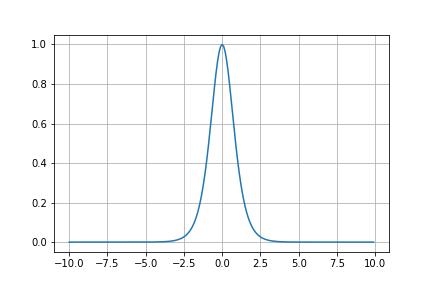
この導関数をグラフで見てみると・・・
$x = 0$のとき最大値$\sigma'(0) = 0.25$をとります。
これが意味するのは、隠れ層の数が$N$の場合、誤差逆伝播により$A_n \leq 0.25^N$なる係数$A_n$が誤差を計算する上でかかってくるということです。
そのため隠れ層の数が増えるにつれ誤差項の値が急速に0に近づいていってしまうという問題が発生します。
これが勾配消失問題の原因です。
この問題を回避するには、「微分しても値が小さくならない活性化関数」を考えるといった対策が必要となります。
そこであとで様々な活性化関数を見ていきたいと思います。
オーバーフィッティング問題
勾配消失問題に加え、もう一つ大きな問題となるのがこのオーバーフィッティングです。
これは過学習あるいは過剰適合とも呼ばれるが、文字通り「データを学習しすぎた」状態になってしまうことを言います。
実験において、訓練データに対しての予測はうまくいくのに、テストデータはうまく予測できないという場面に遭遇した場合、まずオーバーフィッティングを疑うのがよいでしょう。
上記問題の解決
ディープラーニングは、ネットワークを深層にする際に生じる問題を解決するテクニックの積み重ねです。
上の勾配消失問題にせよ、オーバーフィッティング問題にせよ原因はわかっているのであとはそれにどう対処すればよいか考えるだけです。
その1つ1つは決して難しいものではないので、順番に理解していくことが大切です。
さまざまな活性化関数
シグモイド関数を用いることで勾配が消失してしまうのであれば、別の活性化関数を用いることでこの問題を回避できないか考えてみます。
多層パーセプトロンのモデル化と同様、出力層における活性化関数は確率を出力する関数でなければならないので、通常シグモイド関数あるいはソフトマックス関数が用いられます。
ですが、隠れ層における活性化関数は、「受け取る値がちいさければ小さい値を出力し、受け取る値が大きければ大きい値を出力する」関数であれば理論上問題はありません。
それに当てはまる関数をこれから見ていきます。
- 双曲線正接関数(ハイパボリックタンジェント)
$$
\tanh(x) = \frac{\sinh(x)}{\cosh(x)} = \frac{\exp(x) - \exp(-x)}{\exp(x) + \exp(-x)}
$$
グラフで見ると・・・
見た感じシグモイド関数と形が似ています。
導関数の式とグラフは
$$
\tanh'(x) = \frac{1}{\cosh ^2(x)} = \frac{4}{(\exp(x) + \exp(-x))^2}
$$
となるので、シグモイド関数の導関数$\sigma'(x)$が最大値$\sigma(0) = 0.25$であったのに対し、$\tanh'(x)$は$\tanh'(0) = 1$が最大値となるので、シグモイド関数と比べ勾配が消失しにくいことがわかります。
導関数のグラフの形もシグモイド関数とそっくりですね。
- ReLU
双曲線正接関数を用いることで勾配は消失しにくくなるが、シグモイド関数と同様、関数の中身の値が大きくなる場合は勾配が消えてしまうという問題が依然としてありました。
そこでReLU(rectified linear unit)が用いられるようになりました。
これは式では以下のように表されます。
$$
f(x) = \max(0, x)
$$
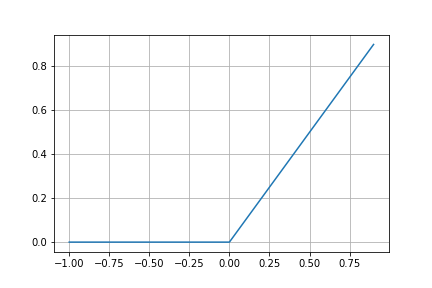
描写してみます。
import numpy as np
import matplotlib.pyplot as plt
def relu(x):
return np.maximum(0, x)
x = np.arange(-1, 1, 0.1)
# 描写
plt.plot(x, relu(x))
plt.grid()
plt.savefig('relu.png')
導関数は、
f'(x) = \left\{
\begin{array}{ll}
1 & (x \gt 0) \\
0 & (x \leq 0)
\end{array}
\right.
となり、ステップ関数の形をしていることがわかります。
ReLUの導関数はxがどんなに大きくなっても1を返すので、勾配が消失することはありません。
一方、$x \leq 0$のときは関数の値も勾配も0となるので、ReLUを活性化関数に用いたネットワーク内のニューロンは、一度不活性になると、学習の間中ずっと不活性のままといったことが起こりえます。
- Leaky ReLU
Leaky ReLU(LReLU)は、ReLUの改良版と言える関数で、以下の式で表されます。
$$
f(x) = max(\alpha x, x)
$$
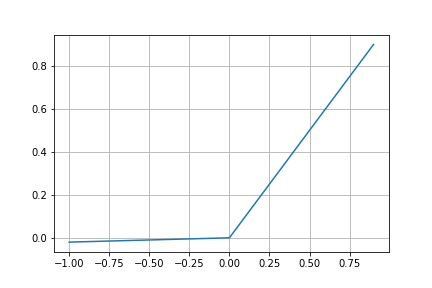
ここで、$\alpha$は0.01など小さい定数を表します。
ReLUと違い$x \leq 0$に傾きが見られます。
グラフを見ればわかるように導関数は、
f'(x) = \left\{
\begin{array}{ll}
1 & (x \gt 0) \\
\alpha & (x \leq 0)
\end{array}
\right.
となります。
ReLUは$x \lt 0$のときに勾配が消えてしまうので、学習が不安定になり得るという問題がありましたが、LReLUは$x \lt 0$でも学習が進むので、ReLUよりも効果的な活性化関数として期待されました。
しかし、実際には効果が出るときもあれば出ないときもあり、どのようなときに効果がでるのかについては、まだはっきりとはわかっていないのが現状です。
ドロップアウト
これは上のディープニューラルネットワークを学習する際の問題の内、オーバーフィッティングを防ぐ方法です。
方法はとてもシンプルで名前の通り、学習の際にランダムにニューロンをある確率$p$で「ドロップアウト(=除外)」させるものです。
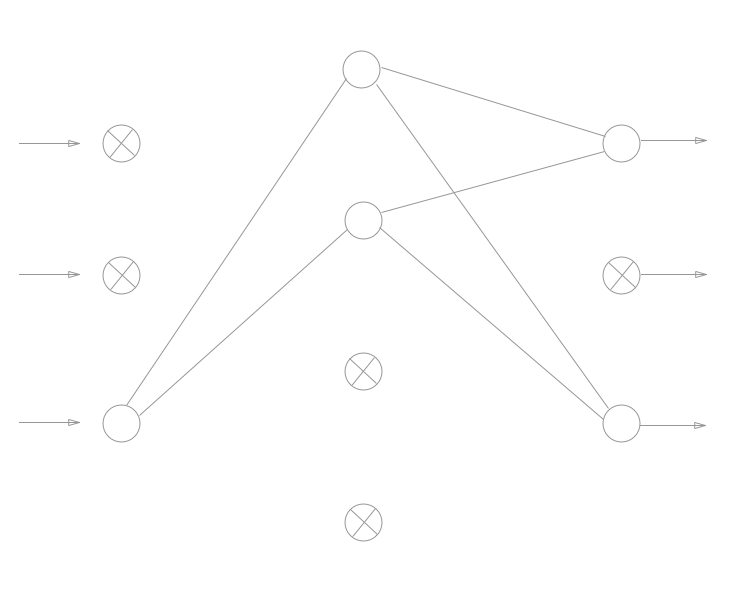
イメージ的には以下の図のような感じです。
✕印がついたニューロンがドロップアウトを適用したニューロンであり、これらはあたかも「ネットワーク上に存在しないもの」として扱われます。
なぜ、ドロップアウトで汎化性能が向上するかは、ドロップアウトを適用することによって、実質的にたくさんのモデルを生成・学習し、それらの中で予測を試みているからと考えるわかりやすいかもしれません。
ドロップアウトは擬似的にランダムフォレストのようなアンサンブル学習を行っていることになります。
おわりに
今回はディープラーニングの理論についてやってきました。
のちのち実装中心の記事を書きたいと思います。